Asymptotic Notations[알고리즘]

Asymptotic Notations (점근적 표기법)

Asymptotic Notations는 알고리즘의 running time을 설명하기 위해 사용한다.
예를들어, bubble sort에서는 이미 정렬되어 있을경우에는 best case 이지만
거꾸로 정렬되어 있다면, worst case이다.
정렬도 되어있지 않고, 거꾸로 되어있다면 , average time이다.

이러한 경우들을 표기 위한것이 asymptotic notation이다.
이것들에는 세가지 종류가 존재한다.

• Big-O notation
• Omega notation
• Theta notation

Big-O Notation

big-O는 알고리즘의 upper-bound를 나타낸다. 즉, 작거나 같은 값을 말한다.

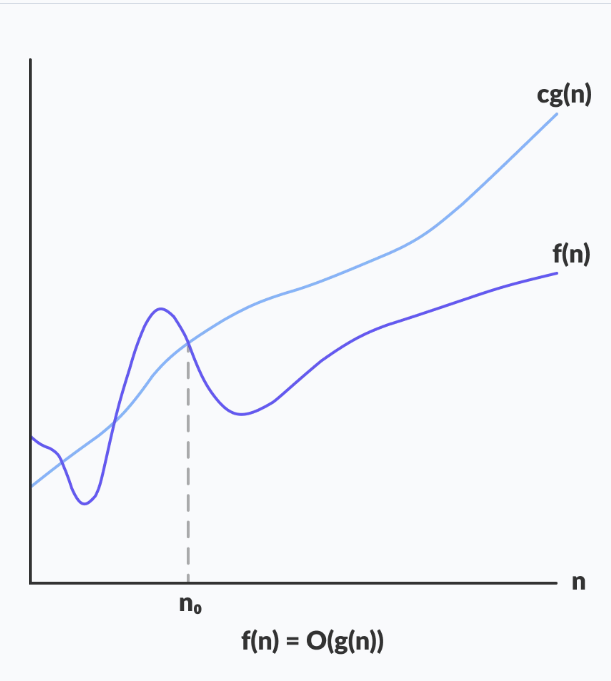
위 그림을 보면 n > n0 인 경우에 f(n)이 cg(n) 보다 작다.
이것을 식으로 나타내면 다음과 같다.
0 <= f(n) <= cg(n) for all n >= n0 }

알고리즘의 running time은 O(g(n))에서 제공한 시간을 넘어가지 않는다.

Big-O는 worstcase를 나타낼때 사용된다.

Omega Notation(Ω-notation)

Omega는 algoritm의 running time의 lower bound를 나타낸다.
그래서 Omega는 best case의 time complexity를 알려준다.

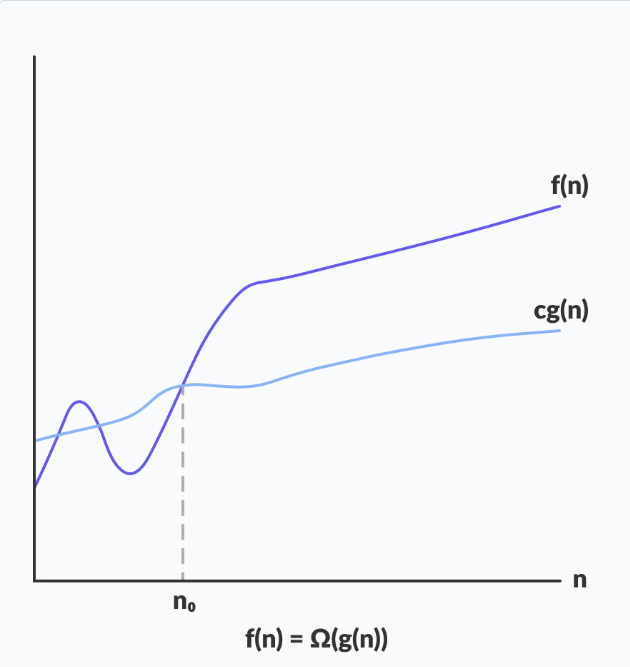
위 그림은 n >= n0 일때 f(n)이 cg(n) 보다 항상 큰것을 알 수 있다.
0 <= cg(n) <= f(n) for all n>=n0

Theta Notation(Θ-notation)

Theta는 알고리즘 running time의 lower bound 와 upper bound를 모두 나타낸다. 때문에 average-case complexity를 나타낸다.

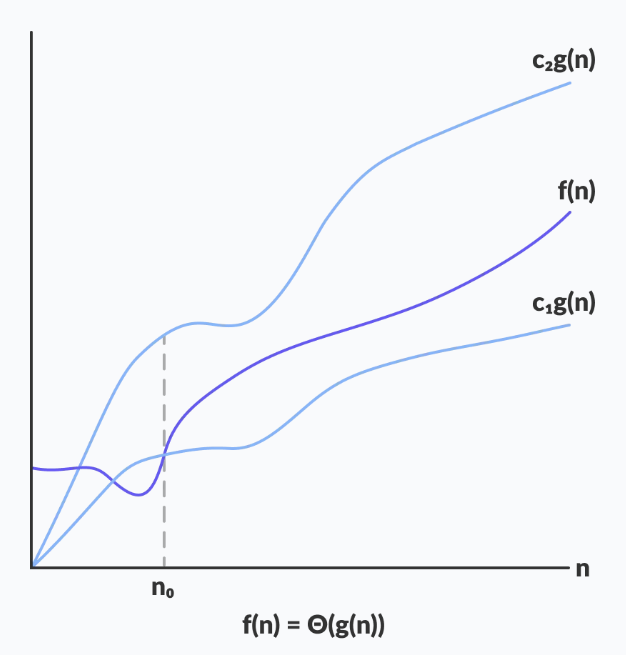
0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0

유용한 합계 공식

모두 i=1부터 n까지 더함
$\sum_{i=1}^{n} 1$= 1+1....+1 = n
$\sum_{i=1}^{n} i= 1+2+3+4+.....+n$ = $\frac{n(n+1)}{2}$
$\sum_{i=1}^{n} i^2$= $1^2+2^2+3^2+....n^2$=$\frac{n(n+1)(2n+1)}{3}$

example

예제1

for i<-0 to n-2 do
	for j <-i+1 to n-1 do
    	if A[i] = A[j] return false
return true

worst-case
A[i] = A[j]가 없음
배열의 가장 마지막에 A[i] = A[j]가 있음

$C_{worst}(n)$=$\sum_{i=0}^{n-2} \sum_{j=i+1}^{n-1} 1 =\sum_{i=0}^{n-2} (n-1)-(i+1)+1$=$\sum^{n-2}_{i=0} n-1-i$

= $\sum_{i=0}^{n-2} (n-1)-\sum_{i=0}^{n-2} i$
= $(n-1)\sum_{i=0}^{n-2} 1-\frac{(n-2)(n-1)}{2}$
= $(n-1)^2-\frac{(n-2)(n-1)}{2}=\frac{(n-1)n}{2}$
$\approx\frac{n^2}{2}\in\theta(n^2)$

또는

$\sum^{n-2}_{i=0} n-1-i$ = $(n-1)+(n-2)+....(1)=\frac{(n-1)(n)}{2}$
$\approx \frac{n^2}{2}=\theta(n^2)$

예제2

MatrixMultiplication(A[0...n-1,0...n-1],B[0...n-1,0...n-1])

n by n인 두개의 행렬 A,B를 곱한다.

for i<-0 to n-1 do
	for j<-0 to n-1 do
    	C[i,j]<-0,0
        for k<-0 to n 1do
        	C[i,j]<-C[i,j]+A[i,k]*B[k,j]
return c

$M(n) = \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}\sum_{k=0}^{n-1} 1=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1} n=\sum_{i=0}^{n-1}n^2=n^3$