computer system stack

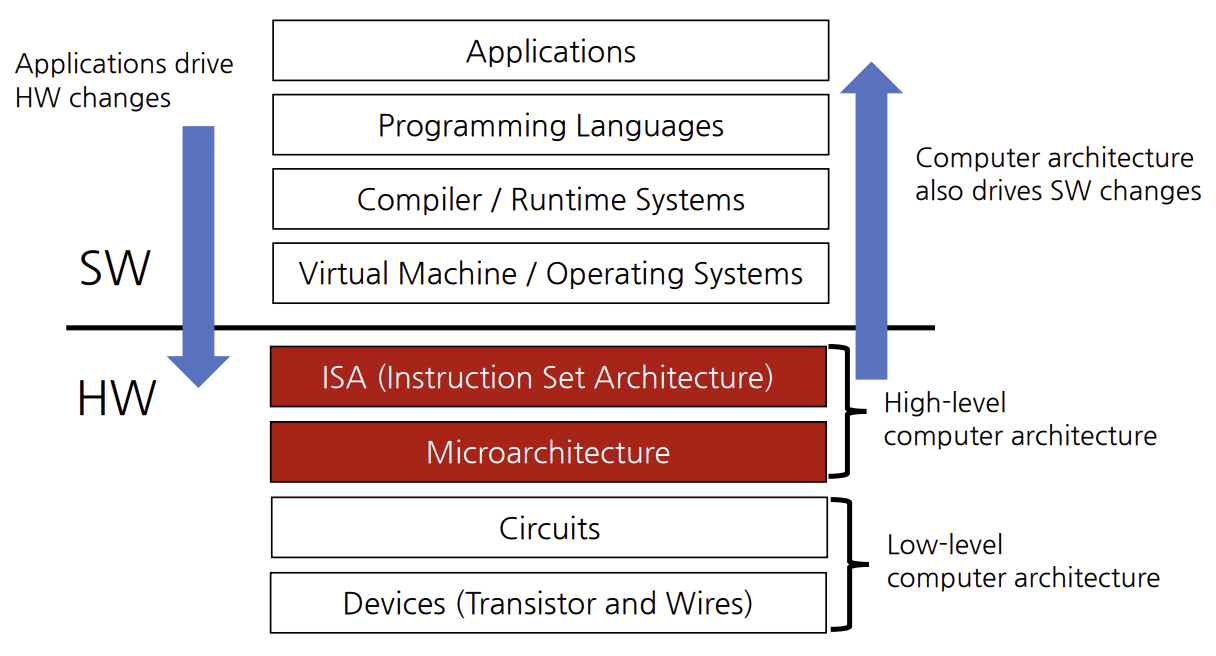
• ISA
  • 명령어 집합구조이다.
  • HW와 SW사이에 인터페이스 역할을 한다.
  • 호환성 때문에 변화를 잘 안한다.
  • 다양한 ISA가 존재( e.g)x86,ARM,SPARC,MIPS.....)
• Microarchitecture
  • 일종의 컴퓨터 설계도
  • GPU,CPU 같은 프로세서(I/O subsystems 포함)들의 작동방식 서술

컴퓨터 하드웨어 동작

Instruction Set

• 다른 컴퓨터에서는 다른 instruction set을 가진다.
  (대부분은 같다.)
• 빠른 컴퓨터는 instruction set이 심플하다.
• 현대 컴퓨터들은 심플한 instruction set을 가진다.
• 임베디드에서 많이 쓰인다.(가전제품,네트워크 장비,카메라,프린터 등등)
• 2002년에 거의 100만개에 달하는 MIPS 프로세서들이 제조되었다.

Arithmetic Operations

• add a, b, c // a = b + c
  sub a, b, c// a = b - c
  대부분의 arithmeic 연산은 이 형식을 따른다.
• 중요한건, 심플하게 만들어야 적은 비용으로 더 높은 퍼포먼스를 낼 수 있다.

Arithmetic Example

f  = (g + h) - (i + j);
// MIPS code
add $t0,g,h #temp to = g + h
add $t1,i,j #temp t1 = i + j
sub f,$t0,$t1 #temp f = (g + h) - (i + j)

Register Operands

• MIPS는 32개의 register로 구성되며, 각 register는 32 bit이다.

• register에 data를 올려 놓으면, 메모리에 접근할 필요가 없어서 data에 접근하기가 빠르다.

• registersms 0~31까지 있다.

• 32비트의 data를 "word"라고 부른다.

• Assembler

  • $t0,$t1,.....,$t9 for temporary values
  • $s0,$s1,.....,$s7 for saved variables
  • logic을 구성할때,최대한 instruction수를 적게 만들어야 빠르다.
  • $s는 8개인데, 만약 9개 이상의 변수를 사용하게 되면 어떻게 해결할까??
    • 가장 오래된 register를 메모리에서 내려 놓는다.

• arithmetic operation을 하기위해서
  메모리에서 register로 값을 가져온다.
  register에서 memory로 결과값을 저장한다.

memory Operand Example

example 1

c code

g = h + A[8];

여기서 g는 변수를 저장하는 레지스터인$s1 안에 h는 $s2안에 &A[0]는 $s3안에 저장된다.
A[8]에 해당하는 메모리를 확보하기 위해서는

lw $t0,32($s3) // load word

이렇게 해줘야 한다. $s3 레지스터로 부터 32만큼 떨어진 주소를 t0에 load 하겠다는 뜻이다. 이후에는 이렇게 식을 만들어 준다.

add $s1, $s2, $t0 // g = h + A[8] 

example 2

c code

A[12] = h + A[8];

이러한 경우, h는 $s2에 base adress인 A는 $s3에 저장된다.

MIPS code

lw $t0, 32($s3) // load word
add $t0, $s2, $t0 // s2와 t0를 더해서 다시 t0에 덮어쓴다.
sw $t0, 48($s3) //t0를 s3으로부터 48 떨어진 주소에 저장한다.

register vs memory

• 레지스터가 메모리보다 접근이 빠르다.
• 이유는, 메모리에 접근하기 위해서는 lw sw를 사용해야 해서 instruction이 더 많이 필요하다.
• 컴퓨터가 갖고 있는 레지스터보다 프로그램에서 사용하는 변수가 더 많은 경우가 있다. 이러한 경우에도 에러가 나지는 않는다. 왜일까?
  컴파일러는 자주 사용하는 변수를 레지스터에 가능한 많이 레지스터에 넣고 나머지 변수는 메모리에 저장했다가 필요할때만 꺼내쓴다.
  자주 사용하지 않는 레지스터를 메모리에 넣는것을 spilling 이라고 한다.

Memory hierarchy

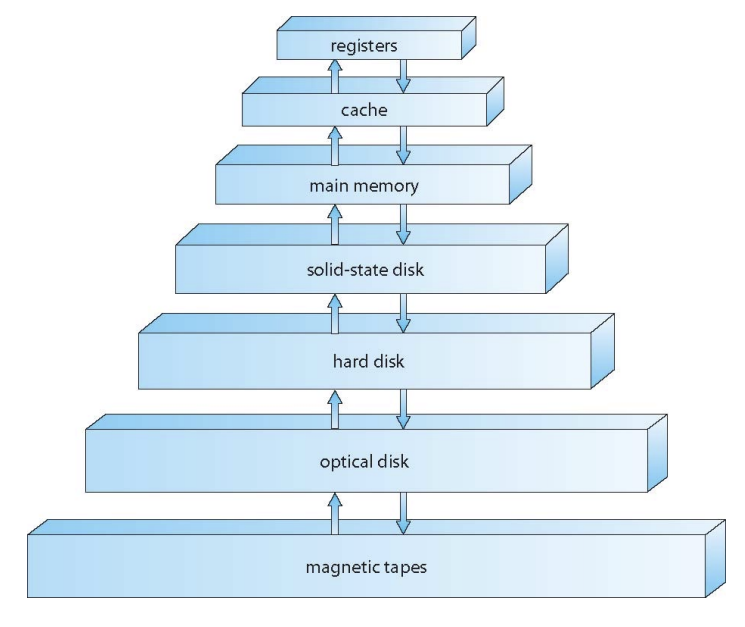
위로 올라갈수록, 접근성이 좋아 빠르고 공간은 적다.

Immediate Instructions

• 상수와 함께 계산하는 instruction 타입, I타입이라고 한다.
  addi $s3, $s3, 4 // constant data인 4를 s3와 더해서 s3에 저장

• I 타입에는 sub가 없다.
  addi $s2, $s2, -1 이런식으로 사용

• 상수 연산을 사용하면 메모리에서 데이터를 로드해오는 것보다 빠르다.

constant

• $zero는 항상 상수0이다.
• 상수 0은 유용한 여러 변형을 제공해서 단순한 명령어 집합을 가능하게 한다.
• 예를들어, 복사(move)연산은 피연산자 중 하나가 0($zero) 인 add 명령어이다.

Signed and Unsigned Operands

unsigned binary integers

• n- bit number의 범위는 0 ~ $2^n$ - 1

complement Signed integers

• n- bit number 범위 $- 2^{n-1}$ ~ $2^{n - 1}-1$

• 맨 왼쪽 비트가 1이면 negative 아니면 positive이다.

• 32비트 binary에서
  0: 0000 0000 ... 0000
  -1: 1111 1111 ... 1111
  Most-negative: 1000 0000 ... 0000
  Most-positive: 0111 1111 ... 1111

• 이러한 결과가 나오는이유는
  1111 1111 ... 1111 = 1$\times$$-2^{31}$ + 1$\times$$2^{30}$ +....+1$\times$$2^0$ 으로 계산하기 때문

• 비트 음수 만들기
  보수 취해준뒤 +1
  x + $\bar{x}$ = 1111 1111 ... 1111 = -1
  $\bar{x}$ + 1 = -x

예를들어
+2 = 0000 0000 ... 0010
보수 취해주면
1111 1111 ... 1101
여기다 +1
-2 = 1111 1111 ... 1110

sign Extension

• 8비트를 16비트로 확장 시키기(16비트 32비트로 확장도 원리는 같음)
• +2 = 0000 0010
  가장 상위 비트0을 왼쪽으로 8번 복사한후 원래있던 8비트는 뒤에 붙혀준다.
  -> 0000 0000 0000 0010
• -2 = 1111 1110 -> 1111 1111 1111 1110

MIPS-32 ISA

R-format

I-format

I타입이 만들어진이유는 R타입에서 만약에 lw같은 메모리 로드 instruction을 쓴다고 생각해보자. lw는 두개의 레지스터와 상수가 필요하다. 만약에 상수자리에 R-format에 있는 레지스터중 하나를 사용한다고 했을때 32보다 작은 값만 사용할 수 있다. 메모리가 큰 배열에서는 32비트는 부족하다. 따라서, 16비트를 사용할 수 있는 I 타입이 생긴것이다.

J-format

address 에는 절대주소 대신 word 단위로 바꾼다.
예를들어
Loop:sll $t1, $t3, 2
add $t1, $t1, $s6
.....
j Loop

가 있는데 Loop 레이블의 절대주소가 80000이라고 하면
j instruction의 Loop에는 20000이 들어가야한다.

Logical Operations

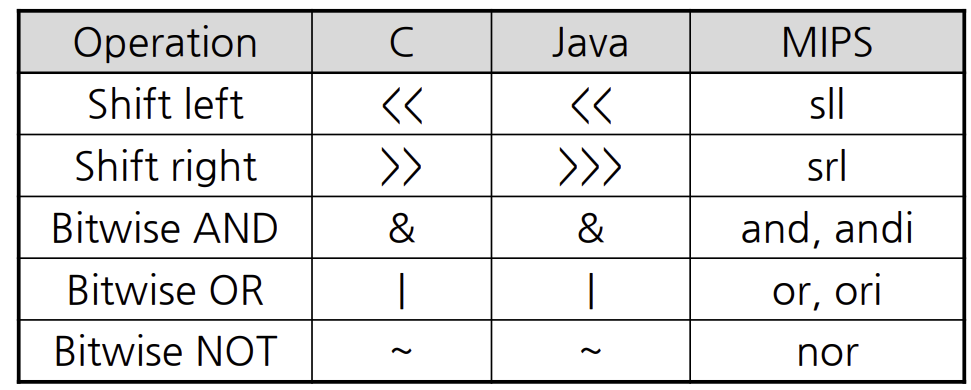
shift Operations

• shamt: shift 하고 싶은 값을 넣는다. 예를들어, 4번 shift하고 싶으면 00100을 shamt에 넣으면 된다.
• 만약 $s0 라는 레지스터에 0000 0000 .... 1001 = 9 가있었는데 4번 shift 해주면 0000 0000 .... 1001 0000 = 144가 된다.
  shift해주고 난 다음 빈공간은 0으로 채워준다.
  -sll은 한칸에 2씩 곱해주고, srl은 한칸에 2씩 나눠준다.

AND Operations

둘다 1이면 1 아니면 0을 t0에 넣어준다.

OR Operations

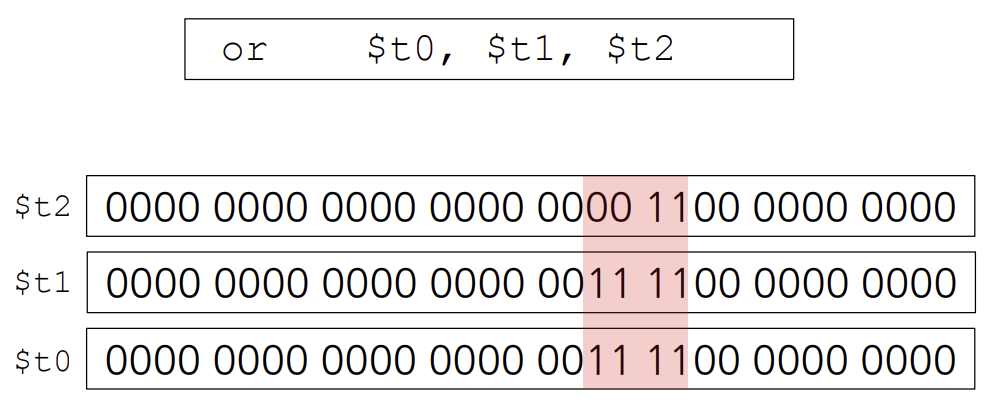
하나라도 1이면 1 아니면 0을 넣어준다.

XOR Opeartions

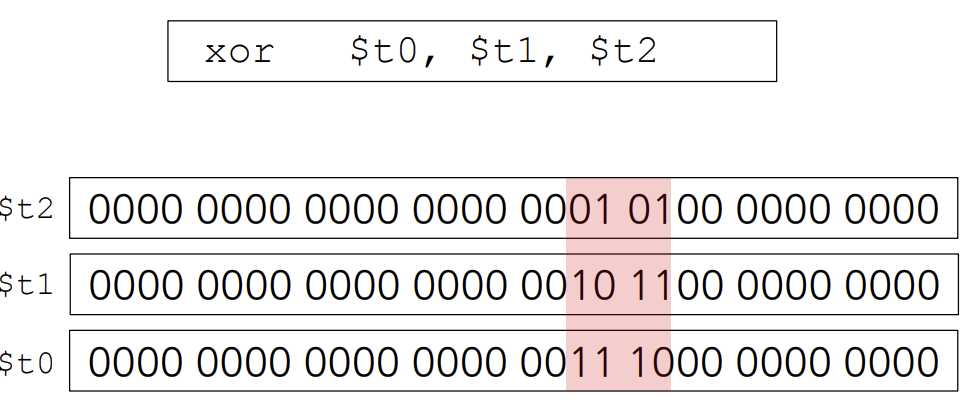
값이 같으면 0 다르면 1을 넣어준다.

NOT Operatinos

0과 1을 서로 바꾼다.

Conditional Operations

example

if(i == j) f = g + h; else f = g- h;

f,g,h,i,j를 각각 $s0~4에 할당되었다면 컴파일한 코드는??

i = j 라서 beq를 쓰면 될 것 같지만 실제로는 bne가 더 효율적이다.

bne $s3, $s4 Else // go to Else if(i != j)

add $s0,$s1,$s2 // f = g + h

j Exit

Else: sub $s0,$s1,$s2 // f = g - h(skipped if i != j)
Exit:

example 2

while (save[i] == k)
 i += 1;

컴파일하면,

i -> s3, k->s5, save->s6에 할당되었다면

Loop: sll $t0, $s3, 2 // t0 = i*4 
add $to,$to,$s6
lw $t1, 0($t0) 	// t1 = save[t0]
bne $t1, $s5, Exit // save[i] != k ->Exit
$addi $s3,$s3,1 // i += 1
 j Loop // go to Loop
Exit:

컴퓨터에서 곱하기 연산은 오래 걸리기 때문에 bit shift 연산이 더 효율적

slt slti

• slt(set on less than)와 slti는 조건이 참이면 1 아니면 0을 반환한다.
  보통 beq bne랑 같이 쓰인다.
  두 변수 간의 대소 비교가 필요할때가 있다. 예를들어서, for문에서 인덱스 변수 값이 0 보다 작은지를 검사할 때가 있다. 인덱스 변수가 0 보다 작으면 0을 반환하고 bne가 0과 다르기 때문에 루프를 빠져나가도록 해준다.

• blt(branch less than),bge(branch bigger than)을 잘안쓰는이유
  큰지 작은지 비교하는 것은 모든 비트를 살펴봐야해서, 같은지만 살펴보는 bne,beq보다 오래걸린다.
  따라서 bne,beq를 쓰는게 보통이다.