MAX HEAP

1.최대 힙(Max Heap)

먼저 완전이진트리(Complete Binary Tree)에 대해서 설명해야 한다.
완전 이진트리는 노드를 삽입할 때, 왼쪽부터 차례대로 삽입하는 트리이다.

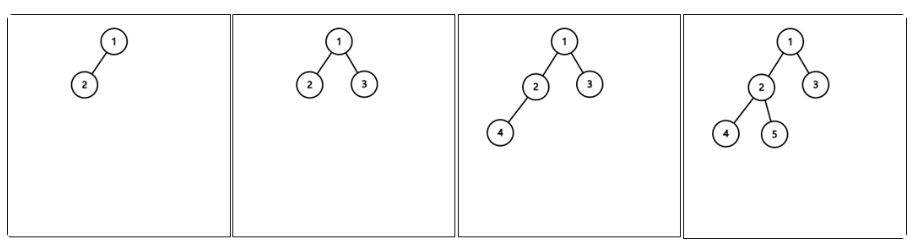
위와 같은 그림은 완전이진트리라고 할 수 있다.

그렇다면 밑에 그림은??

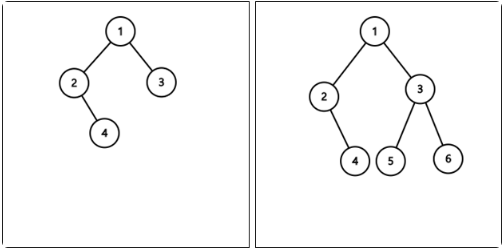
오른쪽부터 채워 졌으니 complete binary tree라고 볼 수 없다.

Max Heap 이란?

• Max Tree + complete binary tree 라고 볼 수 있다.
  Max Tree는 각 노드의 키 값이 자식의 키값보다 크거나 같은 트리이다.
  정리하면, 각노드의 값이 자식보다 크거나 같으면서 왼쪽부터 노드가 채워지는 Tree이다.

2. 최소힙(Min Heap)
   min heap은 max heap과 반대로 각 노드가 자식노드보다 작거나 같고 왼쪽부터 노드가 채워지는 Tree이다.
   min Tree + complete binary tree

3. Max Heap 에서의 삽입
   삽입은 무조건 마지막 노드에서 일어난다. 그이후 자신의 위치에 맞게 위로 올라간다.
   
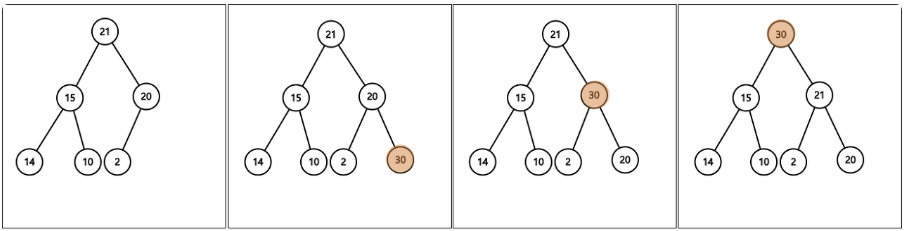
   30이 leaf 노드에 삽입되었다. 이후 30의 조상인 20과 비교한다.
   30이 더 크므로 위치를 바꿔준다.
   또 30이 조상인 21보다 크므로 위치를 한번더 바꿔준다.

참고로 삽입의 time complexity는 O(log(n))이다. 마지막에 삽입된 노드가 루트까지 거친다고 했을 경우 트리의 높이만큼 비교하기 때문이다.

4. Max Heap에서의 삭제
   삭제는 루트노드가 먼저 삭제된후 빈공간을 가장 마지막 노드와 자리를 바꿔준다. 이후에는 바뀌어진 루트의 값의 자리를 찾아주면 된다.
   

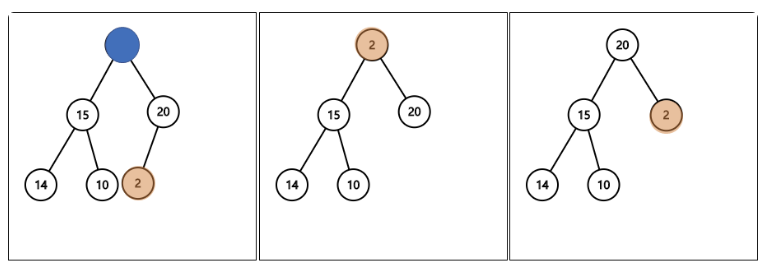
삽입의 time complexity도 마찬가지로 O(log(n))이다.

5.[Max Heap구현] //Min Heap은 부호만 반대로 해주면 된다.

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 1000

typedef struct _heap{
    int data[MAX_SIZE];
    int heap_index;
}heap;

heap* init(heap* h){
    h = (heap*)malloc(sizeof(heap));
    h->heap_index = 0;
    return h;
}
void add(heap* h, int data);
int delete(heap* h);
int empty(heap* h);

int main(){
    heap* h = NULL;
    h = init(h);
    add(h,3);
    add(h,5);
    add(h,1);
    add(h,23);
    add(h,9);

    printf("--------add-------\n");
    for(int i = 1; i<=h->heap_index; i++){
        printf("[%d]번 노드: %d\n",i+1,h->data[i]);
    }
    printf("------remove-------");
    
    //h의 index가 1이상이면 반복
    while(!empty(h)){
        printf("삭제한 값: %d\n",delete(h));
    }



}

int empty(heap* h){
    return (h->heap_index ? 0:1) ;
}

void add(heap* h, int data){
    //가장 마지막에 넣어준다.
    h->heap_index+=1;
    h->data[h->heap_index] = data;

    int me = h->heap_index;
    int parent = me / 2;
    //parent가 0보다 크면 반복, 계속 조상으로 가다보면 2로 나눠지는데,0이되면 조상이 없다는 뜻
    while(parent){
        //현재 값이 부모보다 크면 값을 바꿔준다.
        if(h->data[me] > h->data[parent]){
            int temp = h->data[me];
            h->data[me] = h->data[parent];
            h->data[parent] = temp;
            //내위치를 부모로 바꿔준다.
            me = parent;
            parent = me /2;
            }

        else{
            break;
        }
    }
    return;
}

int delete(heap* h){
    //가장 큰값을 res에 저장
    int res = h->data[1];
    //가장 마지막 노드의 값을 루트노드와 교체 하고 크기를 하나 줄인다.
    h->data[1] = h->data[h->heap_index];
    h->heap_index -=1;

    int me = 1;
    int child = 2;
    //자식노드 인덱스가 힙 인덱스 사이즈 보다 작으면 반복
    while(child <=h->heap_index){
        //비교할 왼쪽 자식노드보다 오른쪽자식노드가 크면 인덱스를 오른쪽으로 넘긴다.
        if(h->data[child] < h->data[child+1] && child+1 <= h->heap_index ){
            child++;
        }
        //현재 노드보다 자식 노드가 크다면 바꿔준다.
        if(h->data[me] < h->data[child]){
            int temp;
            temp = h->data[me];
            h->data[me] = h->data[child];
            h->data[child] = temp;
            //내 위치를 바꾼 인덱스 위치로
            me = child;
            child = me*2;
        }

        //내가 더크면 제자리 이므로 종료
        else{
            break;
        }
    }
    //처음에 삭제했던 루트 값 반환
    return res;
}

[출처]:https://juhee-maeng.tistory.com/94
[출처]:https://seongjuk.tistory.com/entry/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%9E%99-Heap-CC-%EA%B5%AC%ED%98%84-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%B5%9C%EC%86%8C-%ED%9E%99-%EC%B5%9C%EB%8C%80-%ED%9E%99