[알고리즘] 하노이 퍼즐

하노이 퍼즐

n개의 각각 다른 사이즈를 갖는 디스크를 첫번째 원통에 넣었다.

목표는 첫번째 원통을 세번째 원통으로 옮기는 것이다.

n > 1 클때, n개의 디스크를 옮길때 제약은 다음과 같다.

• 한번에 한개의 디스크만 옮길 수 있다.
• 작은것보다 큰것이 위에 있는것은 안된다.
• 가운데 원통을 보조로 사용할 수 있다.

출처: https://shoark7.github.io/programming/algorithm/tower-of-hanoi
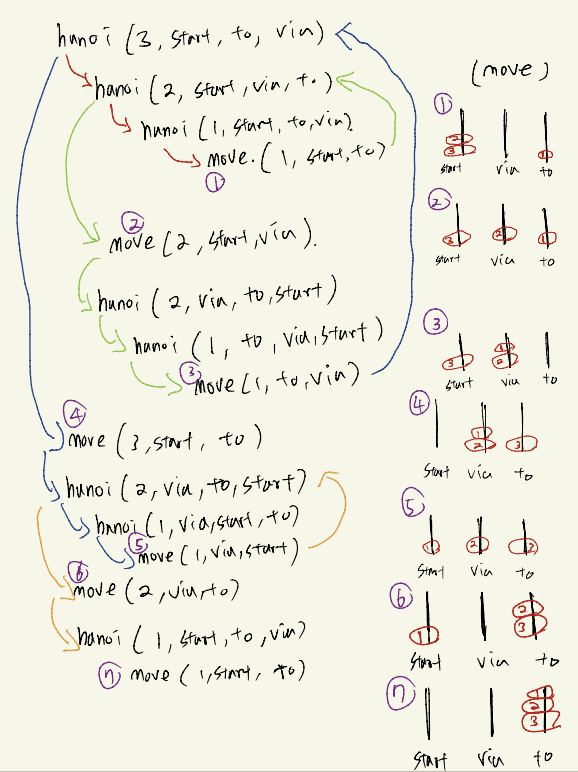
hanoi(n,start,to,via)는 n개의 디스크를 start에서 to로 via를 경유해서 옮기겠다는 함수이다.

move(n,start,to)는 n번째 디스크를 start에서 to로 이동시킨다는 함수이다.

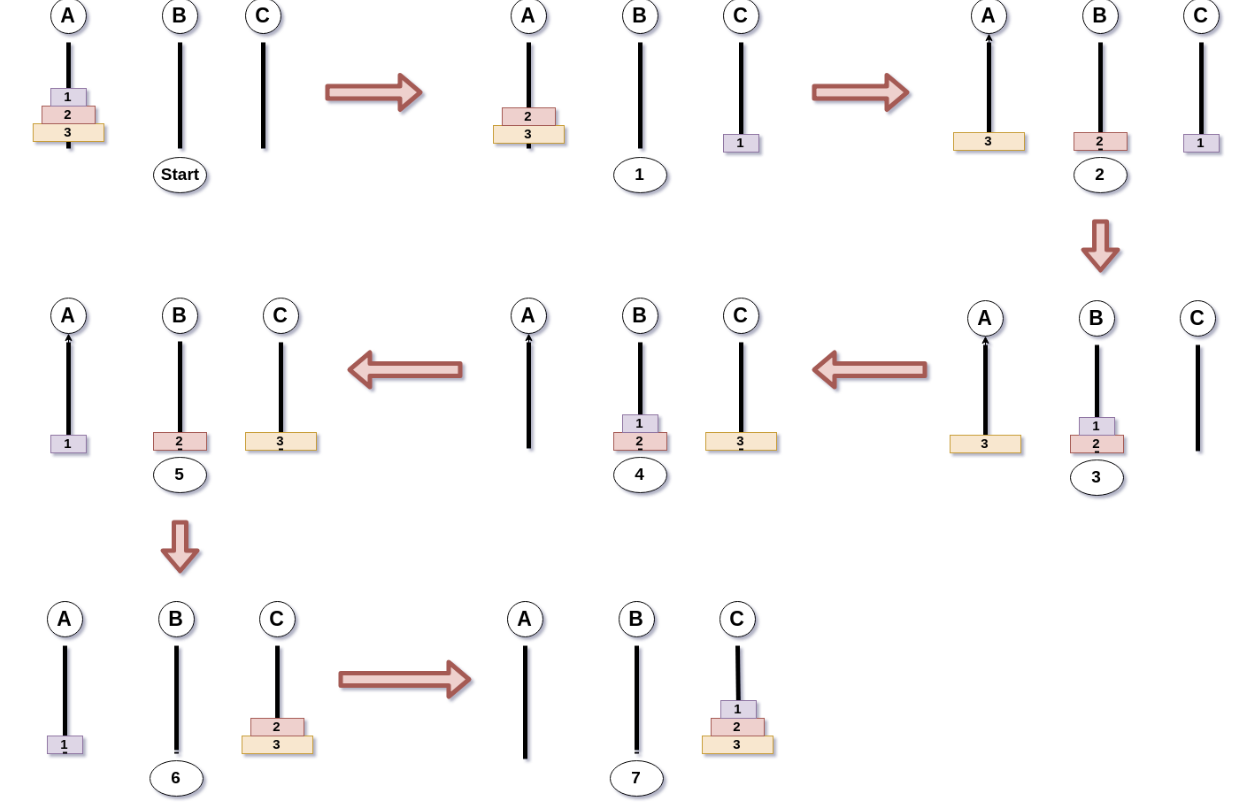
A는 start(시작) B는 via(경유지) C는 to(목표)이다

위 그림을 토대로 설명하면,

1. hanoi(3,A,C,B)

   3개의 디스크를 A에서 시작하여 B를 경유해서 C로 옮기겠다.

2. hanoi(2,A,B,C)

   3번 디스크를 옮기기 위해서는 반드시 1,2번 디스크가 경유지에 있어야 한다.
   C에는 3번 디스크가 들어가야 하기때문에 2번 디스크의 목표가 C가 될 수 없다. 따라서, A에서 시작해서 C를 경유해서 B를 목표로한다.

3. hanoi(1,A,C,B),move(1,A,C)

   2번 디스크의 목표가 B이므로 1번 디스크는 목표가 C가 되어야 한다. 따라서 A에서 시작해서 B를 경유해 C를 목표로 하고 이동한다.

4. move(2,A,B)

   2번 디스크를 목표(B)로 이동시킨다.

5. hanoi(1,C,B,A),move(1,C,B)

   1번디스크를 2번위에 올려야 하기 때문에 2번 디스크의 목표인 B로 이동한다.

6. move(3,A,C)

   3번 디스크를 목표인 C로 이동시킨다.

7. hanoi(2,B,C,A)

   2번디스크가 3번디스크 위로 올라갈 수있도록 목표를 C로 한다.

8. hanoi(1,B,A,C),move(1,B,A)

   1번 디스크는 현재 B에 위치해 있고 2번디스크의 목표가 C 이므로 목표를 A로 하고 이동한다.

9. move(2,B,C)

   2번 디스크를 C로 이동시킨다.

10. hanoi(1,A,C,B),move(1,A,C)

    1번 디스크를 C로 이동시킨다.

엄청 복잡한것 같지만 사실은 단순한 과정이다.
1. 가장 아래 있는 n번째 디스크를 목표로 이동시켜야 한다.
2. n번째를 목표로 이동시키기 위해서는 그위에 n-1 번째까지의 디스크들이 via로 이동해야한다.
3. n번째 디스크가 목표로 이동하고 난후 n-1번째 까지의 디스크를 목표로 n번째 디스크위인 목표로 이동해준다.

이것을 재귀함수로 나타내면 다음과 같다.

int hanoi(n,start,to,via){
	if(n == 1){
    	move(1,start,to);
        return;
    }
    else{
    	hanoi(n-1,start,via,to);
        move(n,start,to);
       hanoi(n-1,via,to,start);
    }
}

그림으로 그리면...

time complexity

위의 함수들을 이동수를 따진다면,
M(n)=M(n-1)+1+M(n-1) = 2M(n-1)+1
M(1)=1
으로 볼 수 있다.

이것을 통해 time complexity를 backward substitions method로 알아낼 수 있다.

$M(n) = 2M(n-1)+1$
$M(n) = 2M(2M(n-2)+1)+1 = 2^2M(n-2)+2+1$
$M(n) = 2^2M(2M(n-2)+1)+2+1 = 2^3M(n-3)+2^2+2+1$

i번째 후..

$M(n) = 2^iM(n-i)+2^{i-1}+2^{i-2}+...+2+1$

이걸 정리하기 위해서는

등비수열의 합을 이용해야 한다.

$\frac{a(2^n-1)}{r-1}$

이식에 의해서

$M(n) = 2^iM(n-i)+2^i-1$

i=n-1 일때,

$M(n) = 2^{n-1}M(n-(n-1))+2^{n-1}-1$
$M(n) = 2^{n-1}M(1)+2^{n-1}-1$
$M(n) = 2^{n-1}+2^{n-1}-1$
$M(n) = 2(2^{(n-1)})-1$
$M(n) = 2^{n}-1$

따라서 time complexity는 $O(2^n)$ 이다.