크루스칼 알고리즘은 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘이다.
즉, 최소 비용 신장 트리를 만들기 위한 알고리즘 이라고 할 수 있다.
실제로, 여러개의 도시(노드)가 있을때 가장 적은 비용으로 도로를 연결하고자 할때 적용하는 알고리즘이다.
노드 = 정점 = 도시
간선 = 거리 = 비용
다음은 노드 7개 간선 11개인 그래프이다.
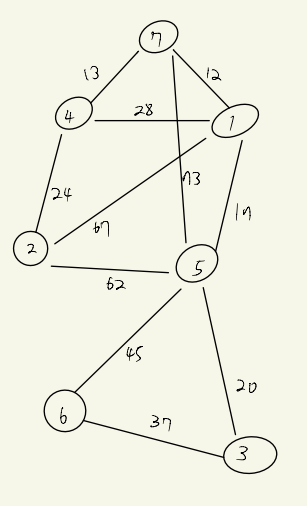
앞에서 설명했던 것처럼 모든 노드를 연결하면서 비용이 가장 적어야 하고,반드시 간선의 수는 노드갯수-1 이어야 한다.
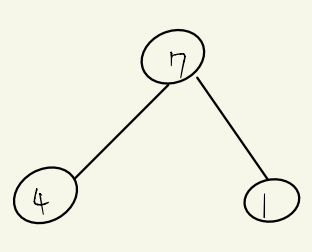
먼저 사이클을 설명하자면
사이클이 형성되지 않은경우
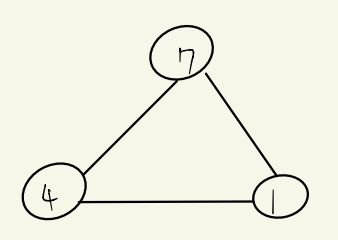
사이클이 형성된 경우
알고리즘은 다음과 같다.
1. 비용이 가장 적은 간선부터 하나씩 연결한다.
2. 연결하다가 사이클이 발생하면 건너뛴다.
예를들면 밑의 순서로 간선을 연결한다.
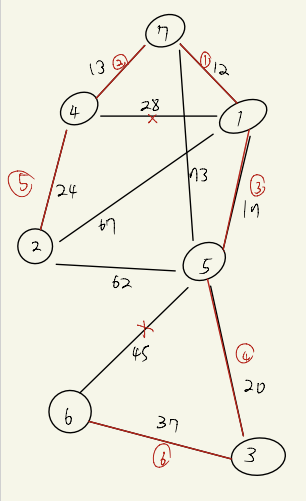
이렇게 연결하면 간선 = 노드-1이 충족된다.
28과 45에 x 표가 쳐져 있는 이유는 사이클이 형성되기 때문이다.
데이터는 어떤식으로 형성이 되어 있느냐
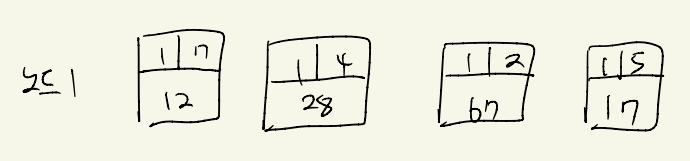
노드 1에는 7,4,2,5 노드가 연결되어 있다.
1,7노드를 연결하는 간선의 비용은 12이고
1,4는 28
이런식으로 데이터 값을 준다.
이러한 모든 데이터를 간선의 비용 순서대로 나열한다.
그러고 나서 사이클 테이블을 만들어 주는데 합집합 알고리즘에서 만들었던 union-find를 사용할 것이다.
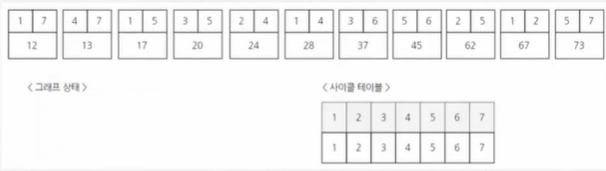
사이클 테이블의 윗줄은 자신의 노드 아랫줄은 부모노드 이다.
하나씩 시작해보면
- 가장 작은 간선인 7과 1을 연결했다. 그러면 더 큰 수의 노드인 7이 1을 parent로 한다.
그러면 다음과 같이 사이클 테이블이 만들어진다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 1 |
- 다음으로 작은 간선 4와 7을 연결했다. 4는 7의 부모가 1이므로 1을 가리키게 된다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 5 | 6 | 1 |
- 1과 5를 연결했다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 1 | 6 | 1 |
- 3과 5를 연결했다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 1 | 6 | 1 |
- 2와 4를 연결했다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 6 | 1 |
- 1과 4를 연결하려고 봤더니 부모가 같다. 따라서 cycle이 발생하게 되어 무시하고 넘어간다.
7.3과 6을 연결하였다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
총 비용은 연결된 값들의 비용을 모두 더한다.
즉, 12+13+17+20+24+37 = 123 이다.
구현은 어떻게 해야하는지 알아보자
C++ 구현
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//부모노드를 찾는 함수
int getParent(int parent[],int a){
if(parent[a] == a) return a;
return parent[a] = getParent(parent,parent[a]);
}
//각 노드의 부모를 합치는 함수
void unionParent(int parent[],int a,int b){
a = getParent(parent,a);
b = getParent(parent,b);
if(a < b) parent[b] = a;
else parent[a] = b;
}
//각 노드가 같은 그래프에 속해있는지 확인하는 함수
int findParent(int parent[], int a,int b){
a = getParent(parent,a);
b = getParent(parent,b);
if(a == b) return 1;
return 0;
}
class Edge{
public:
int node[2];
int distance;
Edge(int a,int b, int distance){
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
bool operator<(Edge &edge){
return this->distance < edge.distance;
}
};
int main()
{
int n = 7; //노드 개수
int m = 11; //간선 개수
vector<Edge> v;
v.push_back(Edge(1,7,12));
v.push_back(Edge(1,4,28));
v.push_back(Edge(1,2,67));
v.push_back(Edge(1,5,17));
v.push_back(Edge(4,7,13));
v.push_back(Edge(2,4,24));
v.push_back(Edge(2,5,62));
v.push_back(Edge(5,6,45));
v.push_back(Edge(5,7,73));
v.push_back(Edge(3,5,20));
v.push_back(Edge(3,6,37));
//간선의 비용 순서대로 정렬
sort(v.begin(),v.end());
//각정점이 포함된 그래프가 어디인지 저장
//cycle table
int parent[n];
for(int i=0; i<n; i++){
parent[i] = i;
}
int sum = 0;
for(int i = 0; i < v.size(); i++){
//사이클이 발생하지 않는 경우 그래프에 포함
//parent의 인덱스가 7이므로 v[i].node -1(parent의 index번호)을 해줘야함.
if(!findParent(parent,v[i].node[0]-1,v[i].node[1]-1)){
sum += v[i].distance;
unionParent(parent,v[i].node[0]-1,v[i].node[1]-1);
}
}
printf("%d\n",sum);
return 0;
}결과값:123
java 구현
import java.util.*;
class Edge{
int a;
int b;
int edge;
public Edge(int a,int b,int edge){
this.a = a;
this.b = b;
this.edge = edge;
}
}
class Main{
public static void main(String[] args) {
int totalEdge = 0; //간선의 총합
//그래프 초기화
Vector<Edge> graph = new Vector<>();
graph.add(new Edge(1,7,12));
graph.add(new Edge(1,4,28));
graph.add(new Edge(1,2,67));
graph.add(new Edge(1,5,17));
graph.add(new Edge(4,7,13));
graph.add(new Edge(2,4,24));
graph.add(new Edge(2,5,62));
graph.add(new Edge(5,6,45));
graph.add(new Edge(5,7,73));
graph.add(new Edge(3,5,20));
graph.add(new Edge(3,6,37));
//edge 크기 순으로 정렬
Collections.sort(graph, new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.edge - o2.edge;
}
});
//cycle table 초기화
int[] parent = new int[7];
for(int i=0; i<parent.length; i++){
parent[i] = i;
}
for(Edge a:graph){
if(getParent(parent,a.a-1) != getParent(parent,a.b-1)){
unionParent(parent,a.a-1,a.b-1);
totalEdge += a.edge;
}
}
System.out.println(totalEdge);
}
static public int getParent(int[] parent, int a){
if(parent[a] == a) return a;
else return parent[a] = getParent(parent,parent[a]);
}
static public void unionParent(int[] parent, int a, int b){
a = getParent(parent,a);
b = getParent(parent,b);
if(a<b) parent[b] = a;
else parent[a] = b;
}
static public Integer[] putEdge(int a,int b, int edge){
Integer[] graph = new Integer[3];
graph[0] = a;
graph[1] = b;
graph[2] = edge;
return graph;
}
}
