1. Verifying Functional Programs
Functional programming in Isabelle/HOL can be performed directly, as Isabelle supports functional programming. Verification typically involves stating and proving properties about functions. For instance, if we have a recursive function to calculate the factorial of a number:
fun factorial :: "nat ⇒ nat" where
"factorial 0 = 1" |
"factorial (Suc n) = Suc n * factorial n"A property to verify could be that the factorial of any natural number is not zero:
theorem factorial_not_zero:
"factorial n ≠ 0"We could then prove this theorem in Isabelle.
2. Imperative Programming(Circus)
There's a framework called Isabelle/IMP that you can use to reason about imperative programs. This framework allows you to define programs in an imperative language, along with a semantics, and reason about these programs using Hoare logic.
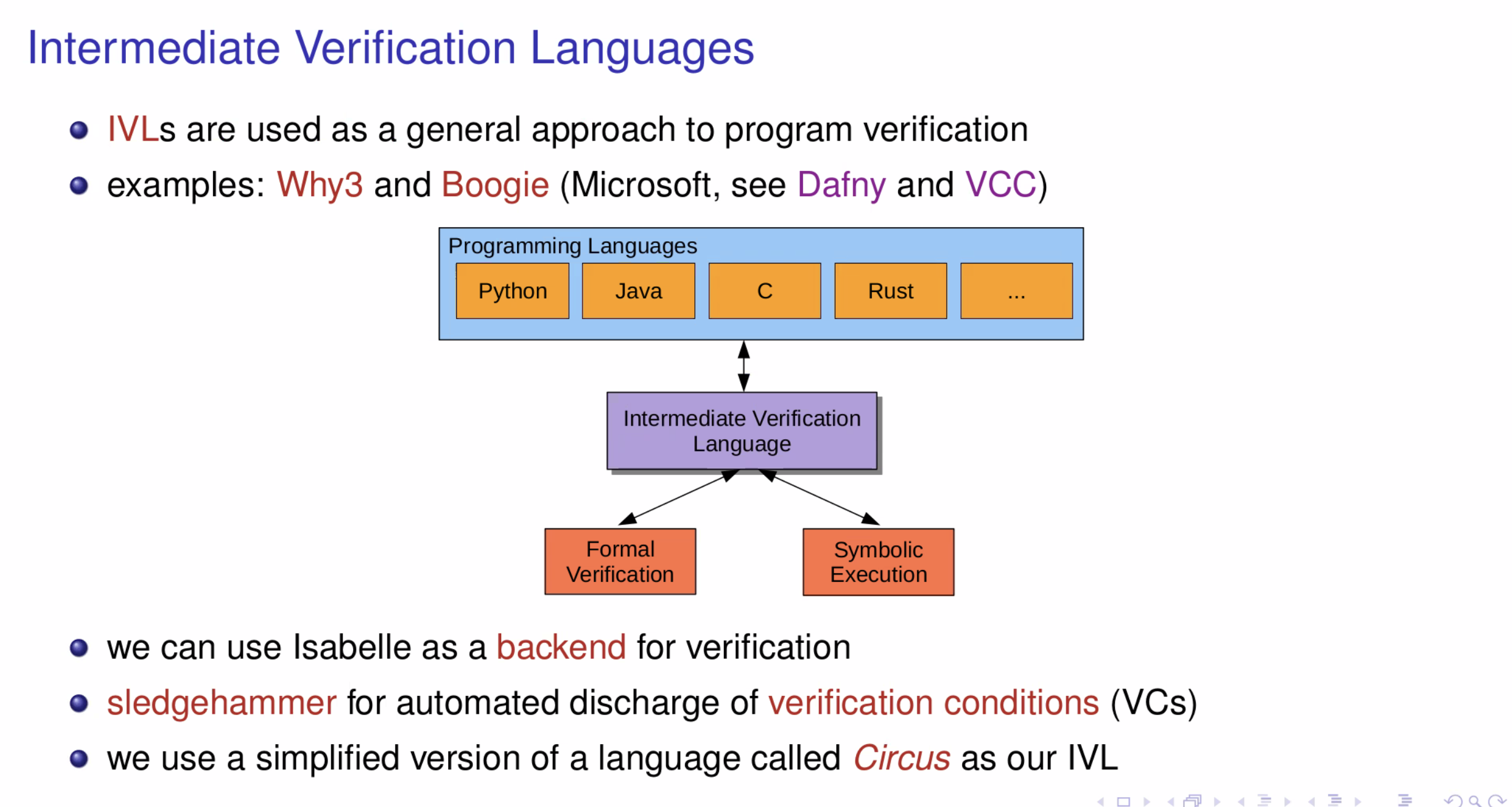



3. Hoare Logic
Hoare logic is a way to reason about imperative programs. In Isabelle/HOL, you can use the Isabelle/IMP framework to define Hoare triples {P} c {Q}, where P and Q are predicates describing pre- and post-conditions of the command c.
For example, given a command x := x + 1, you could specify a Hoare triple like {x = n} x := x + 1 {x = n + 1}, which asserts that if x equals n before the command is executed, x will equal n + 1 after execution.
4. Loop Invariants
Loop invariants are a concept from Hoare logic and are conditions that hold before and after each iteration of a loop. They're crucial when reasoning about loops in Hoare logic.
For instance, consider a while loop in the Isabelle/IMP language: WHILE b DO c. A loop invariant P would be a predicate such that {P ∧ b} c {P} holds - i.e., if P is true and the loop's condition b is true before executing the loop body c, then P will still be true afterward.
Proving that such an invariant holds and that it implies the desired post-condition can be used to prove properties of the loop in the Hoare logic framework.