논문 제목: On Decomposing a Deep Neural Network into Modules
📕 Summary
Abstract
- The paper proposes decomposing a deep neural network (DNN) into modules to bring the benefits of modularity to deep learning.
- The authors develop a methodology for decomposing DNNs for multi-class problems and demonstrate that this decomposition enables reuse of DNN modules and replacement of modules without retraining.
Introduction
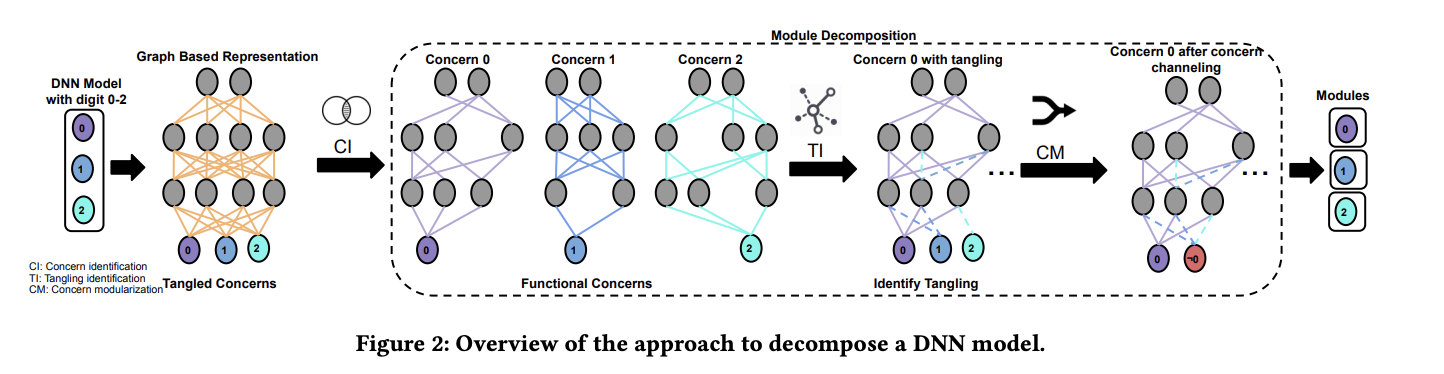
- The paper discusses the incorporation of deep learning in modern software systems and the need for modularity in deep neural networks (DNNs) to enable easier logic changes and flexibility in the models.
- It introduces the concept of decomposing a DNN into modules, similar to decomposing software code, to bring the benefits of modularity to deep learning.
- The authors argue that by decomposing a DNN into modules, it becomes possible to reuse and replace modules without the need for retraining the entire network.
- The paper presents a methodology for decomposing DNNs for multi-class problems and demonstrates its effectiveness on four canonical datasets.
- The goal is to create DNN models that are at least as good as traditional monolithic DNNs in terms of test accuracy, while enabling easier modification and reuse of modules.
📕 Solution
Algorithm 1 Concern Identification (CI)

- CI is a procedure that takes five inputs: a model, an input, an indicator, D, and b.
- The input is denoted as X, and the weight and bias of the model are extracted using the extractWB function, which returns W and B.
- The algorithm then computes the value of the nodes in each layer of the model using a for loop that iterates over each layer.
- If the indicator is set to True, the algorithm does not change the value of the edges in the model.
- If the indicator is set to False, the algorithm updates the value of the edges in the model based on the values of the nodes in the previous layer.
- The algorithm then returns the updated value of the edges in the model as D.
Algorithm 2 Tangling Identification (TI)

- Algorithm 2, which is called Tangling Identification (TI).
- TI is a procedure that takes as input a deep neural network (DNN) model, an input, an indicator, a matrix D, and a bias vector b.
- The input X is initialized with the given input, and the weights and biases of the DNN model are extracted and stored in matrices W and B, respectively.
- The algorithm then computes the value of the nodes in each layer of the DNN model using the input X and the extracted weights and biases.
- The output of the last layer is then passed through a softmax function to obtain the predicted class probabilities.
- The negative edges of the DNN model are updated by setting the corresponding entries in the matrix D to the corresponding entries in the weight matrix W if the value of the node is positive, and leaving them unchanged otherwise.
- The output layer edges are updated by setting the corresponding entries in the matrix D to the corresponding entries in the weight matrix WL if the predicted class probability is greater than a threshold value, and setting the corresponding entries in the bias vector bL to the corresponding entries in the bias vector BL.
- The updated matrix D is returned as the output of the procedure.
Algorithm 3 Tangling Identification: Imbalance (TI-I)

- Algorithm 3, which is called Tangling Identification: Imbalance (TI-I).
- TI-I is a procedure that takes as input a deep neural network (DNN) model, training data (Xtrain and Ytrain), a positive class (class), and a negative class (negativeclass).
- The procedure first extracts the weight and bias parameters of the DNN model using the extractWB function.
- It then initializes two matrices D and b with the extracted weight and bias parameters, respectively, and sets an indicator variable to False.
- The procedure then filters the positive examples from the training data and updates the positive edges of the DNN model using the CI function for the first 1000 positive examples.
- If the number of non-zero elements in the updated weight matrix DL is less than or equal to 10% of the total number of elements in DL, the indicator variable is set to False to stop further updates.
- The procedure then updates the negative edges of the DNN model for each example in the negative class using the TI function.
- The negative examples are filtered from the training data, and for each example, the TI function updates the weight and bias matrices D and b, respectively.
Finally, the procedure returns the updated weight and bias matrices D and b.
Algorithm 4 Concern Modularization: Channeling (CM-C).

- Algorithm 4, which is called Concern Modularization: Channeling (CM-C).
- This algorithm is a procedure that takes three inputs: D, b, and class.
- The algorithm uses a for loop to iterate over the rows of D, which is a matrix representing the weights of a deep neural network (DNN).
- If the class input is 0, then the algorithm assigns the second node as the negative node.
- The algorithm then computes the mean of the first column of the current row and assigns it to the first element of the row.
- The algorithm sets all the values in the second column of the row to 0.
- The algorithm computes the mean of the first row of D and assigns it to the first element of the first row of D.
- The algorithm sets all the values in the second row of D to 0.
- If the class input is not 0, then the algorithm assigns the first node as the negative node.
- The algorithm initializes two empty lists, tempW and tempB, and a counter variable k to 0.
- The algorithm uses another for loop to iterate over the elements of b, which is a vector representing the biases of the DNN.
- If the current element is not equal to the class input, then the algorithm appends the corresponding element of the current row of D to tempW and the current element of b to tempB.
- The algorithm computes the mean of tempW and assigns it to the first element of the current row of D.
- The algorithm computes the mean of the first row of D and assigns it to the first element of the first row of D.
- The algorithm sets all the values in the third row of D to 0.
- The algorithm updates the current row of D with the values in temp.
- Finally, the algorithm returns the updated D and b.
Algorithm 5 Concern Modeularization: Remove Irrelevant Edges (CM-RIE).

- Algorithm 5, which is a procedure for modularizing a deep neural network (DNN) by removing irrelevant edges.
The procedure takes as input the DNN (represented as a matrix D), a bias vector b, and a class label. - The procedure first initializes two empty lists, temp1 and temp2, and a temporary count variable, tempCount.
- It then iterates over each row i in the DNN matrix D, and checks if the value of DL[i, class] is zero, indicating that the row corresponds to an irrelevant node for the given class.
- If the row corresponds to an irrelevant node, the procedure iterates over each column j in the DNN matrix D, except for the column corresponding to the given class.
- If the value of DL[i, j] is non-zero, indicating that there is an edge between nodes i and j, the procedure adds the weight of the edge to the list temp1 and the index j to the list temp2.
- The procedure then computes the mean of the negative edges for the irrelevant nodes, and updates the DNN matrix D accordingly.
- If there is more than one irrelevant node, the procedure merges the edges by computing the mean of the weights and updating the DNN matrix D accordingly.
- Finally, the procedure compensates for the flow by updating the DNN matrix D-1, applies the concern channeling approach, and returns the updated DNN matrix D and bias vector b.
📕 Conclusion
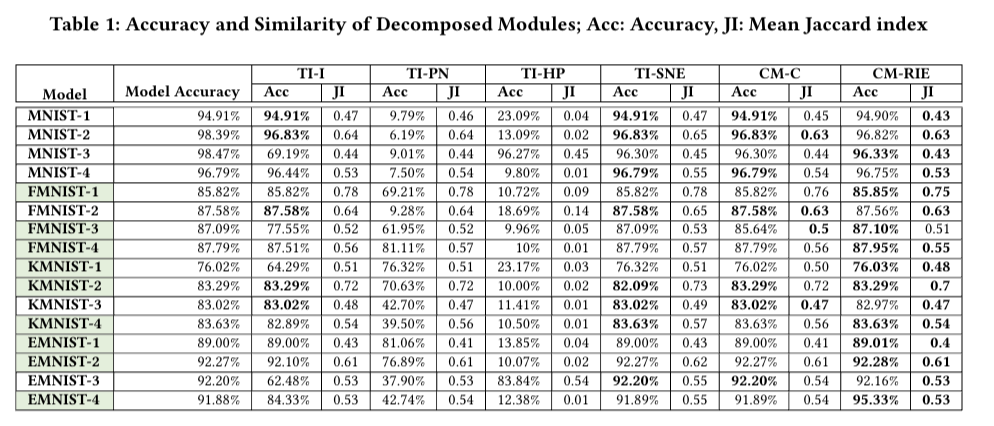
- The paper demonstrates that decomposing a deep neural network (DNN) into modules enables the reuse and replacement of DNN modules without the need for retraining. This is achieved by developing a methodology for decomposing DNNs for multi-class problems. The authors evaluate their approach using four canonical datasets and sixteen different models, and find that the decomposed modules are slightly more accurate or lose very little accuracy compared to traditional monolithic DNNs.
- The benefits of decomposing a DNN into modules are observed in enabling modularity and flexibility in deep learning systems. The authors believe that this work takes the first step toward enabling more modular designs for deep learning and suggest future avenues for improving the accuracy of DNN modules, exploring decomposition for other types of DNNs, and exploring unit-testing and composition of DNN modules with traditional functions
Contribution
- The paper introduces a methodology for decomposing deep neural networks (DNNs) into modules, similar to decomposing monolithic software code into modules, to bring the benefits of modularity to deep learning.
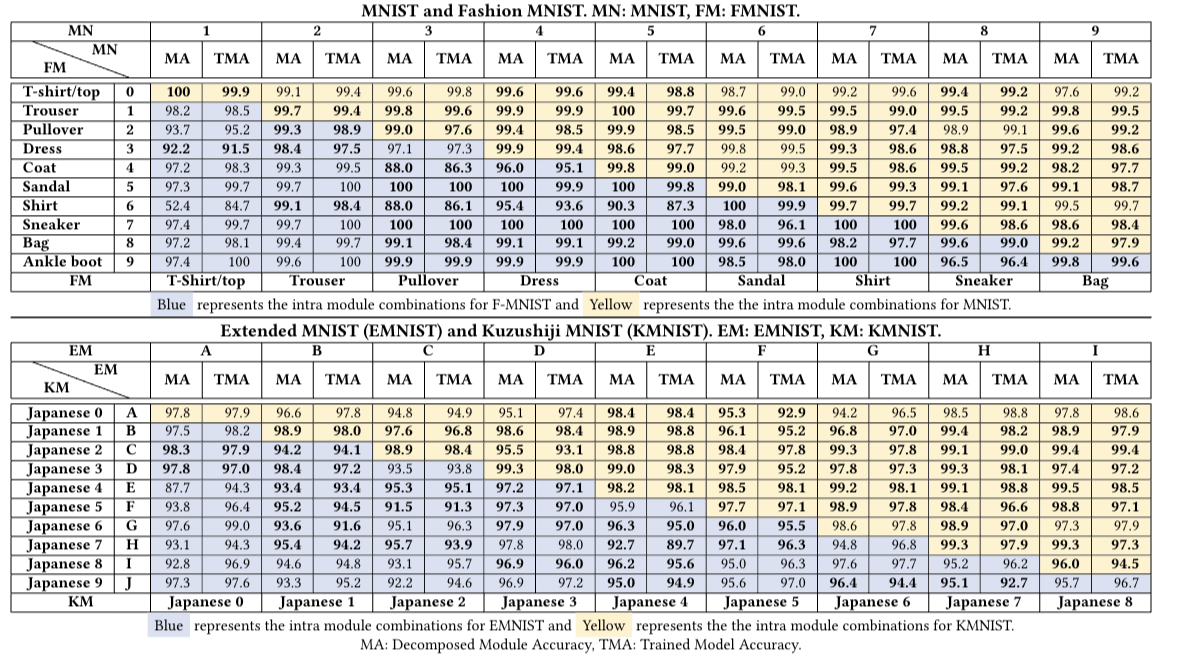
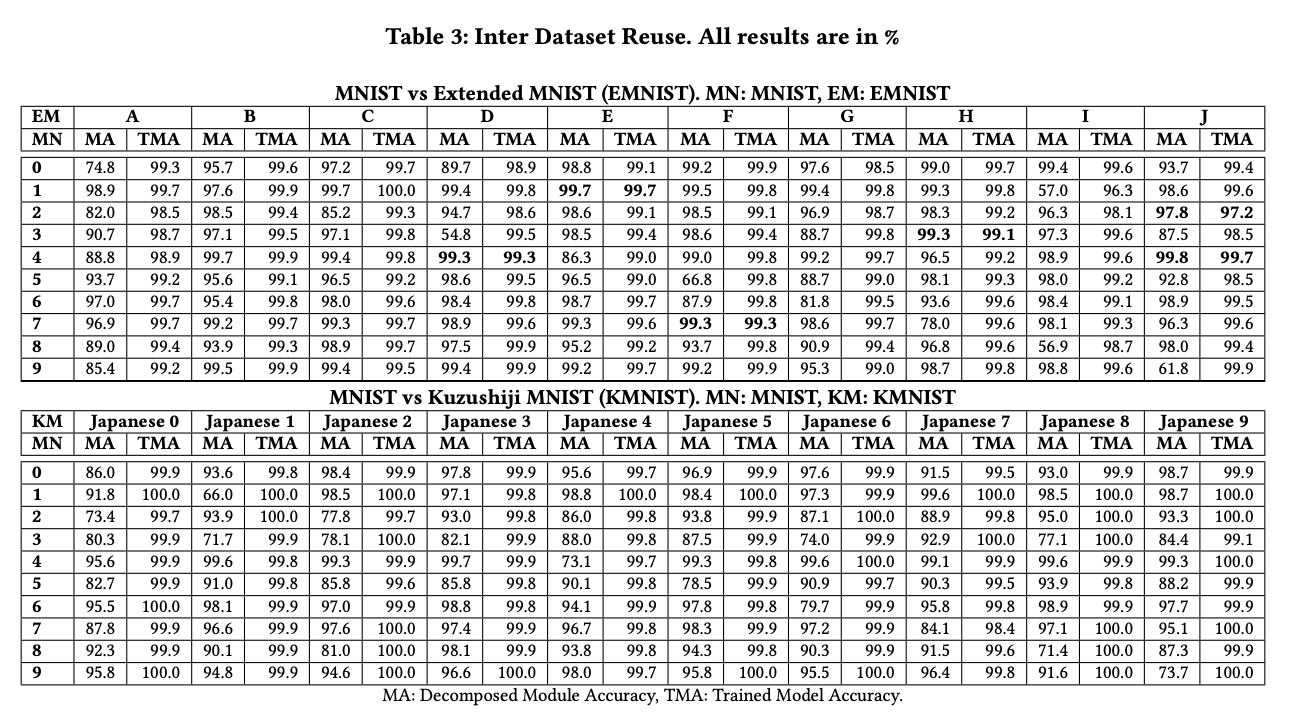
- The authors demonstrate the feasibility of decomposing DNNs for multi-class problems by applying their methodology to four canonical datasets (MNIST, EMNIST, FMNIST, and KMNIST). They show that the decomposed DNN modules can be reused and replaced without the need for retraining, while still achieving comparable test accuracy to traditional monolithic DNNs.
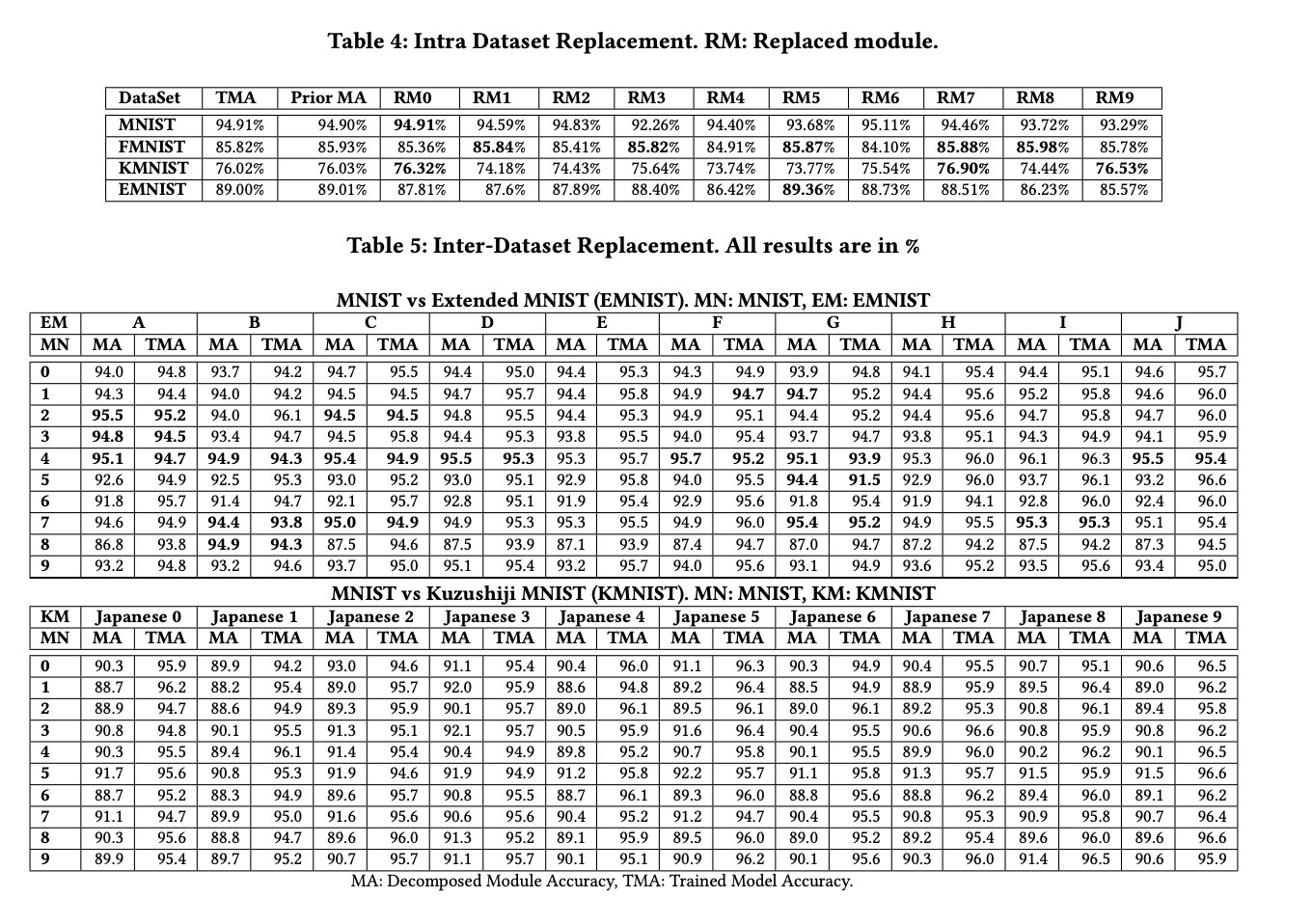
- The work highlights the potential of decomposed DNN modules in enabling modularity and flexibility in deep learning systems, allowing for easier logic changes and the creation of different DNNs by reusing modules.
- The authors suggest future directions for improving the accuracy of DNN modules, exploring decomposition for other types of DNNs, and investigating unit-testing and composition of DNN modules with traditional functions