Graph Convolutional Networks (GCN)

본 글은 Semi-Supervised Classification with Graph Convolutional Network 논문을 바탕으로 설명하는 글입니다.

왜 이 논문인가?

Graph Neural Networks의 장점은 앞선 글에서 설명한 바 있다. 우리가 다루는 많은 정보는 graph의 형태로 이해할 수 있는데, 이 구조를 기존의 convolution 또는 recurrent model로는 제대로 다루기 어렵다. 그 이유는 크게 세가지가 있다.

1. 격자(grid) 구조로 그래프를 다룰 수 없다. 그래프란 이미지나 다른 데이터와는 달리 그 구조적인 형태가 매우 자유롭다
2. 서로 다른 두 node의 관계를 보다 풍부하게 표현할 필요가 있다.
3. 그래프 내에는 여러 가지 성질을 가진 entity가 있어 이들을 동등하게 고려하는 것은 불공평하다.

때문에 우리는 그래프를 그래프답게 다뤄야 하는데, 본 논문이 그 중 굉장히 유명하다. 그 이유는 convolution의 개념을 그래프에 도입하여 우수한 성능을 보여줬기 때문이다.

이 논문의 목적

Node-level Semi-supervised Learning
우리가 가지고 있는 그래프에는 모든 node가 레이블링 되어 있지는 않다 (몇개는 되어있고, 몇개는 안되어있다). 그렇다면 우리가 알고 있는 node를 활용하여 정체를 모르는 node들을 맞출 수 있을까??

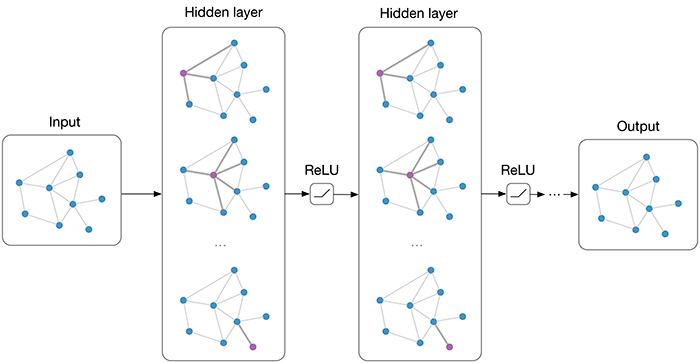
Graph Convolutional Network
기존 많은 딥러닝 연구에서 큰 성공을 거둔 convolution-based 방법을 그래프에도 도입시킬 수 있지 않을까??
(결과적으로 First-order approximation of spectral graph convolution이라는 방법으로 graph에 convolution을 성공적으로 도입)

그래프에 Convolution이 왜 필요한데? 무슨 의미인데?

신호처리 문제에서 convolution은 두 신호 $f$와 $g$에 대해 $f\ast g$로 표현하며, 이것은 $f$가 $g$에 의해 어떻게 변형되는가를 나타낸다. 두 신호의 integral로 해석할 수도 있기 때문에 만약 어떤 지점에서 결과값이 크다면 해당 지점에서의 두 신호는 서로 큰 양의 상관관계를 갖는다. (정확히는 $f$ 또는 $g$ 한쪽은 inverse되어 계산되지만...)
아무튼 두 데이터 간의 상관관계를 파악하는데 참 좋은 방법이 convolution이다.

그래프에 convolution을 적용한다는 말은, 그게 가능하다면 임의의 두 node 사이의 관계의 정도를 파악하는데 매우 효과적일 것이다.
정리하자면 그래프 내의 임의의 node 사이의 관계를 추론함으로써, 정체를 알고 있는 node를 활용하여 정체를 모르는 node들을 알아내는 것이 이 논문의 목적이다. 기존에 graph Laplacian을 활용한 graph smoothing을 했던 연구가 있었다.

이제 이해했으니 그래프 Node간의 관계를 파악하기 위한 convolution을 해보자

이 블로그에 너무도 자세히 설명되어 있으니 참고하자.

$H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})$

이 논문에서 Multi-layer GCN을 제안하였고 수식은 위와 같다. 차근차근 이해해보자. 그래프에서의 spectral convolution은 Fourier domain에서의 아래와 같은 연산으로 정의할 수 있다.

$g_{\theta}\star x = Ug_{\theta}U^{T}x$

$x\in \mathbb{R}^{N}$: 각 node의 scalar representation (vector인 경우는?)
$U$: normalized graph Laplacian $L = I_{N}-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U\Lambda U^{T}$의 eigenvector로 이루어진 matrix
$g_{\theta}$: $\theta$의 diagonal matrix ($diag(\theta)$). $\theta \in \mathbb{R}^{N}$

식을 가만 보면 $g_{\theta}$를 $L$의 eigenvalues ($\Lambda$)로 이루어진 함수 $g_{\theta}(\Lambda)$라고 이해할 수 있다.

이 연산을 하기 위해서는 $O(N^2)$의 complexity를 갖는 것을 알 수 있다. 이게 의미하는 것은 만약 우리의 그래프가 백만개, 천만개, 일억개가 넘는 node를 갖고 있다면 과연 이 계산을 쉽게 할 수 있을까? 아마 멈춰버린 컴퓨터를 하루종일 바라봐야 할 지 모른다.
하지만 Hammond et al. 논문에서 $g_{\theta}(\Lambda)$를 Chebyshev polynomials $T_{k}(x)$로 근사할 수 있다고 소개한 바 있다. 따라서 위의 $g_{\theta}(\Lambda)$는

$g_{\theta'}(\Lambda) \approx \sum_{k=0}^{K}\theta_{k}'T_{k}(\tilde{A})$

$\tilde{\Lambda} = \frac{2}{\lambda_{max}}\Lambda-I_{N}$: 기존 eigenvalues의 집합을 rescale 한 것.
$\theta'\in \mathbb{R}^{K}$: Chebyshev coefficients

그래서 결론은 우리의 목표 $g_{\theta'} \star x$는 아래와 같이 근사할 수 있다는게 결론이다.

$g_{\theta'} \star x \approx \sum_{k=0}^{K}\theta_{k}'T_{k}(\tilde{L})x$

이 결론이 주는 중요한 포인트는

1. Convolution의 근사: Chebyshev polynomials을 통해 그래프의 spectral convolution을 polynomial의 형태로 근사시켰다.
2. K값이 갖는 의미: 논문에서 K-localized라고 표현했으며, 이는 기준 node에서 몇 hop의 neighborhood까지 계산할 것인가를 말해준다.
3. Complexity: 기존 $O(N^2)$에서 $O(|E|)$로 줄었다. (정확히는 Complete graph에서 $|E|$는 $O(N^2)$이며, 이 경우가 upper bound인 셈)