앞선 글들에서 GNNs의 소개를 했다. 그러면 구체적으로 어떤 종류의 모델이 있고 어떤 특징이 있는지 살펴보자.
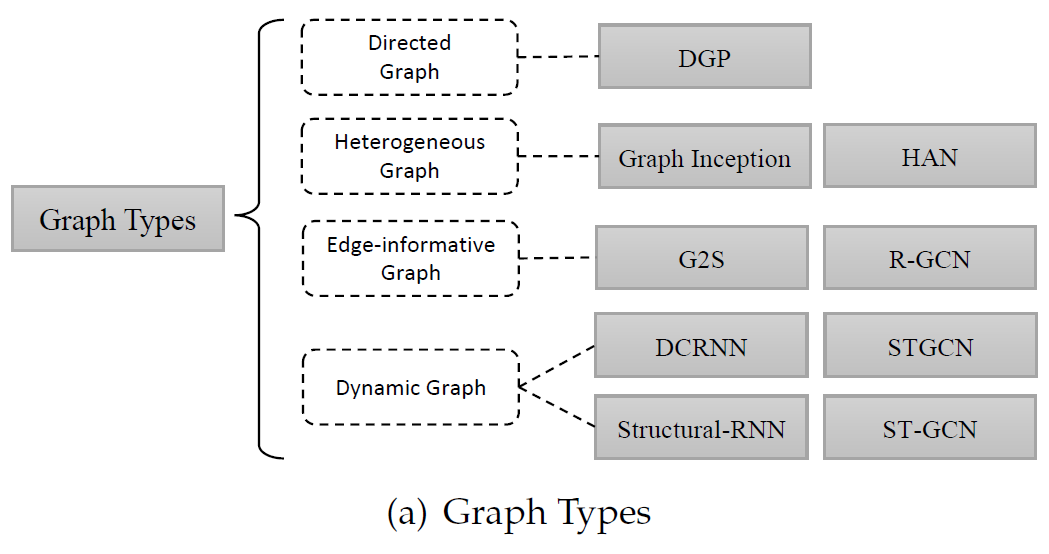
Graph Types에 대한 연구
Directed Graph
그래프 수업을 들으면 가장 처음에 들을 수 있는 개념이다. 두 노드 사이의 방향이 존재하는 그래프. 보통 백화점을 가면 directed escalator(에스컬레이터)를 볼 수 있다.
Homogeneous / Heterogeneous Graph
Homogeneous graph는 그래프의 모든 노드가 같은 성질을 갖고 있는 그래프이다. 예를 들어, 인물 관계도가 있다면 모든 노드는 사람을 의미하는 homogeneity를 갖는다.
Heterogeneous graph는 반대로 그래프의 노드가 여러 종류의 성질을 가지는 그래프이다. 예를 들어 영화-유저 그래프는 어떤 노드는 영화이고, 어떤 노드는 유저를 의미하는 heterogeneity를 갖는다.
Edge-informative Graph
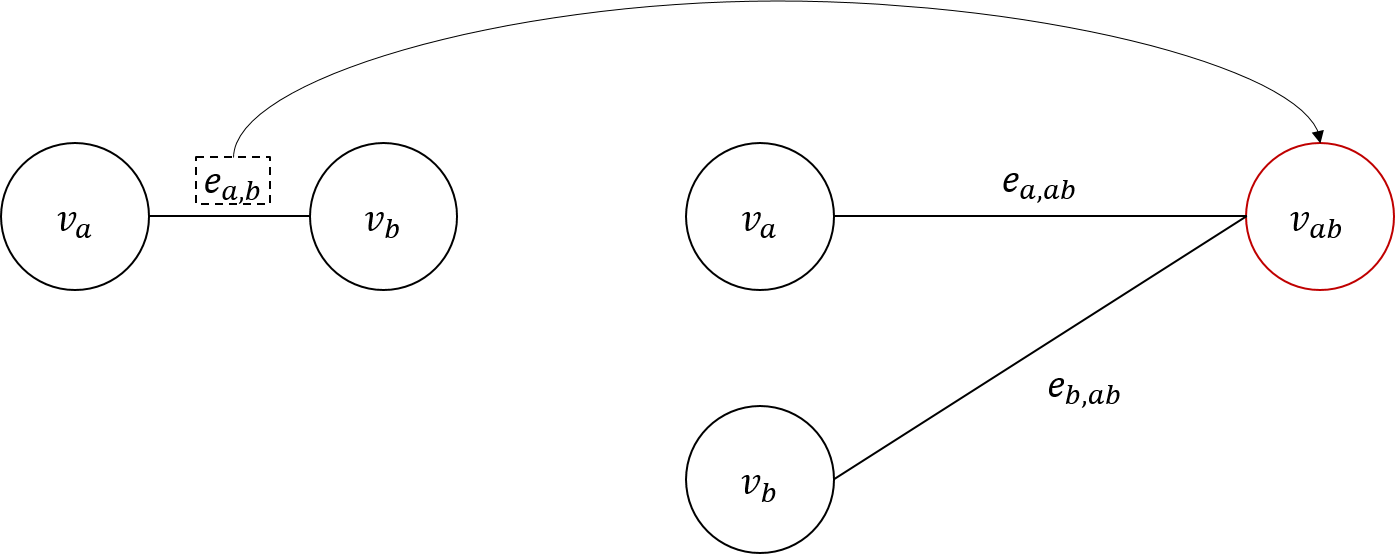
그래프의 각 edge가 가중치를 포함하거나 여러 종류의 성질을 갖는 edge를 포함하는 그래프이다. 이런 경우에는 기존의 edge를 node로 만들어 기존 노드 와 edge 노드 로 나뉘는 bipartite graph를 만들어 그래프를 재구성하여 풀 수 있다. 이 경우에도 임의의 두 노드 사이의 edge는 여러개가 될 수 있다. 친절하게 그림을 그렸다.
Dynamic Graph
Dynamic graph는 그래프의 구조는 같지만 각 node의 feature와 edge feature의 정보가 시시각각 변화하며 들어오는 경우를 말한다. 그래프의 구조는 동일한 시계열 데이터를 해석 해야하는 경우를 말한다. Spatiotemporal analysis를 해야하는데, 어떤 케이스가 있는지는 잘 모르겠다.
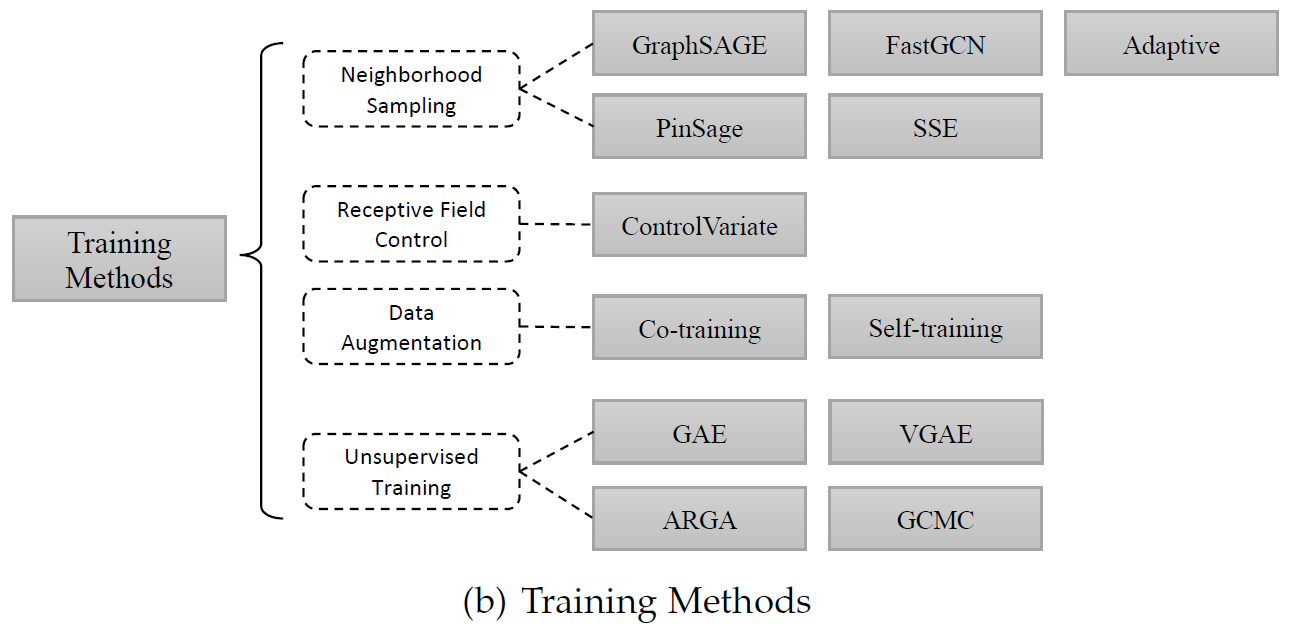
Training Methods에 대한 연구
Neighborhood Sampling
후술하겠지만 Sampling 방식이 아닌(대표적으로 GCN) 방법은 전체 그래프의 Laplacian을 구하는 방법을 사용하는데, 여기에는 큰 문제가 존재한다.
연산량모든 이웃 노드에 대해 gradient를 계산해야만 한다.
확장성새로운 노드가 들어오면 다시금 전체 그래프의 Laplacian을 계산해야 한다.
Inductivity특정 구조의 그래프에 대해 학습하게 되므로 새로운 노드(unlabeled node)가 붙을 경우, unsupervised learning이 어렵다
그래서 이러한 문제를 해결하고자 sampling 방식으로 문제를 해결하려는 연구들이 몇가지 있었다. 요점은전체 그래프를 한번에 고려하는 것보다 샘플링 된 노드를 중심으로 그래프를 해석하면 어떤 구조의 그래프가 들어와도 inductively 해석할 수 있다. 대표적으로 GraphSAGE가 있다.
Receptive Field Control
그래프에서 Receptive Field란 기준 노드로부터 얼마나 멀리 떨어진(k-hop) 노드까지 내 이웃이라고 판단할 것인가 그 범위를 이야기한다.
만약 k가 크다면내 이웃이 그만큼 많다는 이야기이고, 그래프에서 이웃이란 같은 성질을 갖는 set을 의미하게 되므로 graph smoothing이 강하게 일어나게 된다.반면 k가 너무 작다면실제로 이웃인데도 이웃이 아니라고 학습을 해버리는 경향이 강하게 발생하게 된다.이러한 문제를 해결하려면 어떻게 해야할까?
Control Variate를 제안한 논문에서는 1-hop propagation을 채택하여 연산량의 이점을 크게 가져왔다. 하지만 이웃 정보를 한번에 잘 가져오지 못하는 단점을 각 노드 이웃의 이전 layer의 activation 값을 활용하여 이웃을 넓혀가는 방식을 채택하여 보완했다.
Data Augmentation
이 논문에서는 GCN을 학습할 때 labeled data가 많이 필요하다는 점과 전체 그래프의 Laplacian에서 오는 구조적인 제한점을 해결하려고 Co-Training과 Self-Training GCN을 제안했다. 자세한 방법은 나중에 읽어보도록 한다.
Unsupervised Training
이러나저러나 방대한 양의 label된 데이터가 필요하다고 여겨지는데 얻기가 쉽지가 않다. AutoEncoder는 대표적인 unsupervised learning 방법이며 이를 그래프에 적용시켜보면 좋은 결과를 얻을 수 있을 것 같아 시도한 여러 연구들이 존재한다. GC-MC 논문은 추천 알고리즘에서 잘 알려진 matrix completion 방법을 graph-based auto-encoder framework를 통해 더 좋은 결과를 얻었다.
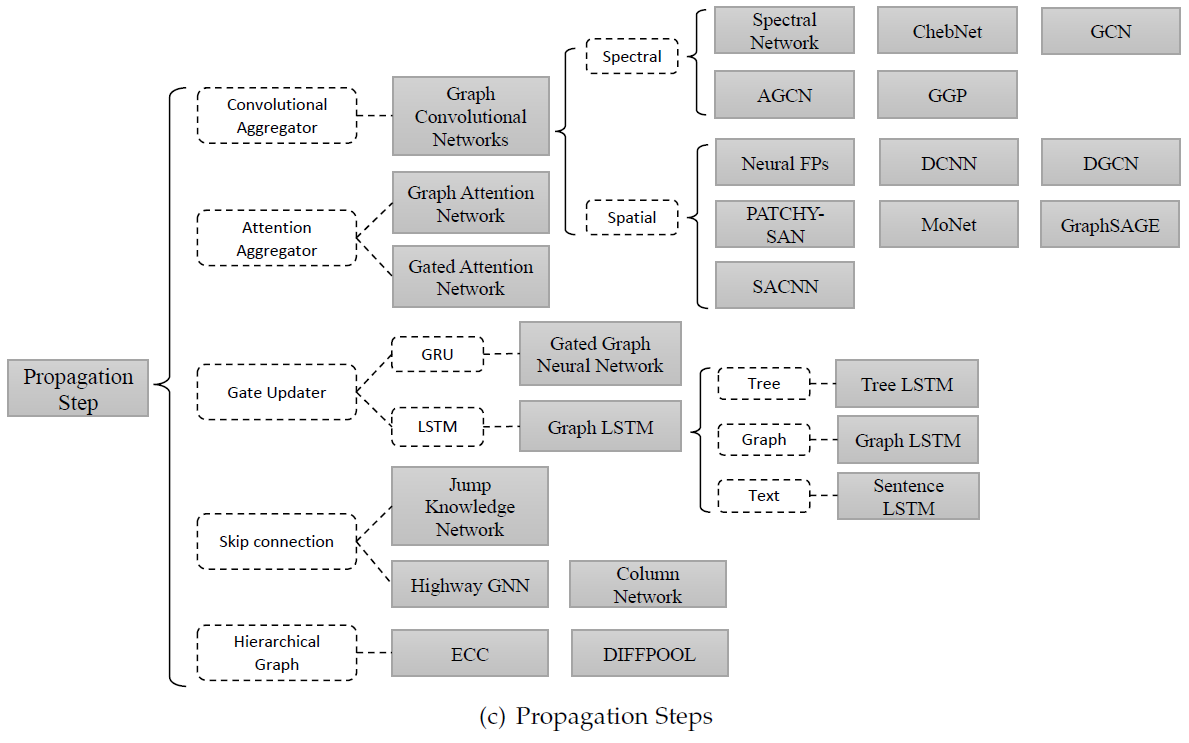
Propagation Types에 대한 연구
이 내용은 상당히 방대한 내용이므로 별도의 포스트에서 다루도록 한다.출처
Zhou, Jie, et al. "Graph neural networks: A review of methods and applications." arXiv preprint arXiv:1812.08434 (2018).