1. Linear Regression

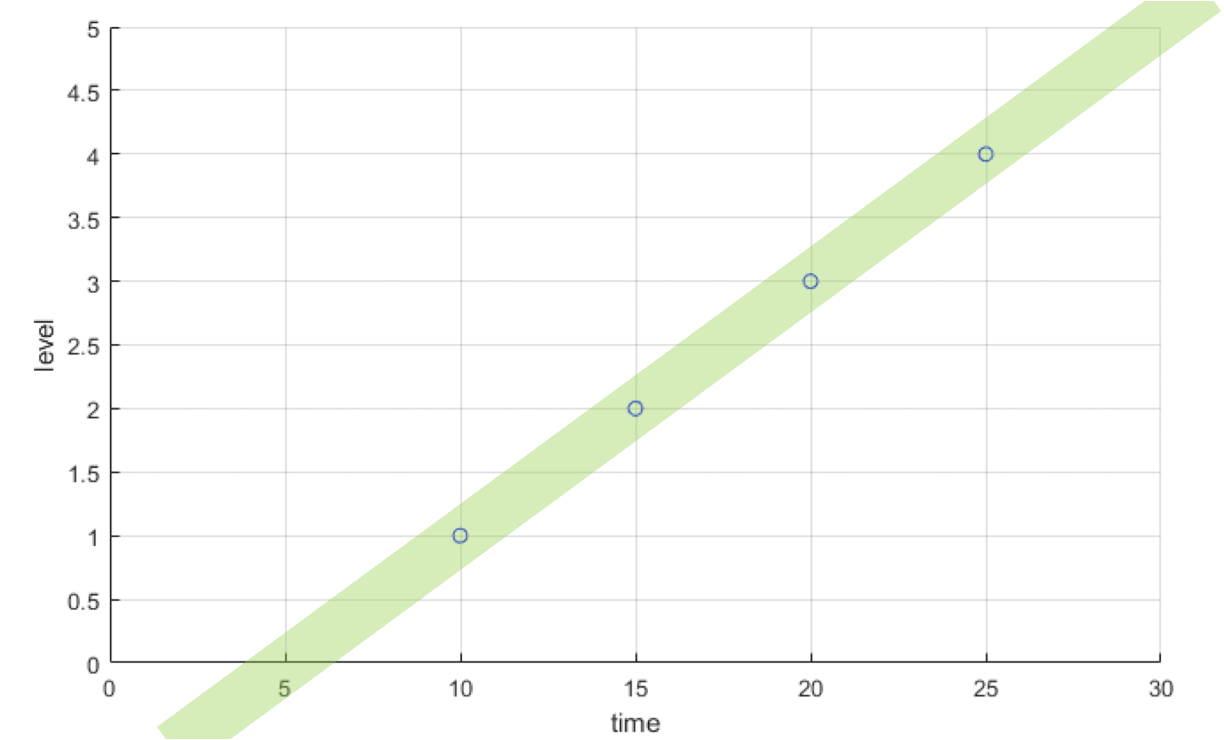
< y = ax + b>

Regression은 data 들의 관계를 분석하는 것이고 data들이 일직선으로 나열되어 있을때 우리는 linear regression을 사용할 수 있다.

2. Hypothesis

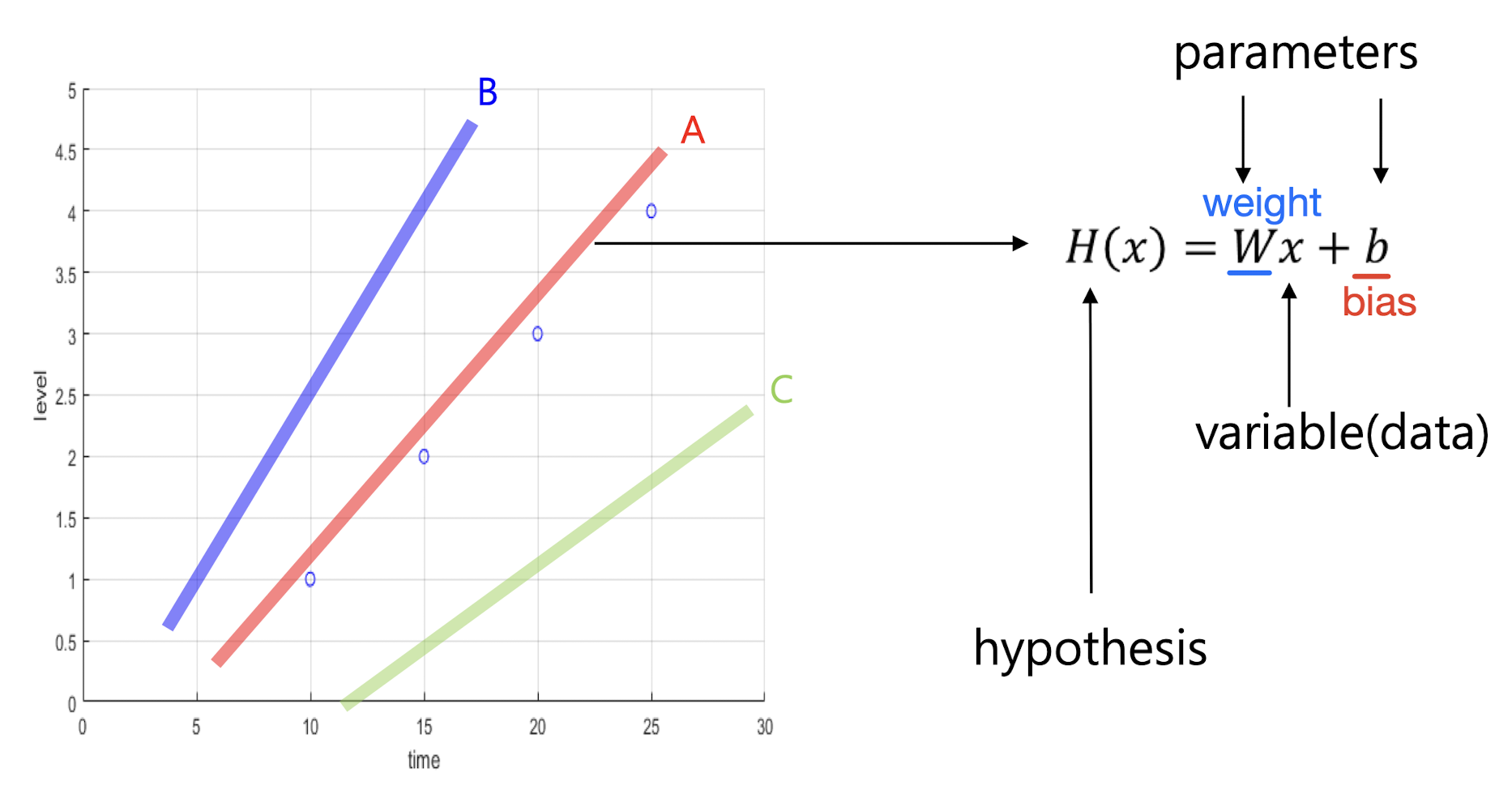
Linear regression 모델을 만드려면 hypothesis가 필요하다. hypothesis는 데이터 분포에 대한 가설이다.

variable(data)는 정해져있고 우리는 오직 parameters만 수정할 수 있다.

3. Cost function

hypothesis가 얼만큼 맞는지 확인해주는 것이 바로 cost function이다. Cost function은 여러가지 방법으로 정의할 수 있는데 Mean Squared Error(MSE)가 주로 사용된다.

우리가 세운 가설이 실제 데이터와 얼마나 다른가를 알기 위해 H(x) - y를 구하고 싶다.

하지만 이 거리는 음수가 될 수도 있기 때문에 제곱을 한 후 평균을 구한다.

⇒ (H(x) - y)^2 평균

Linear Regression의 목표는 cost function의 값이 최소가 되는 W와 b를 구하는 것이다!

4. How to minimize cost function

먼저 b는 무시한다.

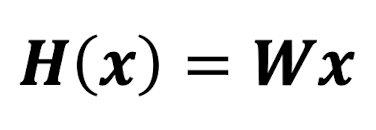
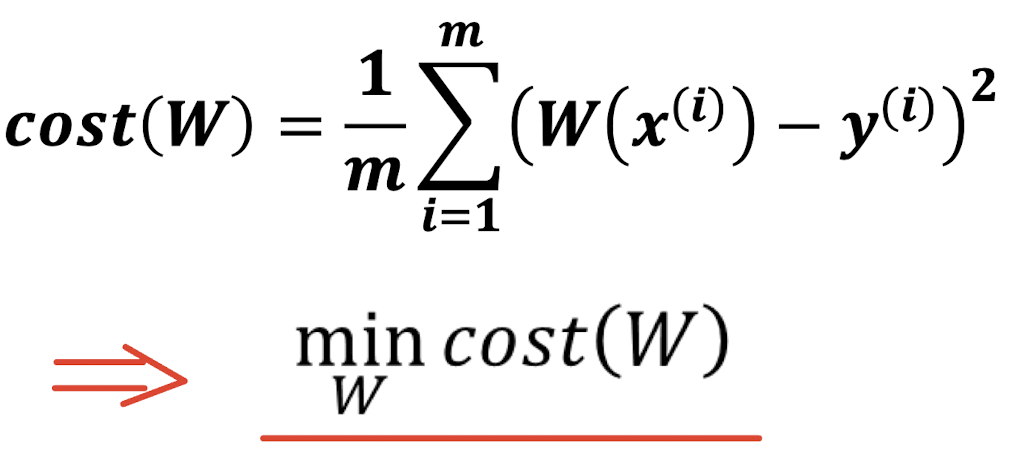
ex)

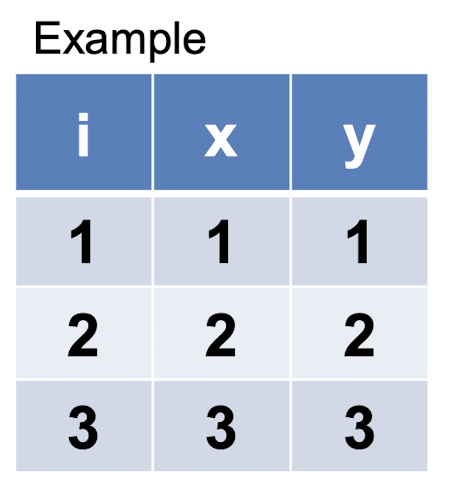
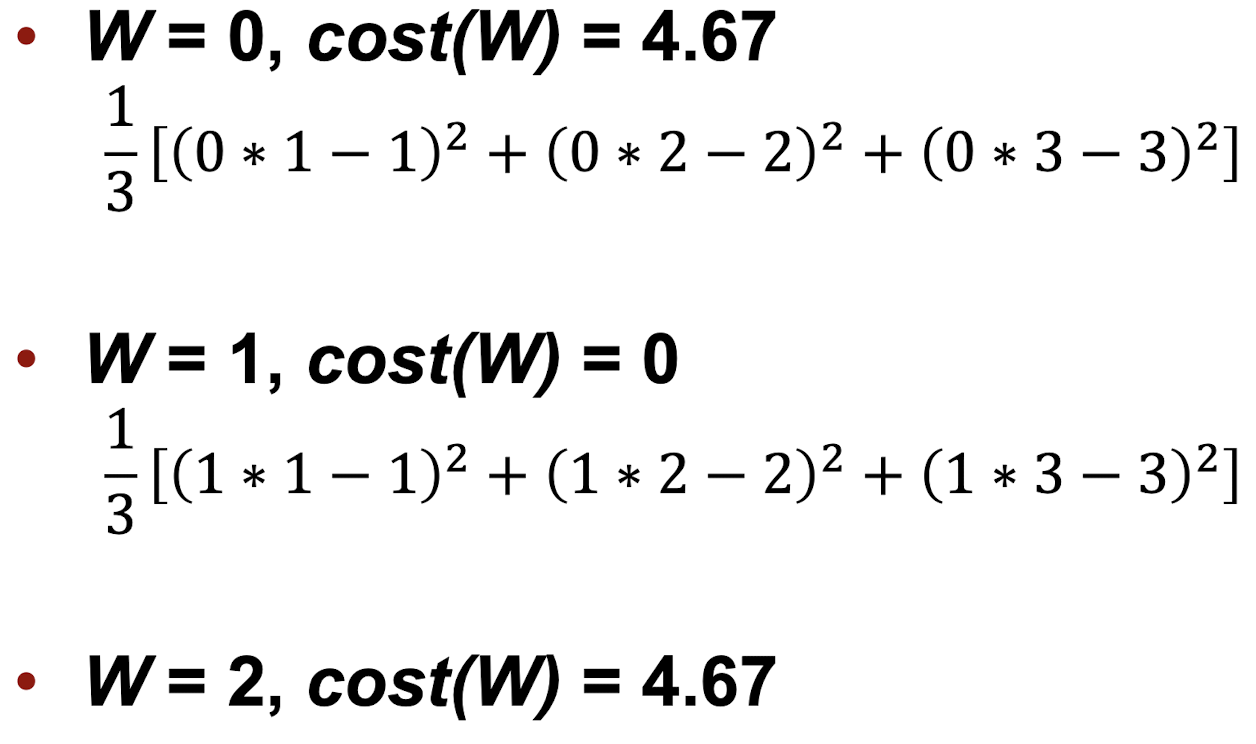
cost값이 떨어지는 방향으로 W를 변경해야 한다. 모든 W에 대한 cost의 최소값을 찾기 위해 Gradient Descent를 사용한다.

w값을 얼만큼 변경할지 정하기 위해 learning rate 값을 지정해주어 학습을 얼마나 할지 설정하고 learning rate값과 기울기 값을 곱한값 만큼을 w에서 뺀다.

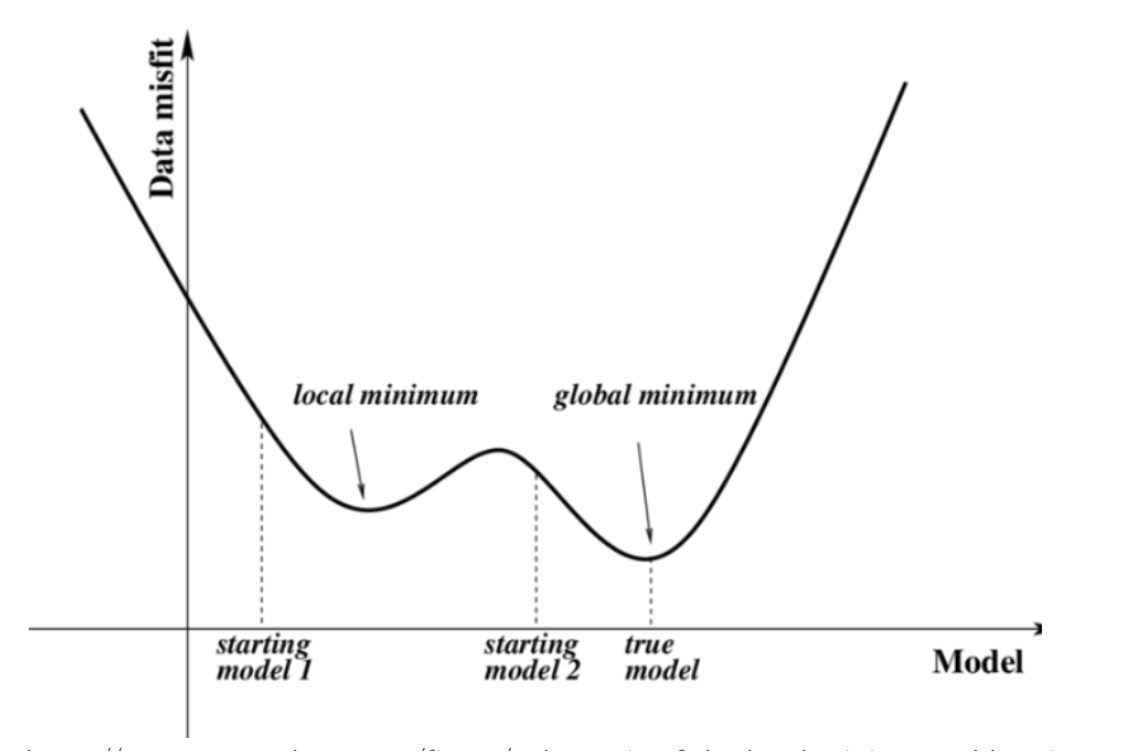
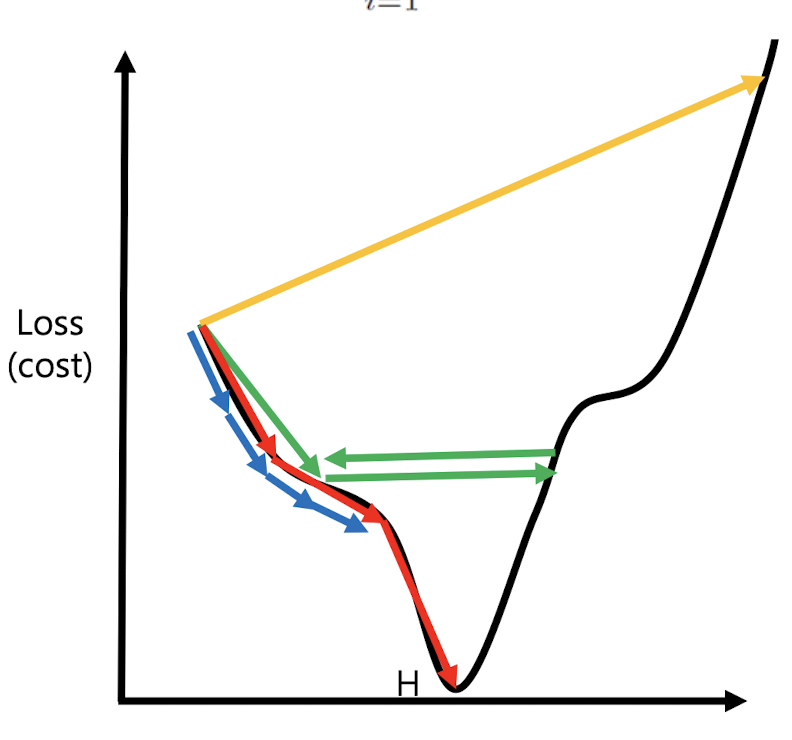
이때 local minima가 아닌 global minima를 찾아야 한다. 그러기 위해서는 cost function이 convex function이라는 보장이 있어야 한다.

그래프가 울퉁불퉁하게 그려지면 local minimum에 빠질 수 있다.

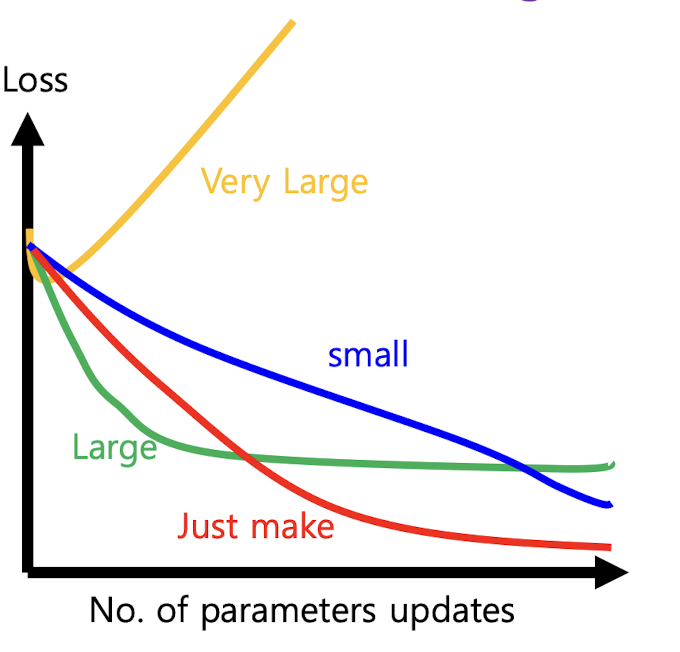
5. Learning Rate

Learning rate은 step size로 hyper parameter중 하나 이다.

⇒ 유저가 직접 개입해서 바꿀 수 있는 parameter이다.
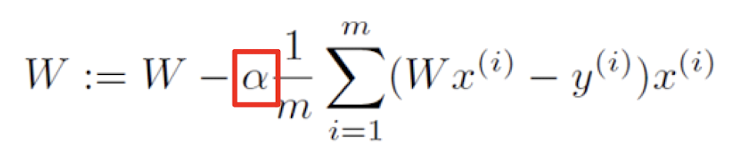