
관계 데이터 모델
관계 데이터 모델 개념
- 데이터의 논리적 구조를 2차원 테이블 형태로 표현하는 모델로, 각 테이블은 튜플과 속성으로 구성
- 기본키와 이를 참조하는 외래키로 데이터 간의 관계 표현
- 계층 모델과 밍 모델의 복잡한 구조를 단순화시킴
- 대표적인 언어 SQL, 1:1, 1:N, N:M 관계를 자유롭게 표현
관계 데이터 릴레이션의 구조⭐️⭐️
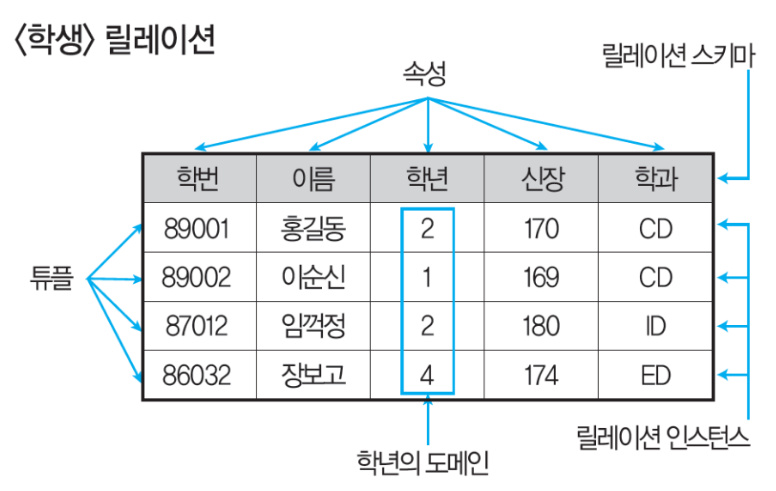
(20.8)
튜플(Tuple), 행(Row), 레코드(Record)
- 속성들의 모임
- 파일 구조상 레코드(실제데이터)를 의미
튜플의 수=카디널리티(Cardinality), 기수, 대응수
속성(Attribute), 열(Column), 필드(Field)
- 데이터베이스를 구성하는 가장 작은 논리적 단위
- 파일 구조상의 데이터 항목 또는 데이터 필드에 해당
- 개체의 특성을 기술
속성의 수=차수(Degree)
속성의 분류
- 기본속성: 업무 분석을 통해 정의(예: 자동차명, 제조일, 연비)
- 설계속성: 설계과정에서 도출(예: 코드, 식별번호)
- 파생속성: 다른 속성값에 기반하여 계산되거나 유도
세부 의미에 다른 분류
- 단순 속성: 다른 속성으로 나뉠 수 없는 기본적인 속성
- 복합 속성: 여러 세부 속성으로 구성될 수 있는 속성(예:시, 구, 동)
개체 구성 방식에 다른 분류
- 기본키 속성: 개체를 식별
- 외래키 속성: 다른 릴레이션의 기본키를 참조
- 일반 속성: 기본키나 외래키가 아닌 속성
속성명 지정 원칙
- 업무에서 사용하는 이름
- 서술식보다는 간결한 이름
- 약어 사용 제한
- 개체명은 속성명으로 사용 불가
- 개체에서 유일하게 식별가능하도록 지정
도메인(Domain)
(20.6)
- 하나의 속성이 가질 수 있는 같은 타입 원자값들의 집합
- 도메인을 정의함으로써 데이터 무결성 유지 가능
- 예: 성별(남, 여), 학년(1~4)
릴레이션
- 데이터들을 2차원 테이블의 구조로 저장한 것
릴레이션의 구성
- 릴레이션 스키마: 릴레이션 이름과 속성 이름을 포함한 릴레이션의 논리적 구조
- 릴레이션 인스턴스: 스키마에 따라 실제로 저장된 데이터의 집합
릴레이션의 특징⭐️
(20.8)
- 튜플 중복 불가
- 튜플 간 순서가 없음
- 속성 간 순서가 없음, 속성의 위치는 중요하지 않음
- 속성은 더이상 분해할 수 없는 원자값을 가져야함
- 속성 중복 불가, 도메인 중복 가능
- 릴레이션은 튜플의 삽입, 갱신, 삭제로 인해 실시간으로 변함
관계 데이터 언어
관계 대수⭐️⭐️⭐️
- 관계형 데이터베이스에서 원하는 데이터를 찾기 위한 절차적 언어
- 데이터를 어떻게(How) 찾아야 하는지의 처리 과정 명시
- 연산의 피연산자와 결과는 모두 릴레이션
- 종류: 순수 관계 연산자, 일반 집합 연산자
어디에 속하는지(20.8)
순수 관계 연산자
SELECT(선택)
- 주어진 조건(Predicate)을 만족하는 튜플들의 부분 집합(수평 연산)
- 표기법:
𝜎<조건>(R) - 조건
- 비교연산자:
=, ≠, <, ≤, >, ≥ - 논리연산자:
∧(AND), ∨(OR), ¬(NOT)
- 비교연산자:
- 예:
𝜎 성적 > 90(학생)𝜎 성적 >= 90 ^ 학과='컴퓨터'(학생)
PROJECT(추출)
- 속성들의 부분 집합, 중복은 제거됨(수직 연산)
- 표기법:
𝜋<리스트>(R) - 예:
𝜋 학번, 성적(학생)𝜋 학번, 성적, 성적(𝜎 성적 >= 90(학생))
JOIN(조인)
(20.6)
- 공통 속성을 이용해 두 릴레이션을 하나로 합쳐 새로운 릴레이션 생성
- 두 릴레이션에서 연관된 튜플들을 결합
- 표기법:
R⨝<조건>S - 예:
(학생) ⨝ 학번=학번 (수강과목)
DIVISION(나누기)
(20.8)
- 릴레이션S의 모든 튜플과 관련있는 릴레이션R의 튜플들을 반환
R÷S
일반 집합 연산자
Union(합집합)
- 두 릴레이션의 튜플 합집합을 구하며, 중복은 제거
- 표기법:
∪
Intersection(교집합)
- 두 릴레이션의 튜플 교집합(중복되는 것들)
- 표기법:
∩
Difference(차집합)
- 한 릴레이션의 튜플에서 다른 릴레이션 튜플을 제거
- 표기법:
-
Cartesian(교차곱)
- 두 릴레이션의 모든 튜플 조합
- 차수는 더하고, 카디널리티는 곱해서 구함
- 표기법:
X
관계 해석⭐️
- 관계 데이터 모델의 제안자인 코드(E.F.Codd)가 수학의 Predicate Calculus(술어 해석)에 기반을 두고 관계 데이터베이스를 위해 제안
- 원하는 정보(What)가 무엇이라는 것만 정의하는 비절차적 특성
- 종류: 튜플 관계해석, 도메인 관계해석
- 관계해석과 관계대수는 처리 능력면에서 동등
- 관계대수로 표현한 식은 관계해석으로 표현 가능
- 질의어로 표현
연산자
- 연산자:
∧(AND), ∨(OR), ¬(NOT) - 정량자
- 전칭 전량자:
∀, 모든 가능한 튜플 "For All" - 존재 정량자:
∃, 어떤 튜플 하나라도 존재 "There Exists"
- 전칭 전량자:
