
Do it! 자료구조와 함께 배우는 알고리즘 입문 | 파이썬편을 읽고 작성된 글입니다.
Github Link : https://github.com/WE-Learning-CS/Data-Structure/tree/main/chap09/02
1. 트리란?
- 데이터 사이의 계층 관계를 표현하는 구조
- 자료구조에서 트리는 부모-자식 관계로 정의하고, 부모에서 자식으로 간선이 이어져있는 유향 그래프를 말한다.
01. 트리의 속성
- 트리는 노드를 포함하지 않거나 0개 이상의 하위 트리가 있는 루트라는 하나의 특수노드를 포함할 수 있다.
- 트리의 모든 가장자리는 루트에서 직접 또는 간접적으로 발생한다.
- 모든 자녀는 부모가 한 명 뿐이지만 한 부모는 여러 자녀를 가질 수 있다.
02. 트리의 구조
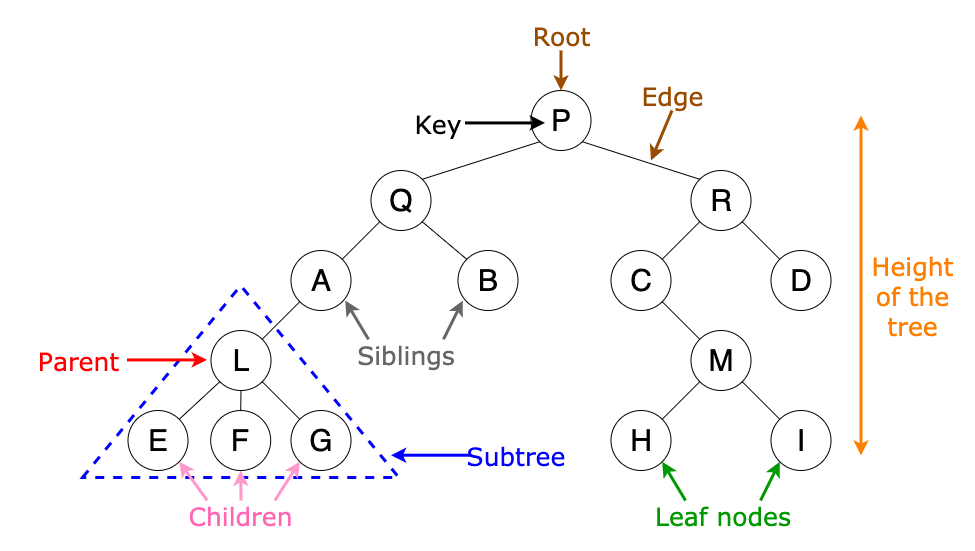
출처 : https://towardsdatascience.com/8-useful-tree-data-structures-worth-knowing-8532c7231e8c
- 루트(Root)
- 트리의 가장 위쪽에 있는 노드
- 루트는 트리 하나에 1개만 존재한다.
- 리프(leaf)
- 트리의 가장 아래쪽에 있는 노드
- 단말노드(terminal node)또는 외부 노드(external node)라고도 한다.
- 물리적으로 가장 밑에 위치한다는 의미가 아니라 가지가 더이상 뻗어나갈 수 없는 마지막에 노드가 있다는 뜻
- 비단말 노드(non-terminal node)
- 리프를 제외한 노드(루트는 포함)
- 또는 내부노드(internal node)라고도 한다.
- 부모(parent)
- 어떤 노드와 가지가 연결되었을 때 가장 위쪽에 있는 노드
- 노드의 부모는 하나뿐
- 루트는 부모 노드를 갖지 않는다
- 자식(child)
- 어떤 노드와 가지가 연결되었을 때 아래쪽 노드
- 노드는 자식을 몇개라도 가질 수 있다
- 가장 아래쪽의 리프는 자식을 갖지 않는다
- 형제(siblings)
- 부모가 같은 노드
- 조상(ancester)
- 어떤 노드에서 위쪽으로 가지를 따라가면 만나는 모든 노드
- 자손(descendant)
- 어떤 노드에서 아래쪽으로 가지를 따라가면 만나는 모든 노드
- 레벨(level)
- 루트에서 얼마나 멀리 떨어져있는지를 나타내는 것
- 루트의 레벨은 0이고, 가지가 하나씩 아래로 뻗어 내려갈때마다 레벨이 1씩 증가
- 차수(degree)
- 각 노드가 갖는 자식의 수
- 모든 노드의 차수가 n이하인 트리를 n진 트리(그림은 3진 트리)
- 높이(height)
- 루트에서 가장 멀리 있는 리프까지의 거리
- 리프 레벨의 최댓값(그림의 높이는 4)
- 서브 트리(subtree)
- 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리
- 빈 트리
- 노드와 가지가 전혀 없는 트리
- 널 트리(null tree)라고도 한다.
2. 순서 트리와 무순서 트리

출처 : https://www.geeksforgeeks.org/combinatorics-ordered-trees/
- 순서 트리(ordered tree)
- 무순서 트리(unordered tree) : 형제 노드의 순서 구별이 없는 트리 (T2)
01. 순서 트리의 검색

순서 트리의 노드를 스캔하는 방법은 크게 다음 2가지 이다.
- 너비 우선 검색(breadth-first search)
- 깊이 우선 검색(depth-first search)
너비 우선 검색
폭 우선 검색, 가로 검색, 수평 검색이라고도 한다.
- 낮은 레벨부터 왼쪽에서 오른쪽으로 검색하고, 한 레벨에서 검색을 마치면 다음 레벨로 내려가는 방법
- 맹목적 탐색방법의 하나로 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법
- 더이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 너비 우선 검색을 적용한다.
사진에서 BFS를 검색하는 순서는 다음과 같다
F → B → G→ A →D → I → C→ E→ H
코드
# 출처 : https://favtutor.com/blogs/breadth-first-search-python
graph = {
'5' : ['3','7'],
'3' : ['2', '4'],
'7' : ['8'],
'2' : [],
'4' : ['8'],
'8' : []
}
visited = [] # List for visited nodes.
queue = [] #Initialize a queue
def bfs(visited, graph, node): #function for BFS
visited.append(node)
queue.append(node)
while queue: # Creating loop to visit each node
m = queue.pop(0)
print (m, end = " ")
for neighbour in graph[m]:
if neighbour not in visited:
visited.append(neighbour)
queue.append(neighbour)
# Driver Code
print("Following is the Breadth-First Search")
bfs(visited, graph, '5') # function callingBFS 장/단점
장점
- 출발 노드에서 목표 노드까지의 최단 길이 경로를 보장한다.
단점
- 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
- 해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
- 무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.
깊이 우선 검색

세로 검색, 수직 검색이라고도 한다.
- 리프에 도달할 때 까지 아래쪽으로 내려가면서 검색하는 것을 우선으로 하는 방법
- 리프에 도달해서 검색할 곳이 없으면 일단 부모 노드로 돌아가고 그 뒤 다시 자식 노드로 내려간다.
깊이 우선 검색은 다음과 같이 세 종류의 스캔 방법으로 구분한다.
전위 순회(preorder)
전위 순회는 다음과 같은 순서로 스캔한다.
노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
위의 사진에서 트리 전체 스캔은 다음과 같이 진행한다.
F -> B -> A -> D -> C -> E -> G -> I -> H
중위 순회(inorder)
중위 순회는 다음과 같은 순서로 스캔한다.
왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
위의 사진에서 트리 전체 스캔은 다음과 같이 진행한다.
A -> B -> C -> D -> E -> F -> H -> I -> G
후위 순회(postorder)
후위 순회는 다음과 같은 순서로 스캔한다.
왼쪽 자식 -> 오른쪽 자식 -> 노드 방문
위의 사진에서 트리 전체 스캔은 다음과 같이 진행한다.
A -> C -> E -> D -> B -> H -> I -> G -> F
DFS 장/단점
장점
- 단지 현 경로상의 노드들만을 기억하면 되므로 저장공간의 수요가 비교적 적다
- 목표 노드가 깊은 단게에 있을 경우 해를 빨리 구할 수 있다.
단점
- 해가 없는 경로에 깊이 빠질 가능성이 있다. 따라서 실제의 경우 미리 지정한 임의의 깊이까지만 탐색하고 목표노드를 발견하지 못하면 다음의 경로를 따라 탐색하는 방법이 유용할 수 있다.
- 얻어진 해가 최단 경로가 된다는 보장이 없다. 이는 목표에 이르는 경로가 다수인 문제에 대해 깊이우선 탐색은 해에 다다르면 탐색을 끝내버리므로, 이때 얻어진 해는 최적이 아닐 수 있다는 의미이다.
코드
# 출처 : https://favtutor.com/blogs/depth-first-search-python
# Using a Python dictionary to act as an adjacency list
graph = {
'5' : ['3','7'],
'3' : ['2', '4'],
'7' : ['8'],
'2' : [],
'4' : ['8'],
'8' : []
}
visited = set() # Set to keep track of visited nodes of graph.
def dfs(visited, graph, node): #function for dfs
if node not in visited:
print (node)
visited.add(node)
for neighbour in graph[node]:
dfs(visited, graph, neighbour)
# Driver Code
print("Following is the Depth-First Search")
dfs(visited, graph, '5')
03. 이진 트리
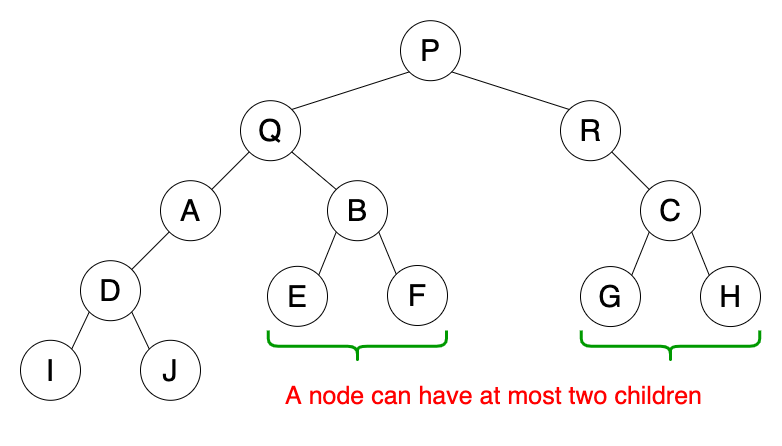
노드가 왼쪽 자식과 오른쪽 자식만을 갖는 트리를 이진트리라고 한다.
이때 두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관 없다.
이진 트리의 특징
- 왼쪽 자식과 오른쪽 자식을 구분한다.
- 노드는 최대 두개의 하위 노드(자식)을 가질 수 있다.
- 왼쪽 자식 노드는 부모 노드보다 값이 적어야 한다.
- 오른쪽 자식 노드는 부모 노드보다 값이 커야한다.
이진 트리의 시간 복잡도
이진트리는 일반적으로 빠른 검색을 위해서 사용된다.
정렬이 된 array가 O(N)인 반면 이진 트리는 O(log n)이다.
01. 완전 이진 트리

루트부터 아래쪽 레벨로 노드가 가득 차 있고, 같은 레벨 안에서 왼쪽부터 오른쪽으로 노드가 채워져 있는 이진 트리를 완전 이진 트리(complete binary tree)라고 한다.
높이가 k인 완전 이진 트리가 가질 수 있는 노드의 수는 최대 2^k+1 - 1개 이므로 n개의 노드를 저장할 수 있는 완전 이진 트리의 높이는 log n이다.
완전 이진 트리의 노드를 채우는 법
- 마지막 레벨을 제외하고 모든 레벨에 노드가 가득 차 있다.
- 마지막 레벨에 한해서 왼쪽부터 오른쪽으로 노드를 채우되, 반드시 끝까지 채우지 않아도 된다.
02. 균형 검색 트리
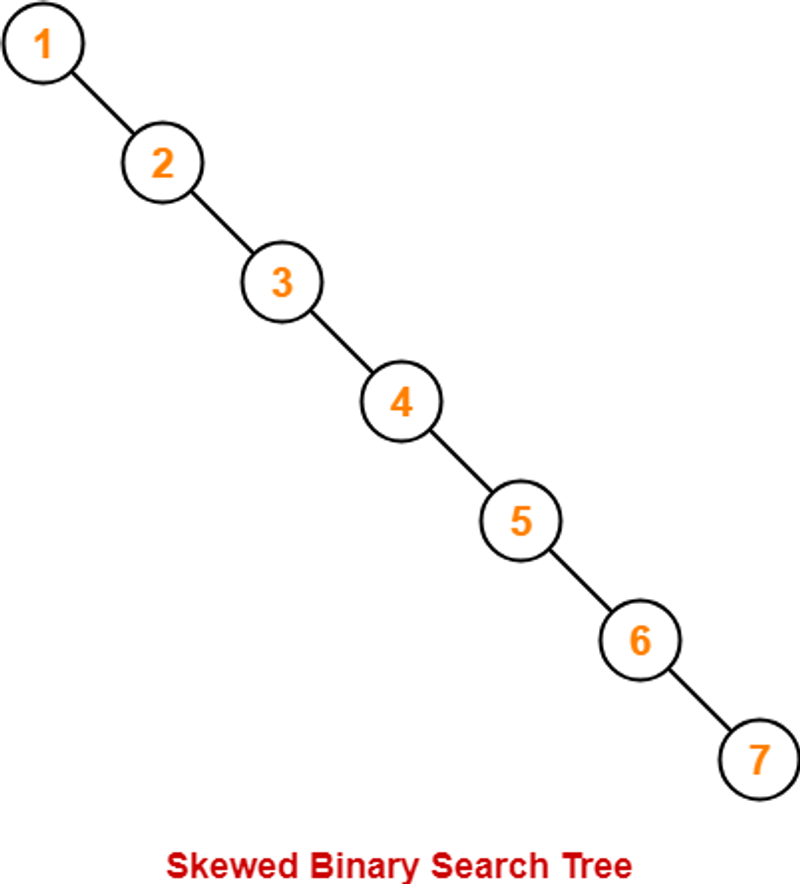
이진 검색트리는 위 사진 처럼키의 오름차순으로 노드가 삽입되면 트리의 높이가 깊어지는 단점이 있다.(데이터가 이미 정렬되어 있는 경우)
이럴 경우 선형 리스트 처럼 되어 빠른 검색을 할 수 없어 시간 복잡도가 O(n)이 나올 수 있다.
이를 방지하고자 높이를 O(log n)으로 제한하여 고안된 검색 트리를 균형 검색 트리라고 하고 다음과 같은 종류가 있다.
- AVL 트리(AVL tree)
- 레드 - 블랙 트리 (red-black tree)
레드 - 블랙 트리(RBtree)

레드 - 블랙 트리는 항상 다음 규칙을 준수해야 한다.
- 모든 노드는
레드이거나블랙이어야 한다. - 루트 노드는 항상
블랙이어야 한다. - 리프 노드도 항상
블랙이어야 한다. 레드노드는 연달아 나올 수 없다.레드노드의 부모는 항상블랙노드여야하고, 자식 노드들도블랙노드여야 한다.블랙노드의 자식은블랙일 수 있다.
- 루트 노드와 모든 리프 노드 사이에 존재하는
블랙노드의 수는 모두 동일하다.
04. 이진 검색 트리
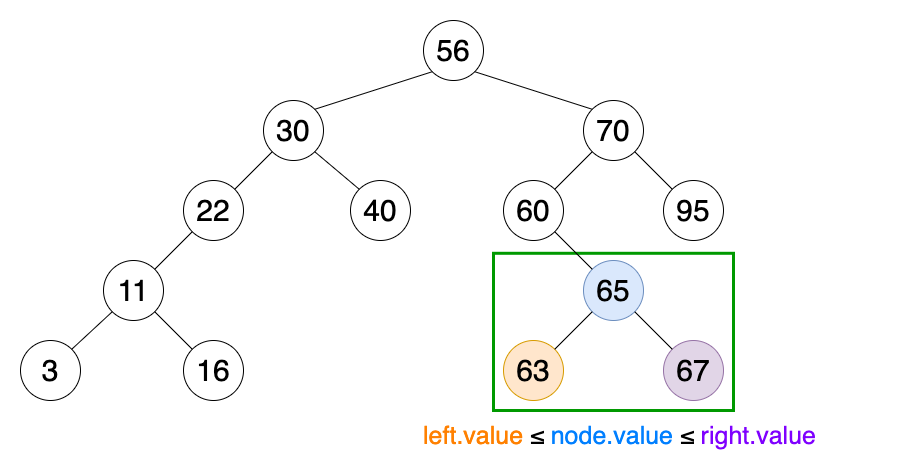
이진 검색 트리는 모든 노드가 다음 조건을 만족해야 한다.
- 왼쪽 서브트리 노드의 키 값은 자신의 노드 키값보다 작아야한다.
- 오른쪽 서브트리 노드의 키 값은 자신의 노드 키 값보다 커야 한다.
이진 검색 트리의 특징
- 구조가 단순하다
- 중위 순회의 깊이 우선 검색을 통하여 노드 값을 오름차순으로 얻을 수 있다.
- 이진 검색과 비슷한 방식으로 아주 빠르게 검색할 수 있다.
- 노드를 삽입하기 쉽다.
01. 이진 검색 트리 구현하기
노드 클래스 Node
from __future__ import annotations
from typing import Any, Type
class Node:
'''이진 검색 트리의 노드'''
def __init__(self, key: Any, value: Any, left: Node = None, right: Node = None):
self.key = key
self.value = value
self.left = left
self.right = right
- key : 키(임의의 형)을 나타낸다
- value : 값(임의의 형)을 나타낸다
- left : 왼쪽 자식 노드에 대한 참조(왼쪽 포인터)를 나타낸다
- right : 오른쪽 자식 노드에 대한 참조(오른쪽 포인터)를 나타낸다
이진 검색 클래스 BinarySearchTree
class BinarySearchTree:
'''이진 검색 트리'''
def __init__(self):
self.root = None # 루트- root : 루트에 대한 참조를 유지하는 필드
키값으로 노드를 검색하는 search()함수
- 루트에 주목한다. 여기서 주목하는 노드는 p
- p가 None이면 검색을 실패하고 종료한다.
- 검색하는 key와 주목 노드 p의 키를 비교한다.
- key == p : 검색을 성공하고 종료
- key > p : 주목 노드를 오른쪽 자식 노드로 옮김
- key < p : 주목 노드를 왼쪽 자식 노드로 옮김
- 2번 과정으로 되돌아 간다.
def search(self, key: Any) -> Any:
'''키가 key인 노드를 검색'''
p = self.root # 루트 주목
while True:
if p is None: # 더이상 진행할 수 없으면
return None # 검색 실패
if key == p.key : # key와 노드 p의 키가 같으면
return key.value # 검색 성공
elif key < p.key : # key쪽이 작으면
p = p.left # 왼쪽 서브 트리에서 검색
else : # key 쪽이 크면
p = p.right # 오른쪽 서브 트리에서 검색검색 성공
위의 사진에서 키 값이 7인 노드를 검색하여 성공하는 과정은 다음과 같다.
- 처음에 주목하는 루트의 키는 8이다. 8은 7보다 크므로 왼쪽 자식 노드를 따라간다.
- 다음에 주목하는 노드의 키는 3이다. 3은 7보다 작으므로 오른쪽 자식 노드를 따라간다.
- 다음에 주목하는 노드의 키는 6이다. 6은 7보다 작으므로 오른쪽 자식 노드를 따라간다.
- 키가 7인 노드에 도달했으므로 검색에 성공한다.
검색 실패
위의 사진에서 키 값이 11인 노드를 검색하여 실패하는 과정은 다음과 같다.
- 처음에 주목하는 루트의 키는 8이다. 8은 11보다 작으므로 오른쪽 자식 노드를 따라간다.
- 다음에 주목하는 노드의 키는 10이다. 10은 11보다 작으므로 오른쪽 자식 노드를 따라간다.
- 다음에 주목하는 노드의 키는 14이다. 14는 11보다 크므로 왼쪽 자식 노드를 따라간다.
- 다음에 주목하는 노드의 키는 13이다. 주목 노드는 리프이고 오른쪽 자식 노드는 존재하지 않는다. 더이상 스캔을 할 수 없으므로 검색에 실패한다.
노드를 삽입하는 add()함수
노드를 삽입한 뒤에 트리의 형태가 이진 검색 트리의 조건을 유지해야 한다.
따라서 노드를 삽입할 때에는 검색할 때와 마찬가지로 먼저 삽입할 위치를 찾아낸 뒤에 수행해야 한다.
- 루트에 주목한다. 여기서 주목하는 노드는 node
- 삽입하는 key와 주목 node의 키를 비교한다.
- key == node : 삽입을 실패하고 종료한다.
- key < node
- 왼쪽 자식 노드가 없으면 그 자리에 노드를 삽입하고 종료한다.
- 왼쪽 자식 노드가 있으면, 주목 노드를 왼쪽 자식 노드로 옮긴다
- key > node
- 오른쪽 자식 노드가 없으면 그 자리에 노드를 삽입하고 종료한다.
- 오른쪽 자식 노드가 있으면, 주목 노드를 오른쪽 자식 노드로 옮긴다
- 2번 과정으로 되돌아간다.
def add(self, key: Any, value: Any) -> bool:
'''키가 key이고 값이 value인 노드를 삽입'''
def add_node(node: Node, key: Any, value: Any) -> None:
'''node를 루트로 하는 서브트리에 키가 key이고 값이 value인 노드를 삽입'''
if key == node.key:
return False # key가 이진 검색 트리에 이미 존재
elif key < node.key:
if node.left is None:
node.left = Node(key, value, None, None)
else:
add_node(node.left, key, value)
elif key > node.key:
if node.right is None:
node.right = Node(key, value, None, None)
else:
add_node(node.right, key, value)
return True
if self.root is None:
self.root = Node(key, value, None, None)
return True
else:
return add_node(self.root, key, value)삽입 성공
위의 사진에서 키 값이 15인 노드를 삽입하여 성공하는 과정은 다음과 같다.
- 삽입할 위치를 찾는다. 추가할 값 15는 14 보다 크고 오른쪽 자식 노드가 존재하지 않으므로 삽입할 위치로 14를 선택한다.
- 15를 오른쪽 자식 노드로 삽입한다.
노드를 삭제하는 remove()함수
노드를 삭제할때는 다음 3가지 경우가 존재한다.
- 자식 노드가 없는 노드를 삭제하는 경우
- 자식 노드가 1개인 노드를 삭제하는 경우
- 자식 노드가 2개인 노드를 삭제하는 경우
자식 노드가 없는 노드를 삭제하는 경우
- 삭제할 노드가 부모 노드의 왼쪽 자식인 경우 : 부모의 왼쪽 포인터를 None으로 한다.
- 삭제할 노드가 부모 노드의 오른쪽 자식인 경우 : 부모의 오른쪽 포인터를 None으로 한다.
자식 노드가 1개인 노드를 삭제하는 경우
- 삭제할 노드가 부모 노드의 왼쪽 자식인 경우 : 부모의 왼쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트 한다.
- 삭제할 노드가 부모 노드의 오른쪽 자식인 경우 : 부모의 오른쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트 한다.
자식 노드가 2개인 노드를 삭제하는 경우
- 삭제할 노드의 왼쪽 서브트리에서 키 값이 가장 큰 노드를 검색한다.
- 검색한 노드를 삭제 위치로 옮긴다. 즉, 검색한 노드의 데이터를 삭제할 노드 위치에 복사한다.
- 옮긴 노드를 삭제한다. 이때 자식 노드의 개수에 따라 다음을 수행한다.
- 옮긴 노드에 자식이 없으면 :
자식 노드가 없는 노드의 삭제에 따라 노드를 삭제한다. - 옮긴 노드에 자식이 있으면 :
자식 노드가 1개인 노드의 삭제에 따라 노드를 삭제한다.
- 옮긴 노드에 자식이 없으면 :
def remove(self, key: Any) -> bool:
'''키가 key인 노드를 삭제'''
p = self.root # 스캔중인 노드
parent = None # 스캔 중인 노드의 부모 노드
is_left_child = True # p는 parent의 왼쪽 자식 노드인지 확인
while True:
if p is None: # 더이상 진행할 수 없으면
return False # 그 키는 존재하지 않음
if key == p.key: # key와 자식 노드 p의 키가 같으면
break # 검색 성공
else:
parent = p # 가지를 내려가기 전에 부모를 설정
if key < p.key: # key쪽이 작으면
is_left_child = True # 여기서 내려가는 것은 왼쪽 자식
p = p.left # 왼쪽 서브트리에서 검색
else: # key쪽이 크면
is_left_child = False # 여기서 내려가는 것은 오른쪽 자식
p = p.right # 오른쪽 서브 트리에서 검색
if p.left is None: # p 왼쪽에 자식이 없으면
'''자식 노드가 없는 노드를 삭제하는 경우와
자식 노드가 1개인 노드를 삭제하는 경우'''
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right # 부모의 왼쪽 포인터가 오른쪽 자식을 가리킴
else:
parent.right = p.right # 부모의 오른쪽 포인터가 오른쪽 자식을 가리킴
elif p.right is None: # p에 오른쪽 자식이 없으면
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left # 부모의 왼쪽 포인터가 왼쪽 자식을 가리킴
else:
parent.right = p.left # 부모의 오른쪽 포인터가 왼쪽 자식을 가리킴
else:
'''자식 노드가 2개인 노드를 삭제하는 경우'''
parent = p
left = p.left # 서브트리 안에서 가장 큰 노드
is_left_child = True
while left.right is not None: # 가장 큰 노드 left를 검색
parent = left
left = left.right
is_left_child = False
p.key = left.key # left의 키를 p로 이동
p.value = left.value # left의 데이터를 p로 이동
if is_left_child:
parent.left = left.left # left를 삭제
else:
parent.right = left.left # left를 삭제
return True

