디즈니에서 연구한 Semanic Deep Face Models 입니다.
https://www.youtube.com/watch?v=awnqYKNJamU&ab_channel=DisneyResearchHub
https://studios.disneyresearch.com/2020/11/25/semantic-deep-face-models/
Abstract
Face models built from 3D face databases are often used in computer vision and graphics tasks such as face reconstruction, replacement, tracking and manipulation. For such tasks, commonly used multilinear morphable models, which provide semantic control over facial identity and expression, often lack quality and expressivity due to their linear nature. Deep neural networks offer the possibility of non-linear face modeling, where so far most research has focused on generating realistic facial images with less focus on 3D geometry, and methods that do produce geometry have little or no notion of semantic control, thereby limiting their artistic applicability. We present a method for nonlinear 3D face modeling using neural architectures that provides intuitive semantic control over both identity and expression by disentangling these dimensions from each other, essentially combining the benefits of both multi-linear face models and nonlinear deep face networks. The result is a powerful, semantically controllable, nonlinear, parametric face model. We demonstrate the value of our semantic deep face model with applications of 3D face synthesis, facial performance transfer, performance editing, and 2D landmark-based performance retargeting.
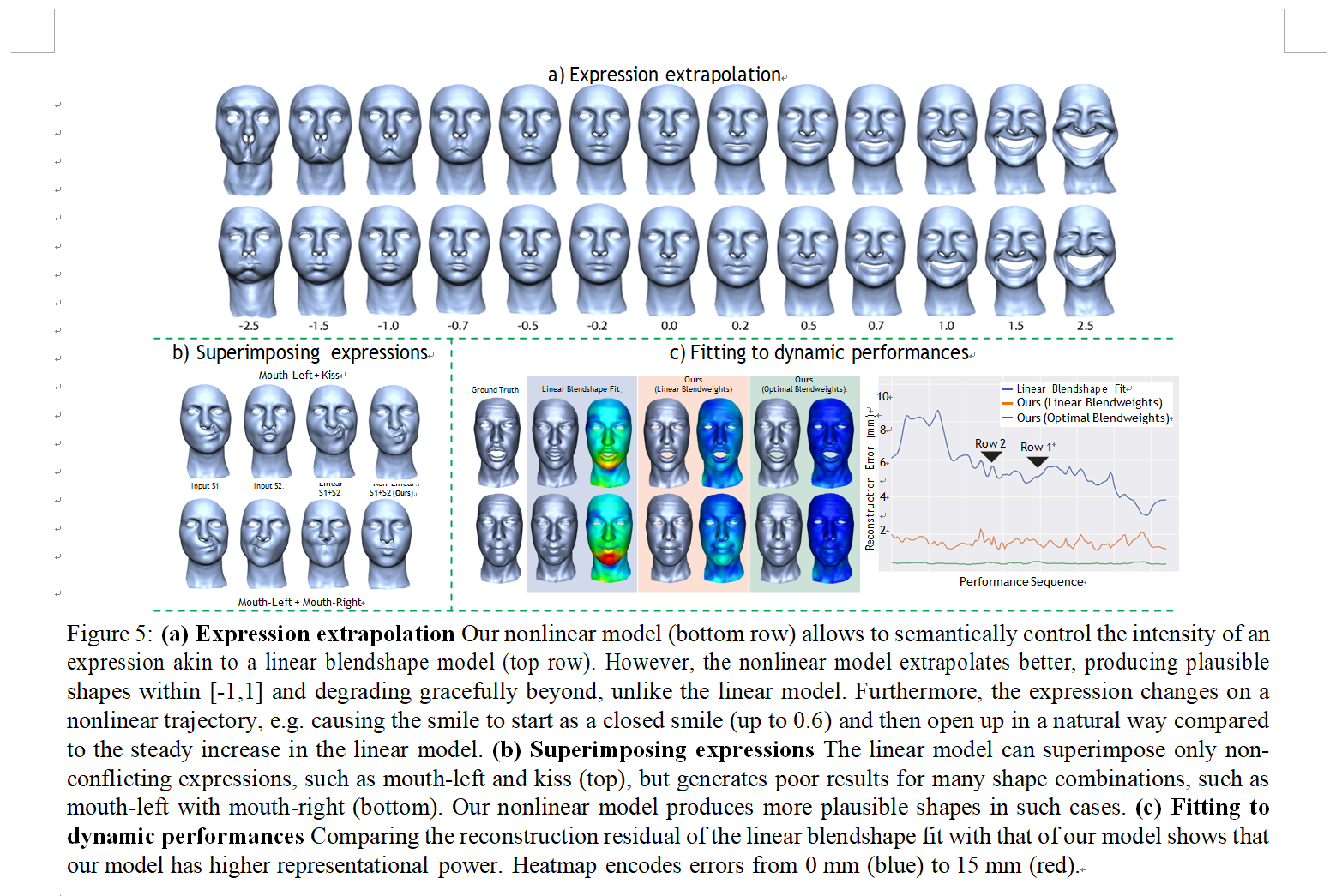
Data-driven face models are very popular in computer vision and computer graphics, as they can aid in several important challenges like model-based 3D face tracking [12], facial performance retargeting [29], video based reenactment [32], and image editing [6]. These models are built from large databases of facial scans. Most commonly, linear face models are built, where the approximated face is expressed as a linear combination of the dataset shapes [7]. Extensions to multilinear models [13, 33] also exist, which generate a tensor of different semantic dimensions (e.g. identity and expression). This ability to have semantic separation of attributes has several benefits, including for example constrained face fitting (e.g. fitting to an identity while constraining to the neutral expression, or fitting to an expression once the identity is known), performance animation (e.g. modifying only the expression space of the model), performance transfer or retargeting (modifying only the identity space of the model), etc. In general a model that provides semantic separation lends itself better to artistic control. The main problem with traditional mod- els, however, is their linearity. The human face is highly nonlinear in its deformation, and it is well known that a simple blending of static expressions often results in unrealistic motion. In severe cases, many combinations of the input expressions can lead to physically impossible face shapes (see Fig. 5). To summarize, linear models constrain the space of shapes to a manifold which on the one hand usually cannot represent all possible face shapes, and on the other hand can easily represent many non-face shapes.
As we shall see in more detail in Section 2, recent methods have begun to investigate nonlinear face models using neural networks [28, 1, 14, 20, 16, 24, 3], which can, to some degree, overcome the limitations of linear models. Unfortunately, some of these approaches have thus far sacrificed the human interpretable nature of multi-linear models, as one typically loses semantics when moving to a latent space learned by a deep network.
In this work, we aim to combine the benefits of multi-linear and neural face models by proposing a new architecture for semantic deep face models. Our goal is to retain the same semantic separation of identity and expression as with multi-linear models, but with deep variational networks that allow nonlinear expressiveness. To this end, we propose a network architecture that takes the neutral 3D geometry of a subject, together with a target expression, and learns to deform the subject’s face into the desired expression. This is done in a way that fully disentangles the latent space of facial identities from the latent space of expressions. As opposed to existing deep methods [1, 14, 20, 16], the disentanglement is explicitly factored into our architecture and not learned. As a consequence, our method achieves perfect disentanglement between facial identity and expression in its latent space, while still encoding the correlation between identity and expression in shape space, i.e. the shape change induced by an expression differs as a function of the identity shape. Once trained (end to end), one can traverse the identity latent space to synthesize new 3D faces, and traverse the expression latent space to generate new 3D expressions, all with nonlinear behavior. Furthermore, since we condition the expression based on the popular represen- tation of linear blendshape weights, the resulting network allows for semantic exploration of the expression space, which is also lacking in existing methods.
As face models that generate geometry alone have limited applicability, we further incorporate the appearance of the face into our architecture, in the form of a diffuse albedo texture map. An initial per-vertex color prediction that corresponds to the face geometry is transferred to the UV domain resulting in an low resolution texture map. We employ an image to image translation network [34] as a residual super-resolution network to transform the initial low resolution albedo to a resolution of 1024 x 1024.
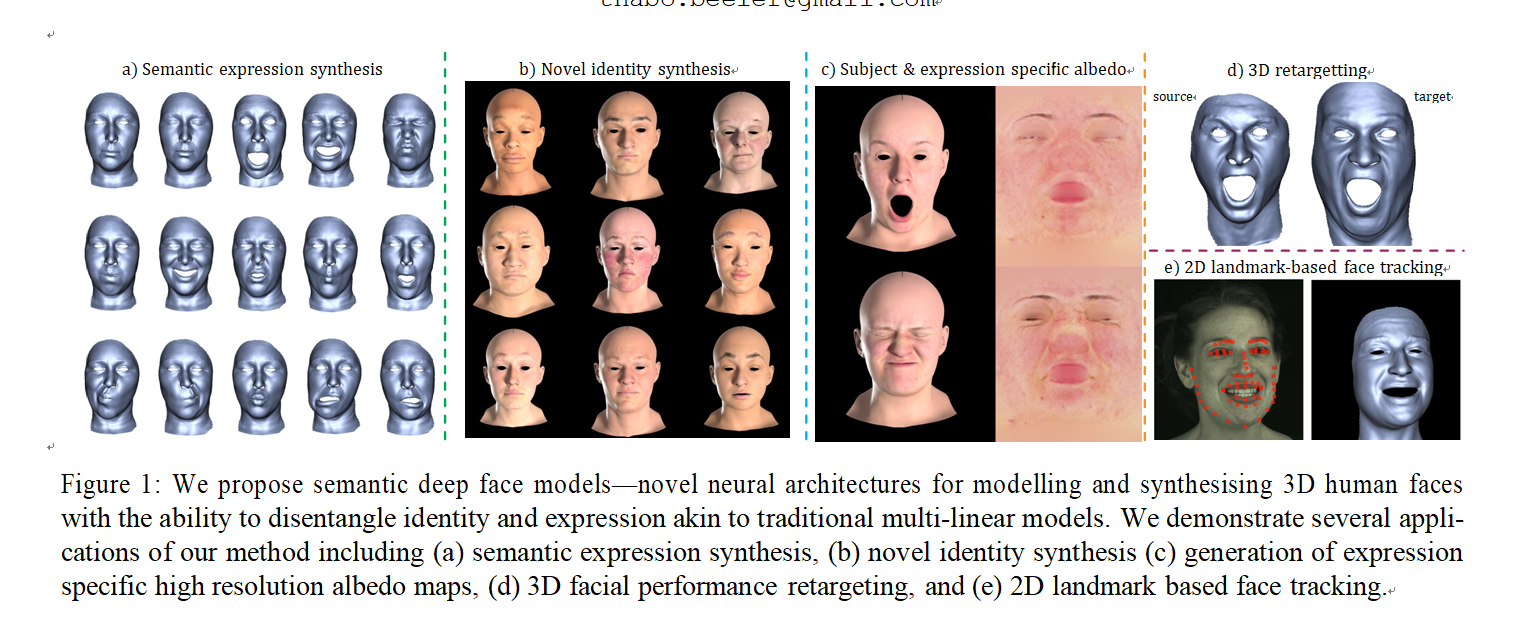
We demonstrate the value of our semantic deep face model with several applications. The first is 3D face synthesis (see Section 4.2), where our method can generate a novel human face (geometry and texture) and the corresponding (nonlinear) expressions - a valuable tool for example in cre- ating 3D characters in virtual environments. We also show that nonlinear 3D facial retargeting can be easily accomplished with our network, by swapping the identity latent code while keeping the per-frame expression codes fixed (see Section 4.3). Another application of our model is 3D face capture and retargeting from video sequences, by regressing to our expression latent space from 2D facial landmarks (see Section 4.3.2). Finally, in our supplementary video we demonstrate how our method allows an artist to edit a performance, e.g. add a smile/frown to certain keyframes of a captured facial performance. To summarize, we present a method for nonlinear 3D face modeling including both geometry and appearance, which allows semantic control by separating identity and expression in its latent space, while keeping them coupled in the decoded geometry space.
2.Related Work
Facial blendshapes [23] have been conventionally used as a standard tool by artists to navigate the space of the geometry of human faces. In addition to being human interpretable, blendshapes are extremely fast to evaluate, and enable artists to interactively sculpt a desired face. Blanz and Vetter [7] proposed a 3D morphable model of human faces, by using principal component analysis (PCA) to describe the variation in facial geometry and texture. Similarly, Vlasic et al. [33] proposed a multi-linear model based on tensor decomposition as a means of compressing a collection of facial identities in various expressions. However, in both morphable models and multi-linear tensors, the orthogonality comes at the cost of losing interpretability. In addition to linear global models, multi-scale approaches have been developed [27][15], [9], with a focus on capturing and reconstructing local details and deformations. Building on top of the techniques mentioned above, several statistical models of the human face have also been built [13], [25], [8]. We refer to a comprehensive survey [10] of methods used in the statistical modelling of human faces.
Moving on to nonlinear geometry modelling, Tan et al.[31] proposed the use of a variational autoencoder (VAE)[22] to effectively compress and represent several categories of 3D shapes. They do so by describing the deformation of meshes in a local coordinate frame [26] and later reconstructing the positions of the mesh through a separate linear solve. In the context of human faces, Ranjan et al. [28] proposed the use of convolutional mesh autoencoders and graph convolutions as a means of expanding the expressiveness of face models. While they were able to achieve better reconstruction than linear models, disentangling facial iden- tity and expression was not one of their objectives. Recent works [20, 2, 16, 14, 1] have begun to explore the disentanglement of facial identity and expression inside a neural network. The state of the art performance of these methods on standard datasets [13, 25] indicate the benefit of learning disentangled representations with neural networks. However, these methods learn to disentangle latent identity and expression, while the disentanglement is factored by design into our architecture and is therefore more explicit. Addi- tionally work such as [20, 2, 14, 1] do not jointly model facial geometry and appearance, while we do.
The more recent work of Li et. al [24] is closest in spirit to our work. Though our methods seem similar at the onset, there are a few important differences. The first is that though we decouple identity and expression in the network’s latent space, our joint decoder can model identity specific expression deformations which [24] can not. Second, as we describe in Section 3.2, the manner in which we use dynamic facial performances for training readily makes our method applicable to retarget and reconstruct performance from videos, and addresses another limitation of [24]. Another interesting contribution in neural semantic face modelling is the work of Bailey et. al [3], where semantic control over expression is achieved through rig parameters instead of blendweights. However, since their method is rig specific, and doesn’t model appearance, it unfortunately cannot be used for several of the applications demonstrated in this work.
In this work, we extend the state of the art in non-linear semantic face models, by proposing a novel neural architecture that explicitly disentangles facial identity and expression in its latent space, while retaining identity-expression correlation in geometry and appearance space. Through the use of blendweights, our method provides intuitive control over the generated expressions, retaining the benefits of tra- ditional multi-linear models, with increased expressiveness, and lends itself to applications in 3D face synthesis, 2D and 3D retargeting, and performance manipulation.
3. Methodology
We now present our method, starting with an overview (Section 3.1), our data acquisition and processing steps (Section 3.2), a description of the main architecture for se- mantically generating face geometry and low resolution ap- pearance (Section 3.3), our appearance super-resolution ap- proach (Section 3.4), and details on training (Section 3.5).
3.1.Concept Overview
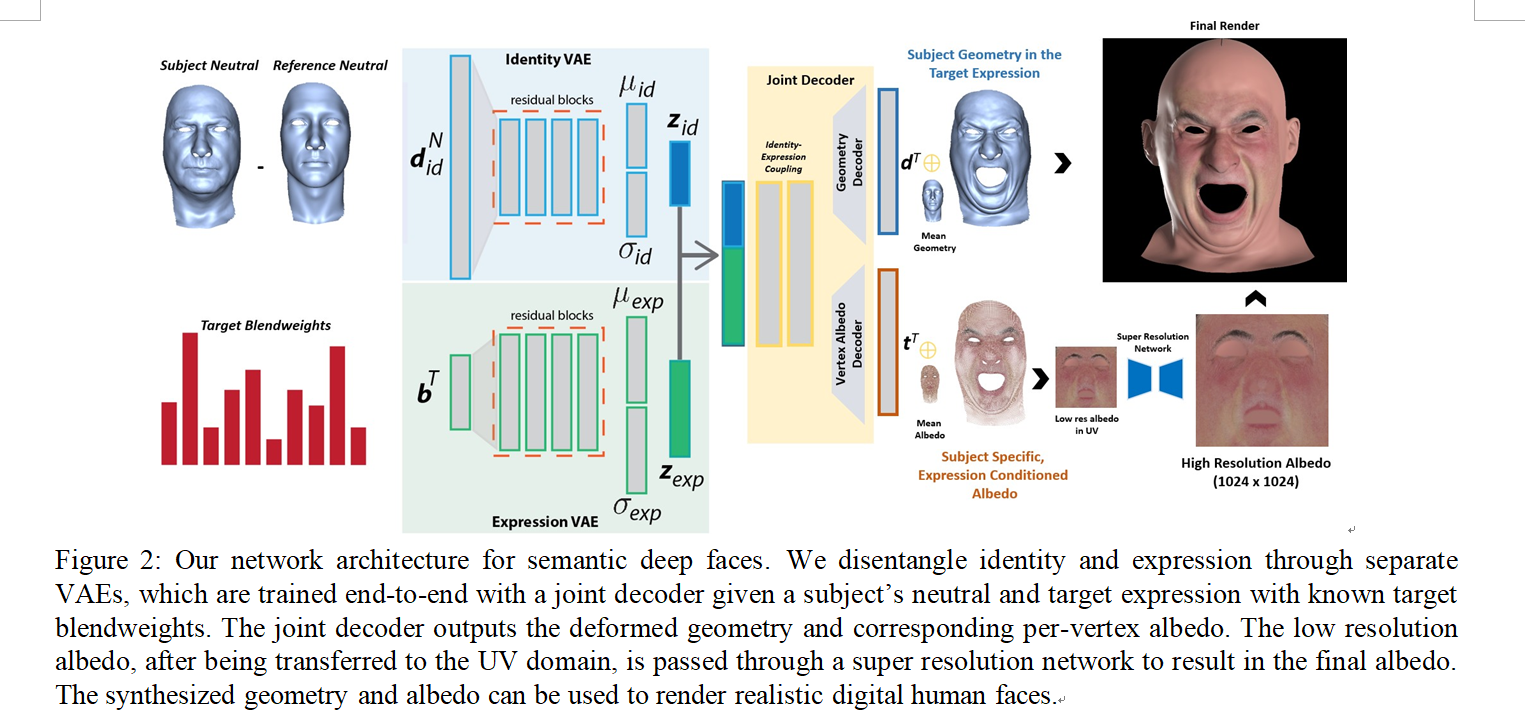
In this work, we assume that we are given access to a 3D face database consisting of several subjects in a fixed set of expressions, where the meshes are assumed to be in full vertex correspondence, similar to the datasets that tra- ditional face models are built from. Our method can op- tionally also take appearance data in the form of per-vertex color information, corresponding to each expression. In ad- dition to the static expressions, access to registered dynamic performances of subjects can also be used whenever avail- able (although dynamic data is not mandatory). We address how such a database can be built in Section 3.2. We propose a novel neural approach to human face modelling consisting of a pair of two variational auto-encoders (VAE), which use such a database to build a latent space where facial identity and expression are guaranteed to be disentangled by design, while at the same time allowing a user to navigate this la- tent space with interpretable blendweights corresponding to semantic expressions.
Given the neutral geometry and albedo of a subject, and a target blendweight vector, our collection of networks learn to deform the subject’s neutral into the desired captured expression, and also generate the corresponding per-vertex albedo. In the process of doing so, an identity VAE projects the subject’s face onto a latent space of facial identities while an expression VAE projects the target blendweight vector into a latent expression space. By combining the information from the identity and expression embeddings, a joint decoder learns the nonlinearity of facial deforma- tion to produce per-vertex displacements that deform the given neutral into the desired expression, along with non- linear albedo displacements that represent a corresponding expression-specific albedo. Our VAE learns the high-level correlation between the facial geometry and albedo. The per-vertex albedos are sampled as texture images in the UV domain at relatively low resolution, and are then upsampled with a variant of the Pix2PixHD architecture [34] in order to generate a high-resolution detailed facial textures.
3.2.Data Acquisition and Processing
Before we describe our algorithm in detail, a funda- mental requirement of our method is a registered 3D face database of different subjects performing a variety of fa- cial expressions. Since most existing 3D databases of hu- man faces [25, 13, 8] are limited in their geometric resolu- tion, and lack either variations in the identities of subjects [25, 13] or do not contain sufficient examples of the same subject performing different expressions, we capture and build our own 3D facial database. In a passively lit, multi- camera setup, we capture 224 subjects of different ethnici- ties, genders, age groups, and BMI. Subjects were carefully chosen such that each of the sampled distributions are as uniformly represented as practically possible. Each of the 224 subjects was captured performing a pre-defined set of 24 facial expressions, including the neutral expression. In addition to capturing the static expressions of 224 subjects, we also captured a dynamic speech sequence and a facial workout sequence for a subset of 17 subjects. The cap- tured images of subjects in various expressions were recon- structed using the method of Beeler et. al [4]. A template mesh consisting of 49,000 vertices was semi-automatically registered to the reconstructions of each subject individu- ally, and a 1024x1024 albedo texture map was generated by dividing out the diffuse shading given a measured light probe. As a result of this, we end up with a total of 5,376 meshes and textures (224 subjects x 24 expressions) that are in full correspondence with one another. We further stabi- lize the expression to remove any rigid head motion [5] and align all of them to the same canonical space. For training the albedo model, we sample the per-vertex albedo color and store the RGB information with each vertex, form- ing a 6-dimensional vector (XYZRGB). For the subjects for whom dynamic performances were captured, we start from their registered static meshes and build a subject spe- cific anatomical local face model [35]. This subject spe- cific model is then used to track the dynamic performance of the subject. For the 17 subjects we recorded, we recon- structed and tracked a total of 7,300 frames. Next, we as- sociate blendweight vectors to each registered mesh. For the static shapes, since each mesh corresponds to a unique, pre-defined expression, the blendweight vectors are one- hot encoded vectors corresponding to the captured expres- sion. This results in the assignment of a 24 dimensional
blendweight vector b 24 to each shape. However, the
assignment of blendweight vectors for a dynamic shape is
not straightforward as the subject may have performed an expression that could only be explained by a combination of the individual shapes. Therefore, we fit a weighted com- bination of the 24 registered shapes of the subject in a least squares sense to the tracked performance. This gives us op- timal blendweights for each frame in the performance. As we will show later (Fig. 5 (c)), the linear blendshape fit is only a crude approximation of the real shape. We there- fore discard the linear shape estimate (keeping only the opti- mized blend weights) and use the captured shape as ground truth to train our decoder. This way, we can leverage both static and dynamic data for training. A conceptual overview of our architecture is shown in Fig. 2.
3.3. A Variational Multi-Nonlinear Face Model
From the database described in Section 3.2, we com- pute the mean of all subjects in the neutral expression and call this shape the reference mesh R. We then subtract R from the original shapes, providing us with per-vertex dis- placements for each identity in the neutral expression. We identically pre-process the per-vertex albedo by subtracting the mean from each of the training samples. We will de- scribe the model now in the context of one subject, where subscripts id and exp represent the identity and expression components of the subject, respectively, and superscripts N and T correspond specifically to neutral and target expres- sion shapes.
The mean-subtracted neutral displacements dN are fed as the input to an identity VAE. We use displacements rather
than other representations like the linear rotation invariant (LRI) coordinates [26] as used by Tan et. al [31] since our input shapes are carefully rigidly stabilized. Our iden- tity encoder Eid is a fully connected network consisting of residual blocks that compress the input displacements into a mean µid and standard deviation σid.
µid, σid ← Eid(dN ). (1) At training time, the predicted mean and standard devi- ation vectors are used to sample from a normal distribution
using the re-parametrization method of Kingma et. al. [22] to produce a nid-dimensional identity code zid.
zid ∼ N (µid, σid).
The output of each fully connected layer except the ones predicting the mean and the standard deviation are activated with a leaky ReLU function. The identity encoder only ever sees the displacements of different subjects in the neutral expression, crucial for the decoder to explicitly decouple identity and expression.
In parallel, a second expression VAE, Eexp, takes a blendweight vector bT corresponding to target expression T as its input and compresses or expands it into a variational latent space zexp of nexp dimensions. Similar to the identity encoder, the expression VAE is also a fully connected net-
work with residual blocks and leaky ReLU activations. The expression VAE also outputs a mean and standard deviation vector that are fused into the expression code zexp.
µexp, σexp ← Eexp(bT ) (3)
zexp ∼ N (µexp, σexp). (4)
Our choice to use blendweights to condition the decoder is motivated by two reasons. The first is that blendweights provide a semantic point of entry into the network and can therefore be manipulated at test time by an artist. Second, one of our objectives is to force the network to disentangle the notion of facial identity and expression. Blendweights are a meaningful representation to learn this disentangle- ment as they contain no notion of identity and are purely de- scriptive of expression. The identity and expression codes are concatenated into a vector of dimension nid + nexp and fed to a decoder D that learns to correlate the identity and expression spaces and eventually reconstructs the given identity in the desired expression with corresponding per- vertex albedo estimate. The decoder is a fully connected
network that outputs vertex displacements dT with respect to the reference mesh R, and albedo displacements tT as
[dT , tT ] ← D(zid, zexp). (5)
Disentanglement by Design The joint decoder takes the two variational codes produced independently by the two VAEs to reconstruct the input subject in the desired ex- pression. Since the two latent codes are fully disentangled, the decoder must learn to correlate identity and expression codes to reconstruct the training shapes. This combina- tion of a disentangled latent space and correlated geometry space enables to capture identity specific deformations (in both shape and albedo) for the same semantic expression, as shown in Fig. 3.
We use four residual layers in both Eid and Eexp, where the dimensions of the layers are fixed to nid and nexp, respectively. Following our experiments outlined in Sec- tion 4, we set nid = 32 and nexp = 256 for all results. We resorted to the use of a VAE as opposed to a generative model to avoid running into mode collapses and to compen- sate for the lack of extensive training data. Our disentangle- ment framework is otherwise generic and could readily ben- efit from the use of graph convolutions [28] and other neu- ral concepts that focus on reconstruction accuracy. In other words, the novelty of our method primarily stems from our ability to semantically control a powerful nonlinear network while ensuring that it’s internal representations fully disen- tangle facial identity and expression.
3.4. Appearance Super-Resolution
The predicted per-vertex albedo displacements tT are added to the mean albedo and transferred to the UV do-
main. As seen in Fig. 2, the resulting texture map contains coarse information, such as the global structure of the face (the position of the eyes, mouth etc.), expression dependent effects (blood flow), as well as identity cues (ethnicity, gen- der etc.). What is missing are the fine details that contribute to the photo-realistic appearance of the original high reso- lution albedo. Our goal is to regenerate these missing de- tails conditioned by the low resolution albedo, upscaled to the target resolution. We reformulate this super-resolution task as a residual image-to-image translation problem [19], trained on the captured high resolution albedo texture maps. The low resolution albedo is upscaled using bilinear inter- polation to the target resolution (1024 x 1024). The up- scaled albedo AUp is then fed to a generator GRes [34] that outputs a residual image ARes, which is combined with with AUp to produce the final texture A . The discrimina- tors that provide adversarial supervision to the generator are multiple Markovian patch-based discriminators Dp, each of which operates at a different scale p of the input. We do not use any normalization layers in both the generator and the discriminators.
3.5. Training
Geometry VAEs: The identity and expression VAEs, along with the joint decoder, are trained end-to-end in a fully supervised manner using both static and dynamic per- formances. We penalize the reconstructed geometry with a L1 loss, and the identity and expression latent spaces are constrained using the KL divergence. Training takes around 4 hours on single Nvidia 1080 Ti GPU. We initialize both encoders and the decoder following Glorot et. al [17], and use the ADAM optimizer [21] with a learning rate of 5e-4.
Albedo Super-Resolution: The residual generator GRes is trained akin to the generator in [34], using both ground truth and adversarial supervision. For ground truth supervi- sion with the captured high resolution albedo AGT , we use
an L1 loss (L1) and the VGG-19 [30] perceptual loss LV GG.
We train each discriminator Dp using the WGAN-GP loss
as proposed by Gulrajani et. al [18]. We use a learning rate of 1e-4 and optimize the generator and discriminators using the ADAM optimizer [21]. We refer to our supplementary material for additional details on the network architecture and loss formulations.
4. Results and Discussion
Our goal is to produce a semantically controllable, non- linear, parametric face model. In this section we inspect the disentangled latent spaces for identity and expression, and show how the nonlinear representation is more power- ful than traditional (multi-)linear models, while providing the same semantic control
4.1. Quantitative Evaluation on Facewarehouse
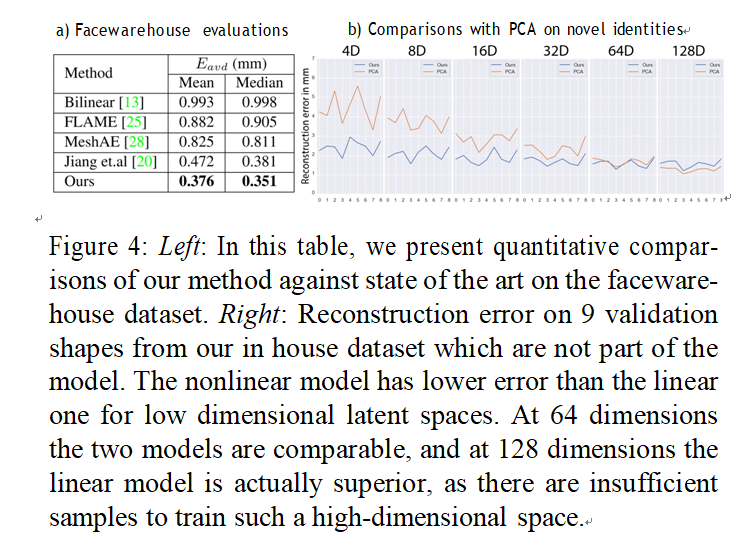
The Facewarehouse dataset [13] contains meshes of 150 identities in 47 different expressions, where each mesh con- tains 11,518 vertices. Since the meshes in Facewarehouse do not have an associated texture map, we train only the geometry decoder (Fig. 2) for this experiment. Similar to Jiang et. al [20], we train our model on an augmented set of the first 140 identities and their expressions, and test on the 10 remaining identities.
The table in Fig. 4 (left) compares our reconstruction ac- curacy on the Facewarehouse dataset to existing state of the art in 3D face modelling. To enable a fair comparison to existing work, we also fix the total dimensionality of our latent spaces to 75 dimensions like other works. See the supplementary material for qualitative results on the Face- warehouse dataset.
4.2. Disentangled Latent Spaces
Our disentangled representation allows for smooth con- trol over both identity and expression independently.
4.2.1 Identity Latent Space
Varying the identity code while keeping the expression code fixed will produce different identities with the same expres- sion. Fig. 3 (a) (top 2 rows) shows the result of random samples drawn from the identity latent space, also rendered with the resulting upsampled albedo. The choice of a vari- ational autoencoder to represent the identity space allows to smoothly morph between different subjects by (linearly) interpolating their identity codes. As Fig. 3 (b) shows, the degree of nonlinearity reflected in the output shapes varies as a function of the dimensionality of the latent space, where a lower dimensionality will force higher nonlinearity. No- tice how interpolating between two identities appears to pass through other identities for lower dimensional identity spaces. While a lower dimensional latent space reduces the reconstruction accuracy (see Fig. 4) due to the higher com- pression, our representational power is still significantly higher than a linear model (PCA). Increasing dimensions diminishes this advantage due to the relatively low number of training samples.
4.2.2 Expression Latent Space
While it would be an option to directly sample the expres- sion latent space analogous to the identity latent space, this would not allow for semantically meaningful control. For human animators it is critical to provide an intuitive con- trol structure to animate the face, referred to as rig. The most well-known rigging concept for facial animation are blendshapes, which are extremely intuitive as they allow the animator to dial in a certain amount of a given expression. These can then be superimposed to provide the final shape. In our system, the exposed expression controls are provided in exactly the same way, via a vector of blendweights that encode the intensity of the individual shapes to be dialed in. Due to the disentangled nature of identity and expres- sion spaces, it is possible to synthesize any desired expres- sion as shown in the bottom part of Fig. 3 (a) for a given identity. Here we provide one-hot blendweight vectors to the network and generate the complete set of blendshapes. As such, the proposed model can be readily adopted by animators. Corresponding high resolution albedo textures for the synthesized expressions are also produced by our method, as illustrated in the expression interpolation exam- ple in Fig. 3 (c). In addition to providing an interface akin to blendshapes, our method has quite some advantages over a linear blendshape basis. Fig. 5 (a) shows that our model is much more robust when extrapolating along an expres- sion dimension beyond [0,1], unlike the linear model, which leads to exaggerated and unusable shapes, especially to- wards the negative direction. Furthermore, linearly varying the weight within [0,1] provides a nonlinear effect on the generated shape, as demonstrated on the smile expression, where the generated smile starts off as a closed mouth smile up until 0.6, and then opens up, which feels more natu- ral than the monotonous interpolation of the linear model. This nonlinearity is especially important when superimpos- ing expressions (Fig. 5 (b)). For a linear model, the latter only makes sense for a few combinations of expressions, and hence blendshape editing often yields undesired shapes quickly, especially for novice users, whereas the proposed method is more robust in such cases. As expected, our nonlinear model has higher expressive power than its lin- ear counterpart (Fig. 5 (c)) when fitting to a ground-truth reconstructed performance, the linear model incurs a larger reconstruction error for the same blend vector dimension- ality. Using the fitted linear blendweights as input to our network, our method achieves much lower errors, close to the optimal expression the model can produce, found in this case by optimizing in the expression latent space.
4.3.Facial Performance Retargeting
Our method also lends itself to facial performance trans- fer using blendweights or 2D landmarks.

4.3.1 Blendweight Retargeting
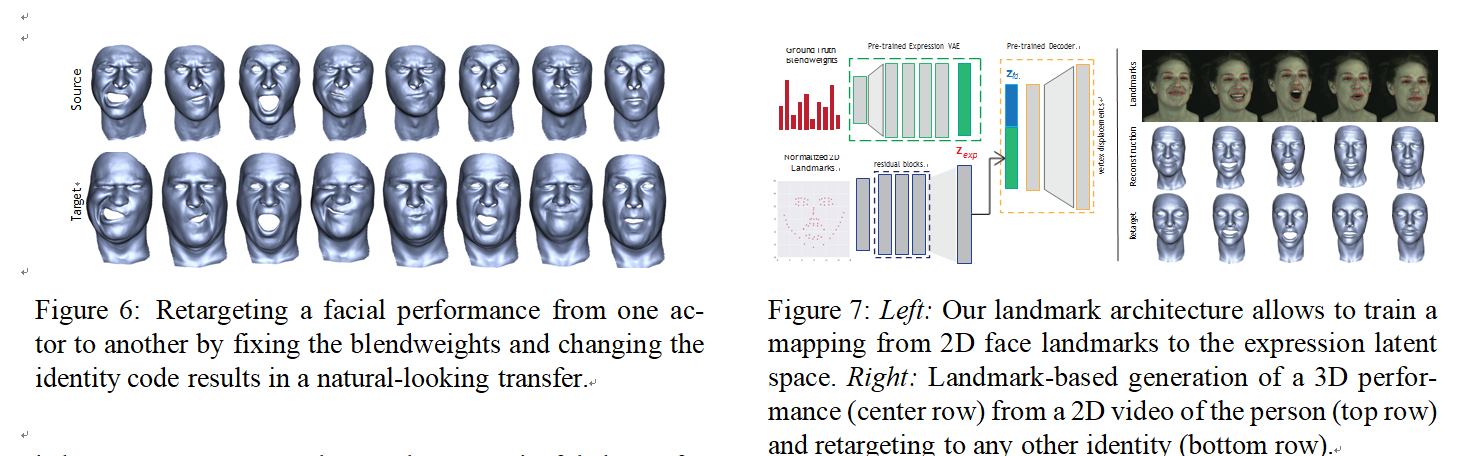
Retargeting performances by transferring the semantic blendweights from one character to another is a common approach in facial animation. The same paradigm can be used with our nonlinear face model, by first determining the identity code of the target actor using the identity VAE (given the target neutral expression), and then injecting the per-frame blendweights to the expression VAE. Fig. 6 il- lustrates this procedure, transferring the expression weights obtained from a performance onto a novel identity.
4.3.2 2D Landmark-Based Capture and Retargetting
Another interesting scenario is facial performance capture and retargeting based on 2D facial landmarks in videos. Here we show an extension of our architecture that allows an interface to the latent expression code via 2D landmarks. Given a subset of our facial database where frontal face im- agery is available, we detect a typical landmark set [11] and perform a normalization procedure to factor out im- age translation and scale (based on the inter-ocular dis- tance). The normalized landmarks are then stacked into a
vector, and fed to a network that aims to map the landmarks to the corresponding expression code zexp. We illustrate this landmark architecture in Fig. 7 (left). The network is
trained with ground truth blendweights which allows su- pervision on the expression code, given the pre-trained ex- pression VAE, and we include the resulting geometry in the loss function using the pre-trained decoder. The result is a means to generate expressions based on 2D landmarks, which allows further applications of our deep face model including landmark-based performance capture (Fig. 7 right
- center row) and retargeting to a new identity (bottom row).
4.4. Limitations and Future Work
While the proposed expression encoding is more robust to random blendweight combinations than linear models, it is however not guaranteed to produce meaningful shapes for any given blendweight vector. It would be very valuable to have a representation that maps the unit hypercube to the physically meaningful expression manifold in order to al- low random sampling that provides valid shapes spanning the complete expression space. Even though we incorpo- rate dynamic performances, we do not encode the tempo- ral information, which would allow to synthesize temporal behaviour, such as nonlinear transitioning between expres- sions. Lastly, we feel the proposed approach is not limited to faces but could provide value in other fields, for example general character rigging.
5. Conclusion
We propose semantic deep face models—novel neural architectures for 3D faces that separate facial identity and expression akin to traditional multi-linear models, but with added nonlinear expressiveness, and the ability to model identity specific deformations. We believe that our method for disentangling identity from expression provides a valu- able, semantically controllable, nonlinear, parametric face model that can be used in several applications in computer vision and computer graphics.
