부동소수점 (0.1 + 0.1 === 0.2??)

얼마전 퀴즈로 나왔던 부분을 정리한다.

컴퓨터에서 0.1 + 0.1 === 0.2라 입력하면 True일까? Flase일까?
정답은 False 이다.
(실제로 inspection에서 입력하면 true로 나온다.ㅎㅎ)

컴퓨터에서 숫자를 표현하는 방법은?

사람은 10진법으로 숫자를 표현하지만,
컴퓨터는 2진법으로 숫자를 표현한다.

즉, 1, 0으로 모든 것을 받아 들인다.

왜냐하면 컴퓨터는 전기 신호로 모든 데이터를 처리한다.
전기 신호가 on이면 1으로,
전기 신호가 off이면 0으로 표현한다.

소수점은 어떻게 표현할까?

10진법의 숫자를 2진법으로 표현할 때 가장 문제가 되는 부분이 실수이다.
실수, 즉 0.1, 2.1과 같은 소수점을 2진법으로 정확하게 나타낼 수가 없다.

• 263 => 100000111
• 0.3 => 0.01001100110011........ (무한 반복....)

즉, 2진수로 표현하지 못하는 소수는 가장 근사치의 값으로 저장이 된다.

소수점을 저장하기 위한 방법

고정 소수점

• 정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해 놓고,
  해당 비트 만큼만 사용해서 숫자를 표현하는 방식

예를 들어, 263.3이란 실수를 표현하는데 4byte(32bit)를 사용하고,
부호는 1bit, 정수는 16bit, 소수는 15bit를 사용하도록 약속한 시스템이 있다고 하자.

정수인 263을 2진법으로 바꿔서 16bit로 저장하고,
소수인 0.3을 2진법으로 바꿔서 15bit로 저장한다.

즉, 이런 시스템에서는 부호는 +이므로 0이 저장되고,
정수인 263은 16bit를 사용하므로, 0000000100000111이 저장되고,
소수인 0.3은 15bit를 사용하므로, 010011001100110으로 저장이 된다..

정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만, 정밀한 숫자는 표현이 어렵고,
소수를 표현하는 bit를 늘리면 정밀한 숫자를 표현할 수 있지만, 큰 숫자는 표현이 어렵다.

부동 소수점

• 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로,
  유효숫자를 나타내는 가수와 소수점의 위치를 풀이하는 지수로 나누어 표현한다.
• IEEE 754는 전기 전자 기술자 협회(IEEE)에서 개발한 컴퓨터에서 부동소수점을
  표현하는 가장 널리 쓰이는 표준이다.
  [출처][위키백과](https://ko.wikipedia.org/wiki/%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90)

−118.625(십진법)를 IEEE 754로 표현해 보자.

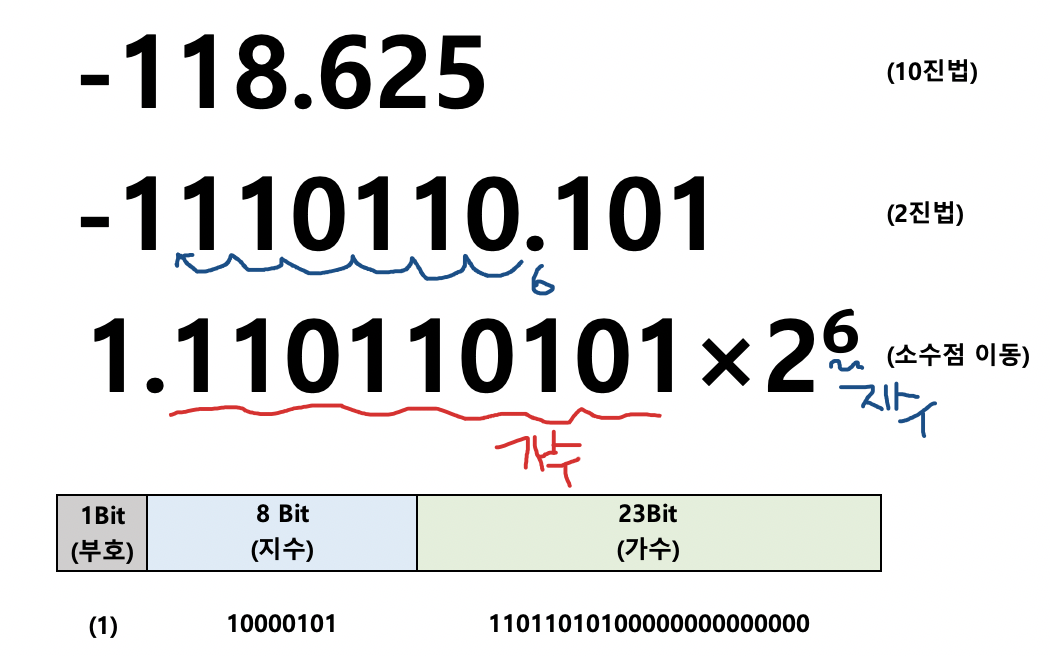
음수이므로, 부호부는 1이 된다.
그 다음 절대값인 118.625를 이진법으로 나타내면 1110110.101이 된다.
소수점을 왼쪽으로 이동시켜, 왼쪽에는 1만 남게 만든다.
즉, 1110110.101 = 1.110110101×2⁶ 과 같다.
이것을 정규화된 부동소수점 수라고 한다.

가수부는 소수점의 오른쪽이다. 부족한 비트 수 만큼 0으로 채운다.
결과는 11011010100000000000000이 된다.
지수는 6이므로, Bias를 더해야 한다. *
32비트 IEEE 754 형식에서 Bias는 127이므로 6+127 = 133이 된다.
이진법으로 변환하면 10000101이 된다.

Bias 표현법이라 127을 더하는건데, 자료를 봐도 이해가 안간다..ㅠㅠㅠㅠ
궁금하신 분들은 아래 링크 참고하세요
[참고][부동소수점에 대한 이해 - bias표현법](https://thrillfighter.tistory.com/349)

참고

• 컴퓨터는 어떻게 숫자를 세고, 문자로 표현할까
• 부동 소수점(Floating Point)란 무엇인가?
• 컴퓨터는 실수를 어떻게 이해할까? : 부동소수점
• 실수, 부동소수점