소수를 판별하는 알고리즘은 종종 알고리즘 문제에서 쓰입니다. 이 때 시간복잡도에 따라서 다르게 구현이 가능합니다.

1. 일반적인 소수 판별

소수는 자기자신과 1만을 약수로 가지는 수 이니깐, n미만의 숫자중에서 나머지연산을 했을 떄 0이되면 약수를 가지니깐 소수가 아닙니다.
이것을 코드로 옮기면 아래와 같이 됩니다.

Algorithm.java

import java.util.*;
import java.io.*;

public class Algorithm {

    static boolean isPrime(int n){ // 시간복잡도 O(N)
        if(n<2){
            return false; // 1은 소수가 아니기에 false
        }else{
            for(int i = 2; i < n; i++){
                if(n % i == 0) return false; // 나머지연산을 했을 때 0이 나오면 소수가 아니므로 false
            }
            return true; // 위의 case
        }
    }

    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine()); // 소수인지 판별할 숫자 input
        System.out.println( (isPrime(N) == true) ? "소수입니다" : "소수가 아닙니다.");
    }
}

위의 코드의 시간복잡도는 O(N)이며, N개의 수를 판별하면 O(N^2)이 됩니다.
시간이 상당히 오래걸리므로, 보통은 다음과 같은 방법을 씁니다.

2. 에라토스테네스의 체

에라토스테네스의 체는 많은 수의 소수판별을 할 때 유용합니다.
이 알고리즘의 원리는 해당수가 소수라면, 해당수의 배수들은 모두 해당수를 약수로 가지고 있으므로 소수가 되지 못합니다.

정리하자면,
1)지워지지 않는 가장 작은 수를 찾는다.(보통 2부터 시작)
2)해당 수는 소수이다.
3)해당수의 배수들을 모두 지운다.

예를 들어 설명하겠습니다.
N=100일때 1~100사이의 소수를 구해봅시다.
1은 예외이므로 제외하고 시작합니다.

먼저, 지워지지 않는 가장 작은수는 2이고, 2의 배수들을 다 삭제합니다.(검은글자는 소수거나 지워지지 않은 수, 회색글자는 지워진 수)

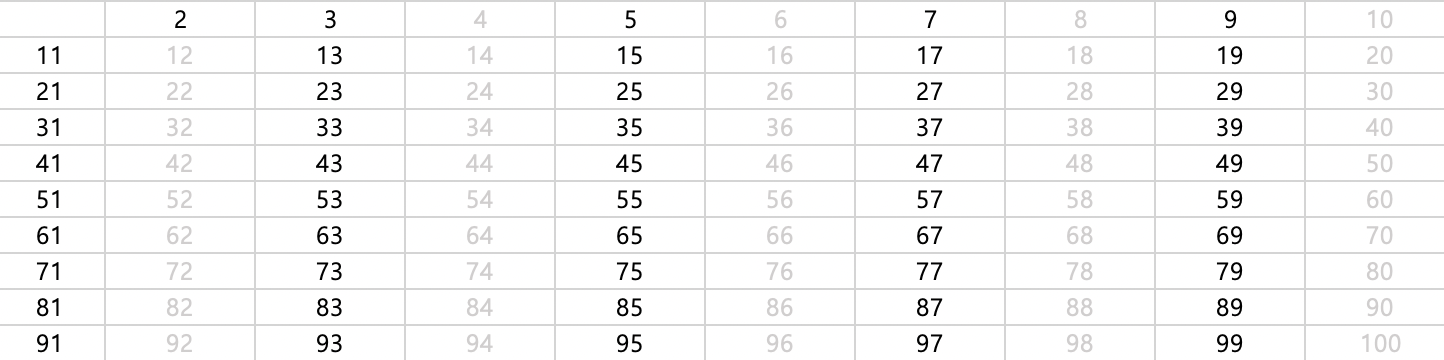
그 다음 지워지지 않는 가장 작은수는 3이고, 3의 배수들을 다 삭제합니다.

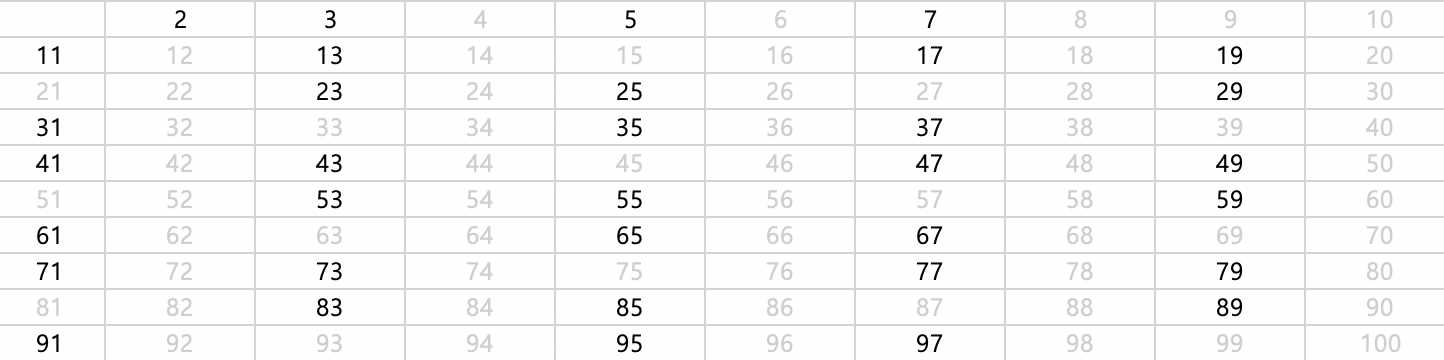
그 다음 지워지지 않는 가장 작은수는 5이고, 5의 배수들을 다 삭제합니다.

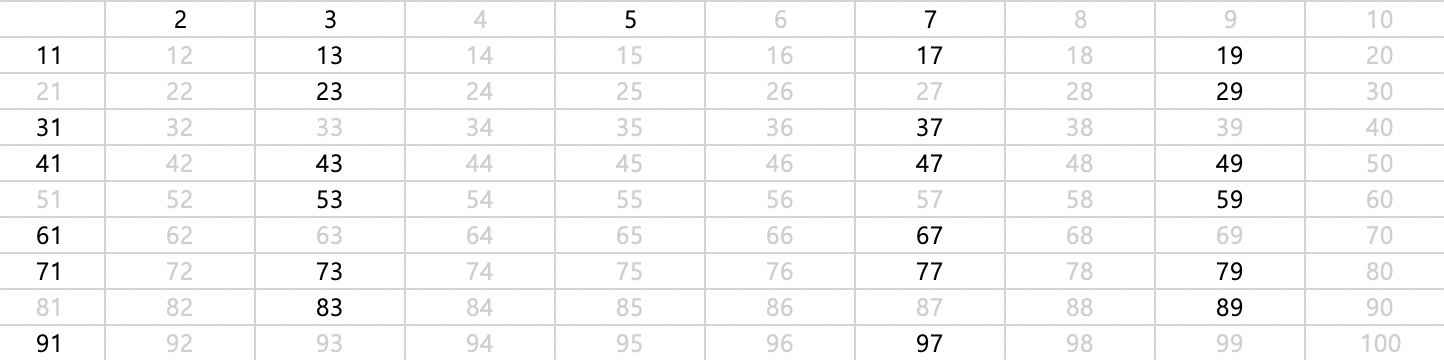
이 방식으로 하면 다음과 같이 됩니다.

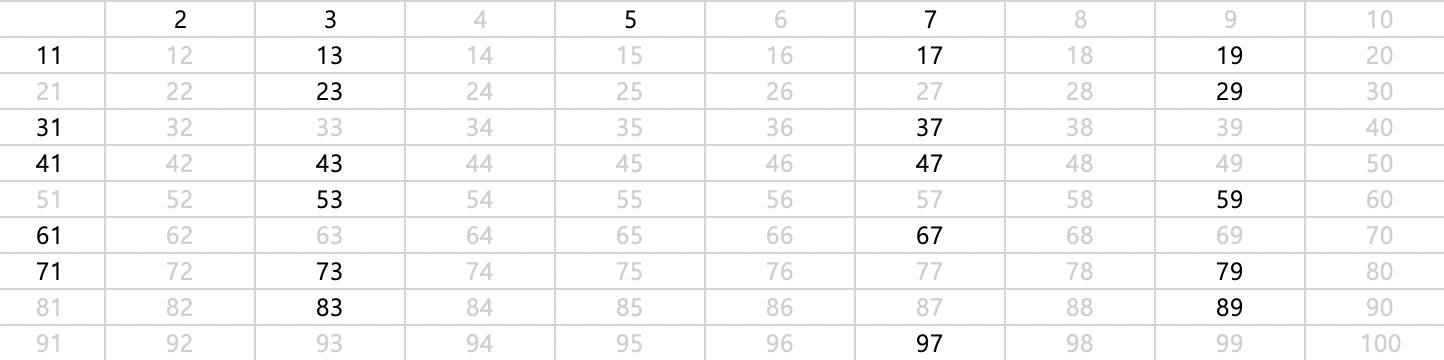
최종적으로 100 이하의 소수 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97이 나옵니다.

이러한 방법을 코드로 짜보면 다음과 같습니다.
Algorithm.java

import java.io.*;

public class Algorithm {

    static boolean[] isPrime;
    
    static void isPrime_fun(int n){ 
        isPrime = new boolean[n+1]; // N번째의 수 까지 받기위해 N+1까지 동적할당
        
        for(int i = 0; i < isPrime.length; i++){
            isPrime[i] = true; // boolean배열의 default값은 false이므로 true로 바꿔주기
        }
        
        isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아니니깐 false
        
        for(int i = 2; i <= Math.sqrt(n); i++){ // 2부터 n의 제곱근까지의 모든 수를 확인
            if(isPrime[i]){ // 해당수가 소수라면, 해당수를 제외한 배수들을 모두 false 처리하기
                for(int j = i*i; j<= n; j += i){//그 이하의 수는 모두 검사했으므로 i*i부터 시작
                    isPrime[j] = false;
                }
            }
        }
    } // isPrime_fun 함수 종료

    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine()); // 소수인지 판별할 숫자 input
        isPrime_fun(N);
    }
}

이와 같이 할시 시간복잡도는 O(n loglogn) 입니다.

연습문제

이제 연습문제로 다음을 출력해봅시다.
1부터 1000사이의 소수를 출력 후, 소수의 총 개수를 출력해봅시다.
output

2
3
5
7
11
13
// 중간 생략 ~~~~
983
991
997
소수의 개수 : 168