그래프와 순회

그래프 순회란 모든 정점을 방문하는 작업입니다.
그래프에서 노드끼리 간선으로 연결을 해준뒤, 방문을 하면 방문처리를 해 줘서 중복되지 않게 방문을 해야됩니다.

대표적으로 두 가지 방법이 있습니다.
1.깊이 우선 탐색(DFS)
2.너비 우선 탐색(BFS)

이 두가지의 방법은 아래와 같은 순서를 공통으로 가집니다.
1.시작점을 넣는다.
2.시작점과 연결되어있는 노드를 방문하고 출력과 방문처리를 해준다.
3.2번을 반복하여 방문할 수 있는곳은 모두 방문한다.

---

깊이 우선 탐색

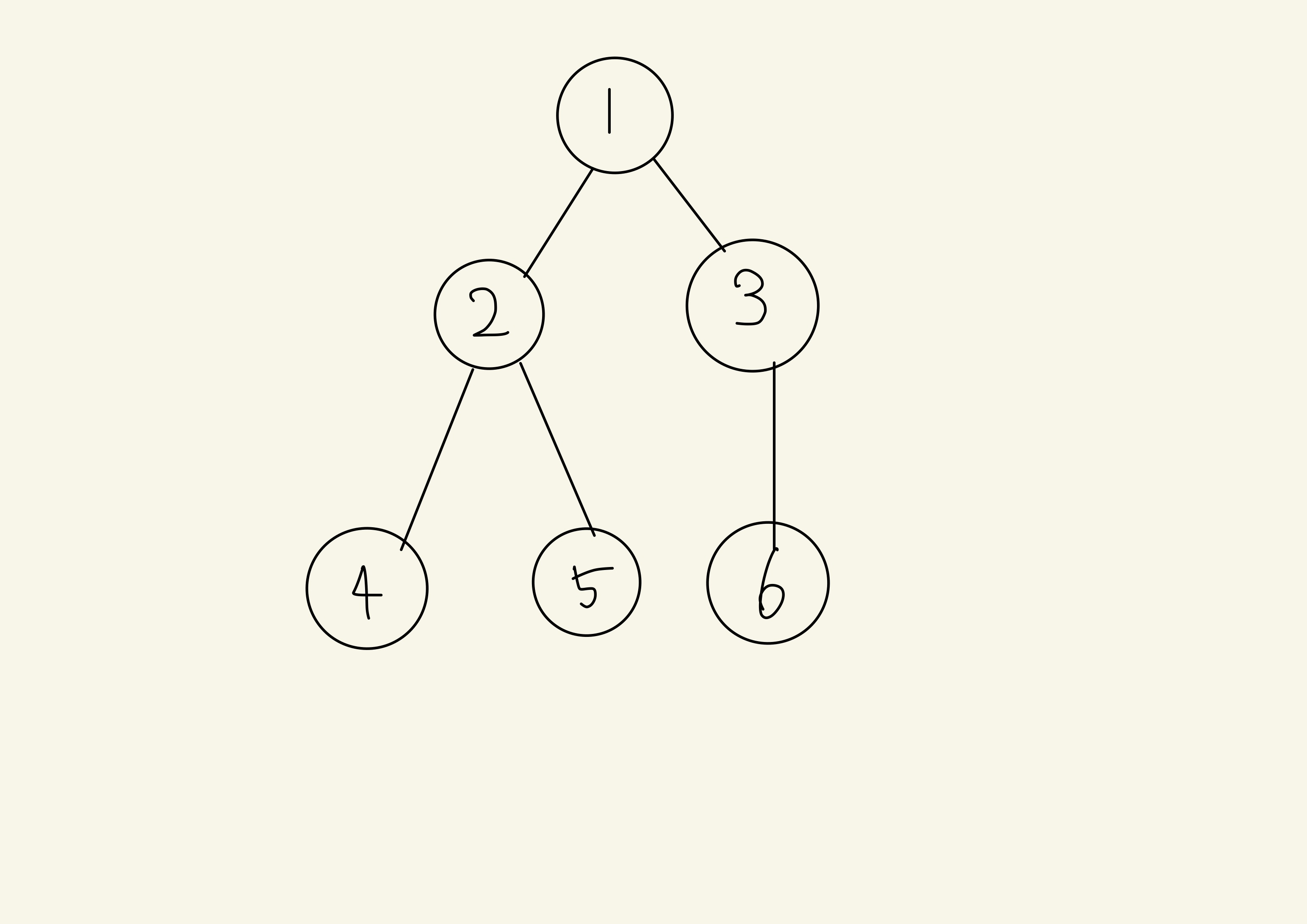
깊이 우선 탐색은 이름과 같이 깊이를 우선적으로 탐색을 하는 알고리즘입니다. 깊이 우선 탐색은 Stack과 재귀를 이용한 방법이 있는데 저는 재귀를 통해 보여드리겠습니다. 알고리즘의 순서는 다음 예시를 보겠습니다.
다음과 같은 Graph가 주어졌다고 가정하겠습니다.

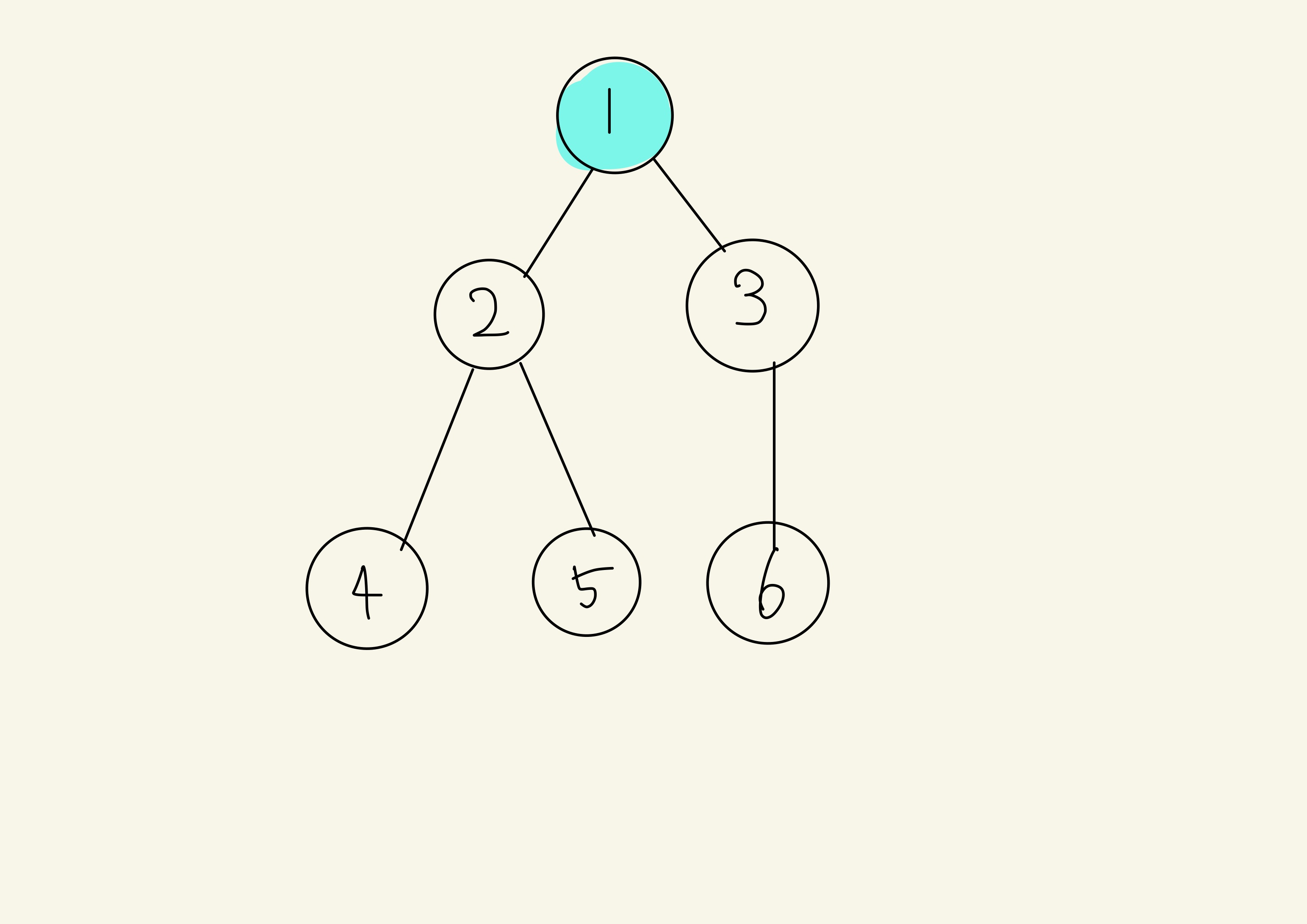
우선 시작지점인 1을 탐색합니다.

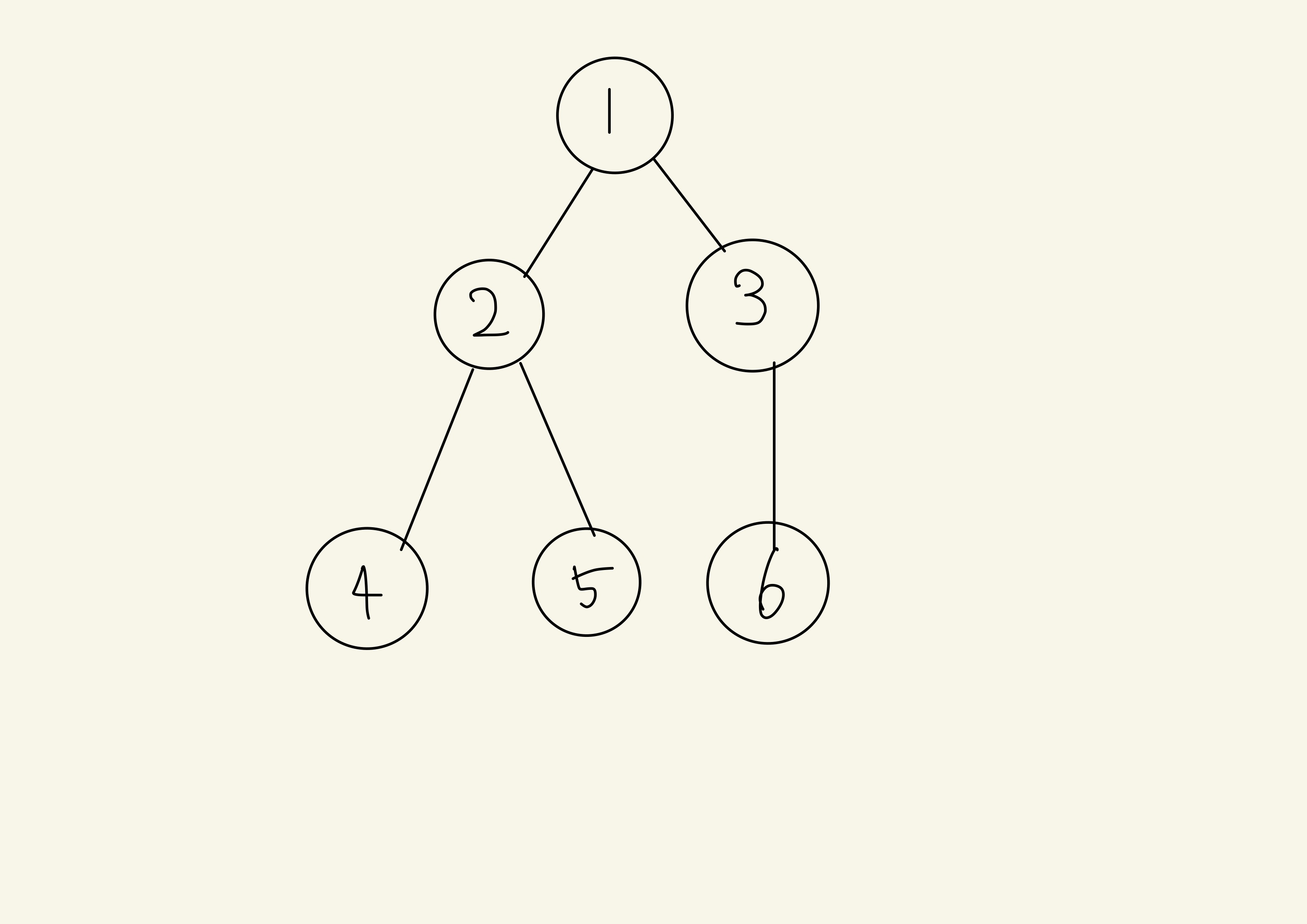
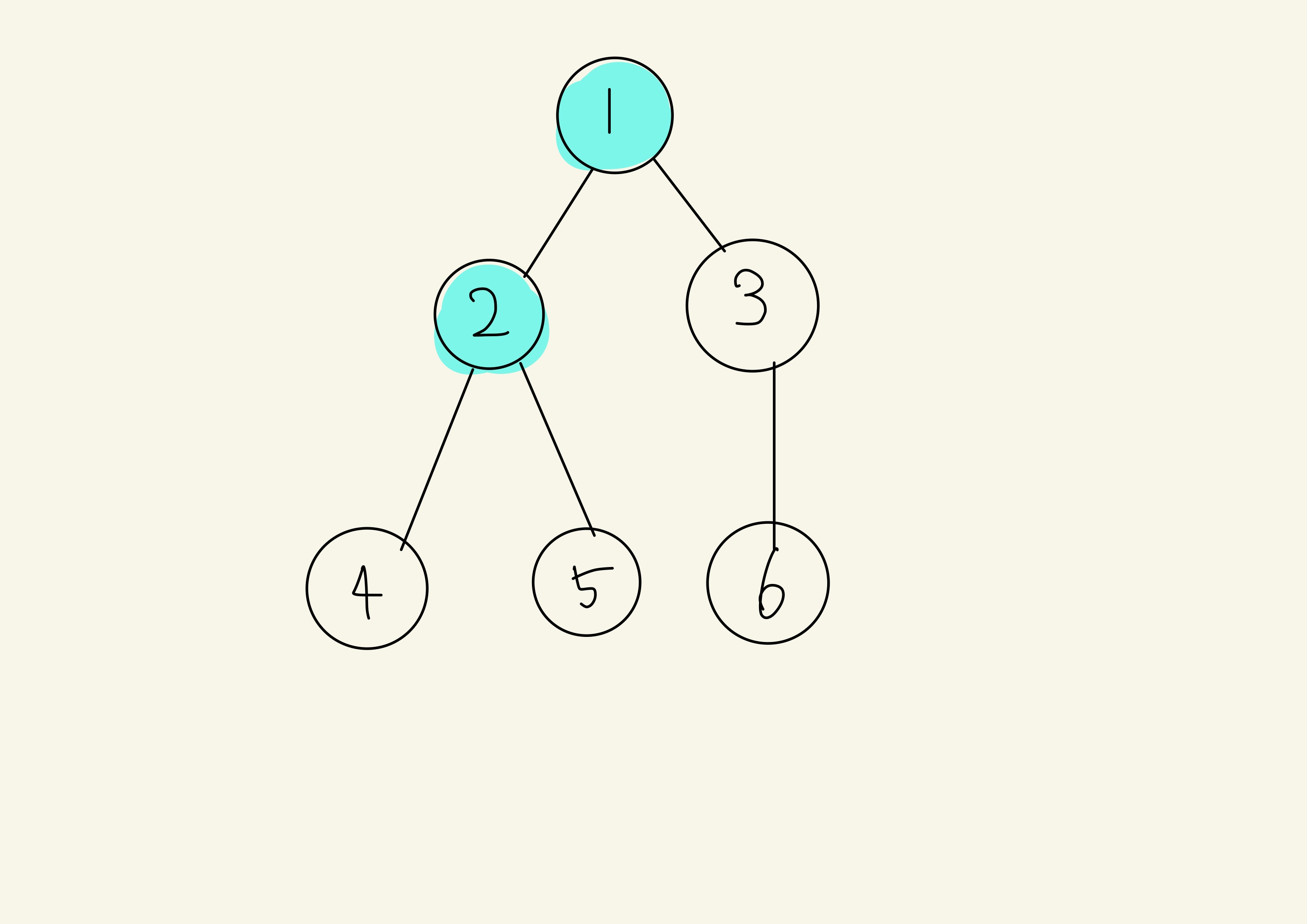
1을 방문했으니 방문처리를 해준 뒤, 1의 자식들을 살펴봅니다.
1의 자식은 2,3이 있는데 보통 알고리즘은 작은 수 -> 큰 수 순서로 짜서 2를 먼저 방문합니다. 3을 먼저 방문해도 상관은 없습니다.

2를 방문했으니 방문처리를 해준 뒤, 2의 자식을 살펴봅니다.
2의 자식은 4,5 있고 4를 방문처리를 먼저 해줍니다.

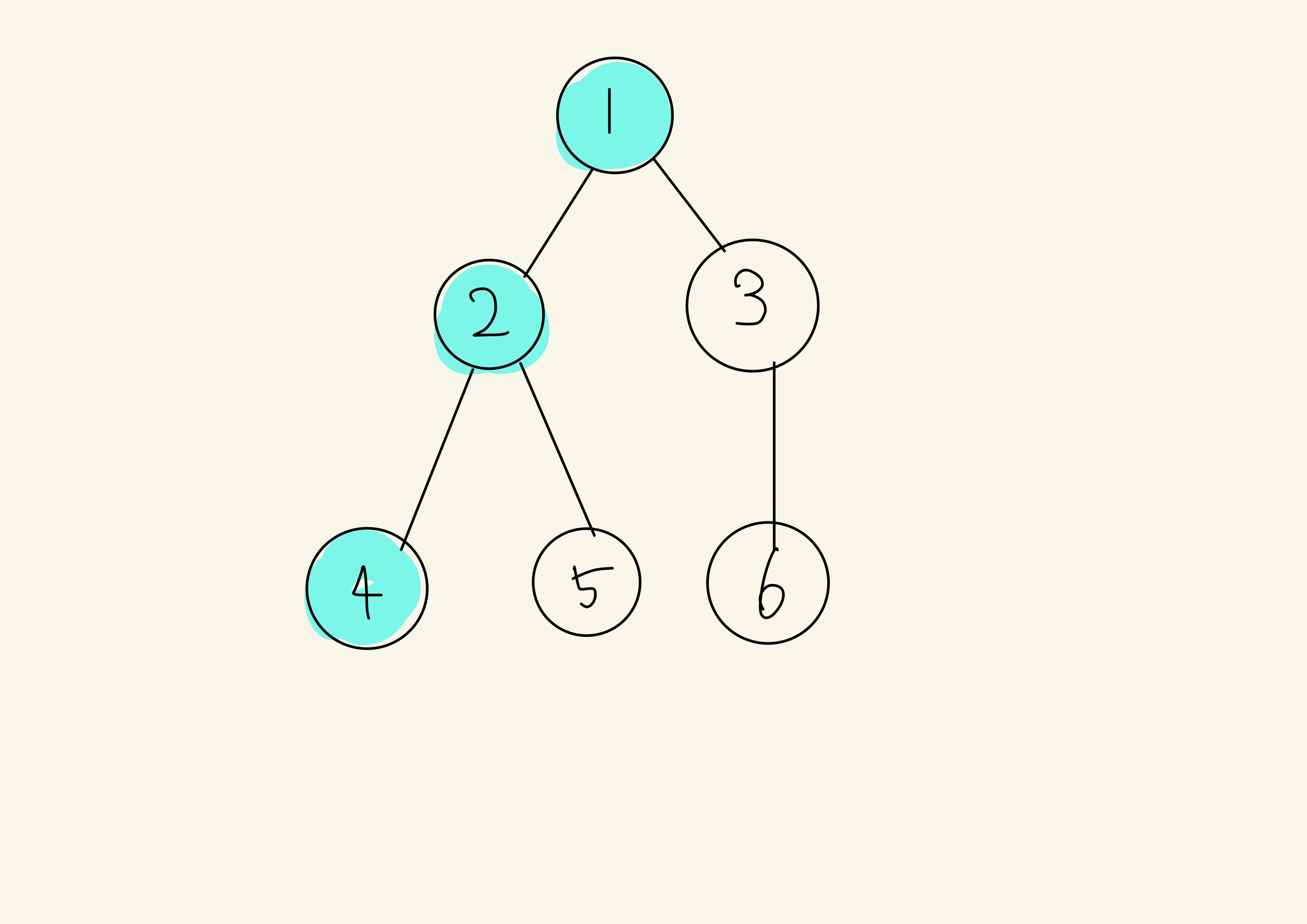
4를 방문했으니 방문처리를 해준 뒤 4의 자식이 없으니 다시 2로 돌아갑니다.
그리고 2의 자식중 5가 있으니깐 5를 방문해줍니다.

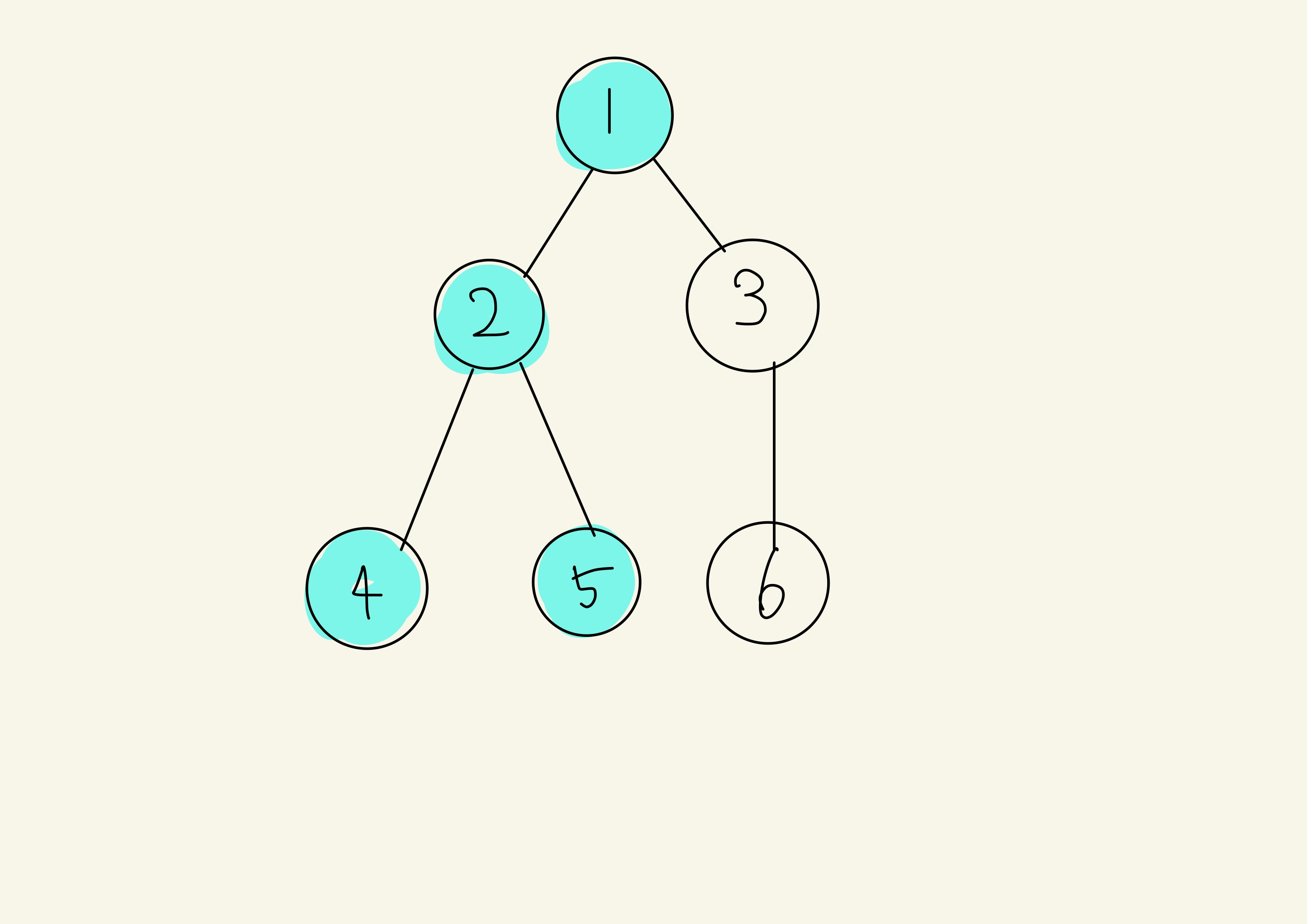
5를 방문했으니 방문처리를 해준 뒤, 자식이 없으니깐 다시 1로 돌아갑니다.
1의 자식중 방문을 하지 않은 자식이 3이 있으니깐 3을 방문해줍니다.

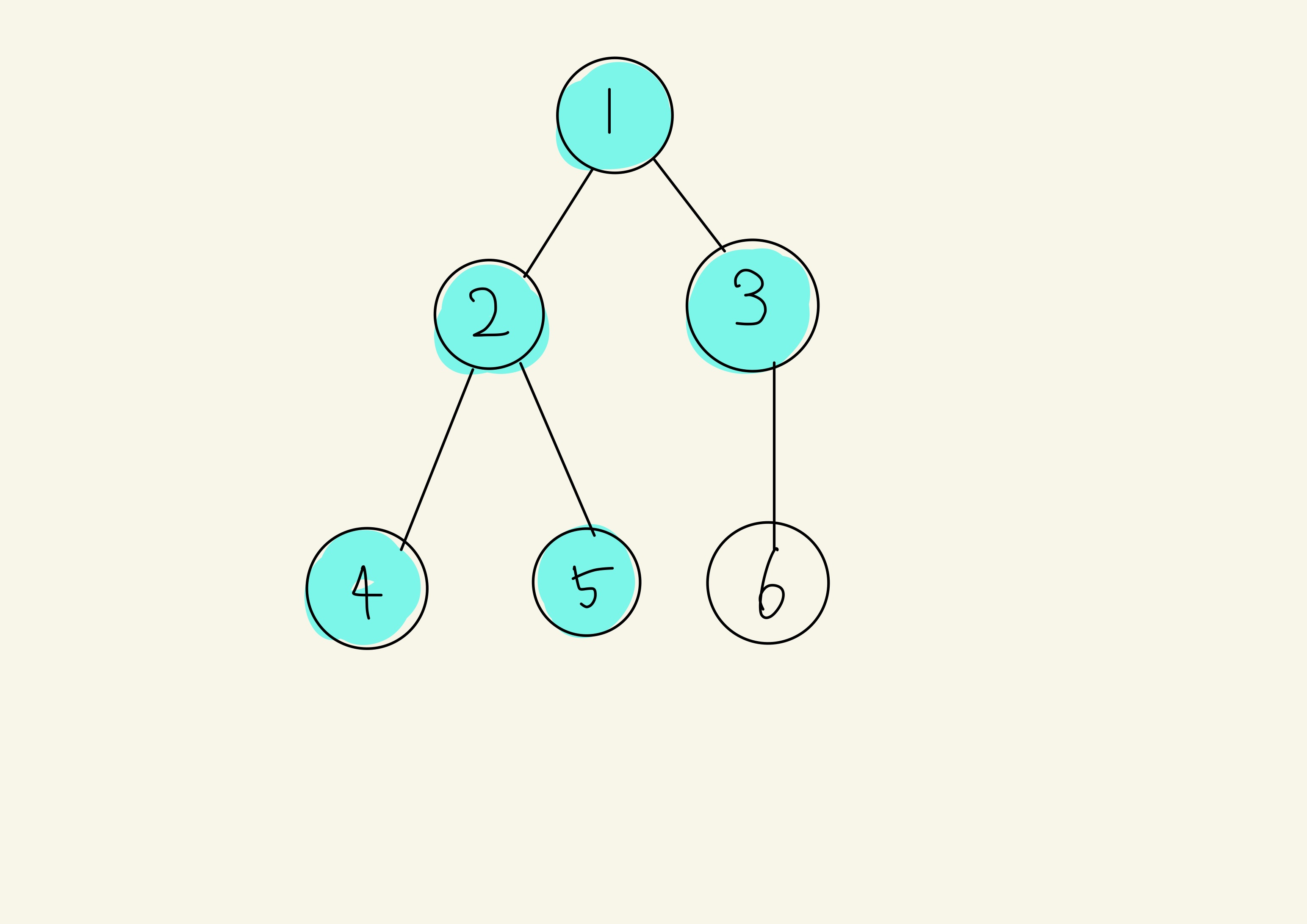
3을 방문처리 해준 뒤, 마지막으로 남은 자식 6을 방문해줍니다.

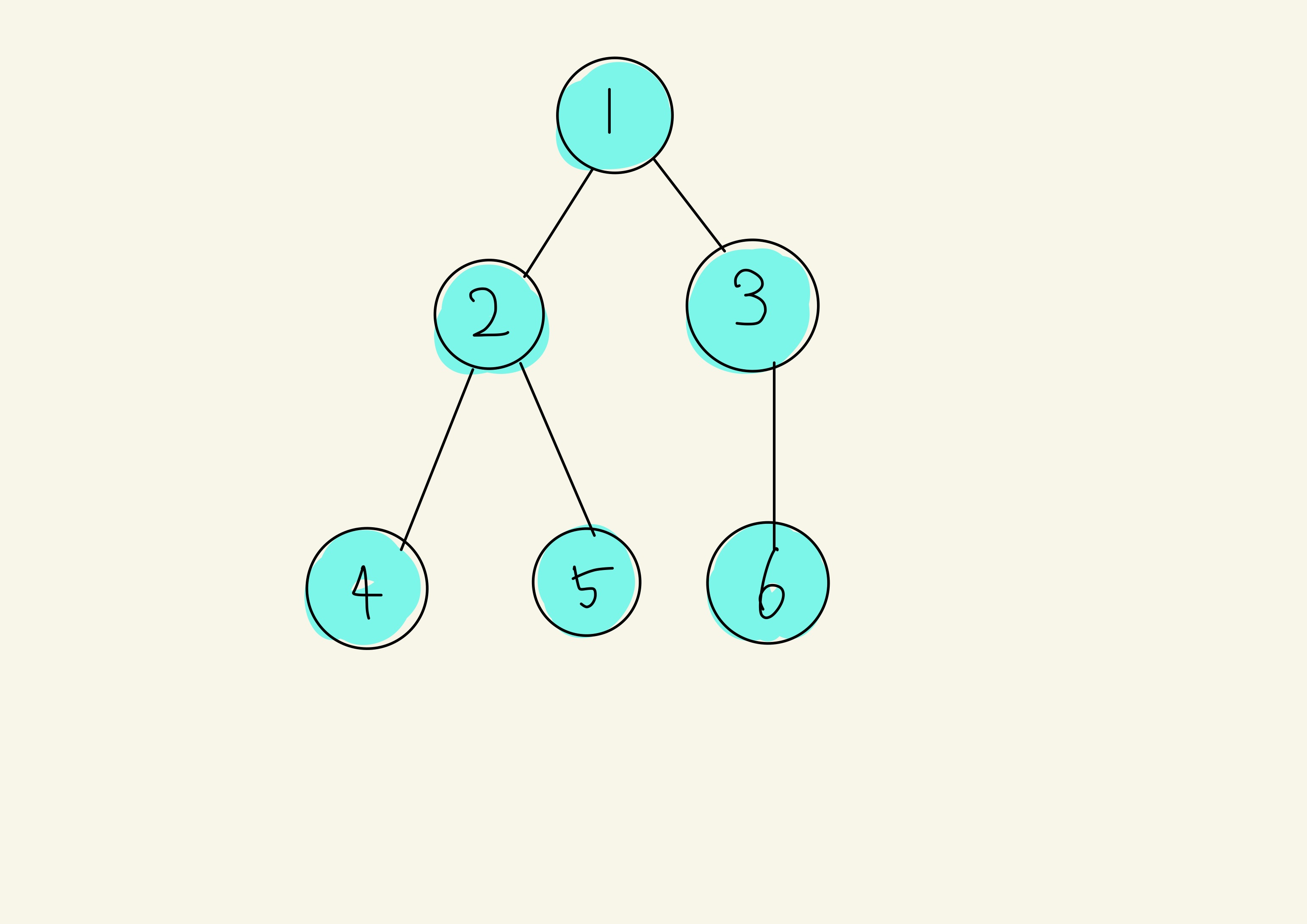
이렇게 하면 모든 노드를 탐색완료 했습니다.

이러한 과정을 코드로 나타내면 다음과 같습니다.
C++

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define endl '\n'
using namespace std;

vector<vector<bool> > v;
vector<bool> visited;
int n, m, start;

void dfs(int k){ // 깊이 우선 탐색
    visited[k] = true; // 방문처리
    cout << k << " "; // 방문한 노드 출력 
    for(int i = 1; i <= n; i++){ // 1번 노드부터 n번노드까지 연결됐나 반복문
        if(v[k][i] == true && !visited[i]){ // 연결이 되어있고, 방문하지 않았을 경우 방문
            dfs(i);
        }//if exit
    }//for exit
}//dfs exit

int main(){
    ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m >> start; // 노드, 간선, 시작점 input
    v.assign(n+1, vector<bool>(n+1, false)); // 2차원 Vector 초기화
    visited.assign(n+1, false); // Vector 초기화
    for(int i = 0; i < m; i++){ // 간선의 길이만큼 양방향 연결 
        int x,y;
        cin >> x >> y;
        v[x][y] = true;
        v[y][x] = true;
    }
    dfs(start);
}

graph.java

import java.util.*;
import java.io.*;

public class graph {

    static int n, m, start;
    static boolean[][] graph;
    static boolean[] visited;
    
    public static void dfs(int k){
        visited[k] = true;
        System.out.print(k + " ");
        for(int i = 1; i <= n; i++){
            if(graph[k][i] == true && !visited[i]){
                dfs(i);
            }
        }
    }

    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        start = Integer.parseInt(st.nextToken());
        graph = new boolean[n+1][n+1];
        visited = new boolean[n+1];
        for(int i = 0; i < m; i++){
            st = new StringTokenizer(br.readLine());
            int x,y;
            x = Integer.parseInt(st.nextToken());
            y = Integer.parseInt(st.nextToken());
            graph[x][y] = true;
            graph[y][x] = true;
        }
        dfs(start);
    }
}

input

6 5 1
1 2
1 3
2 4
2 5
3 6

output

1 2 4 5 3 6 

---

너비 우선 탐색

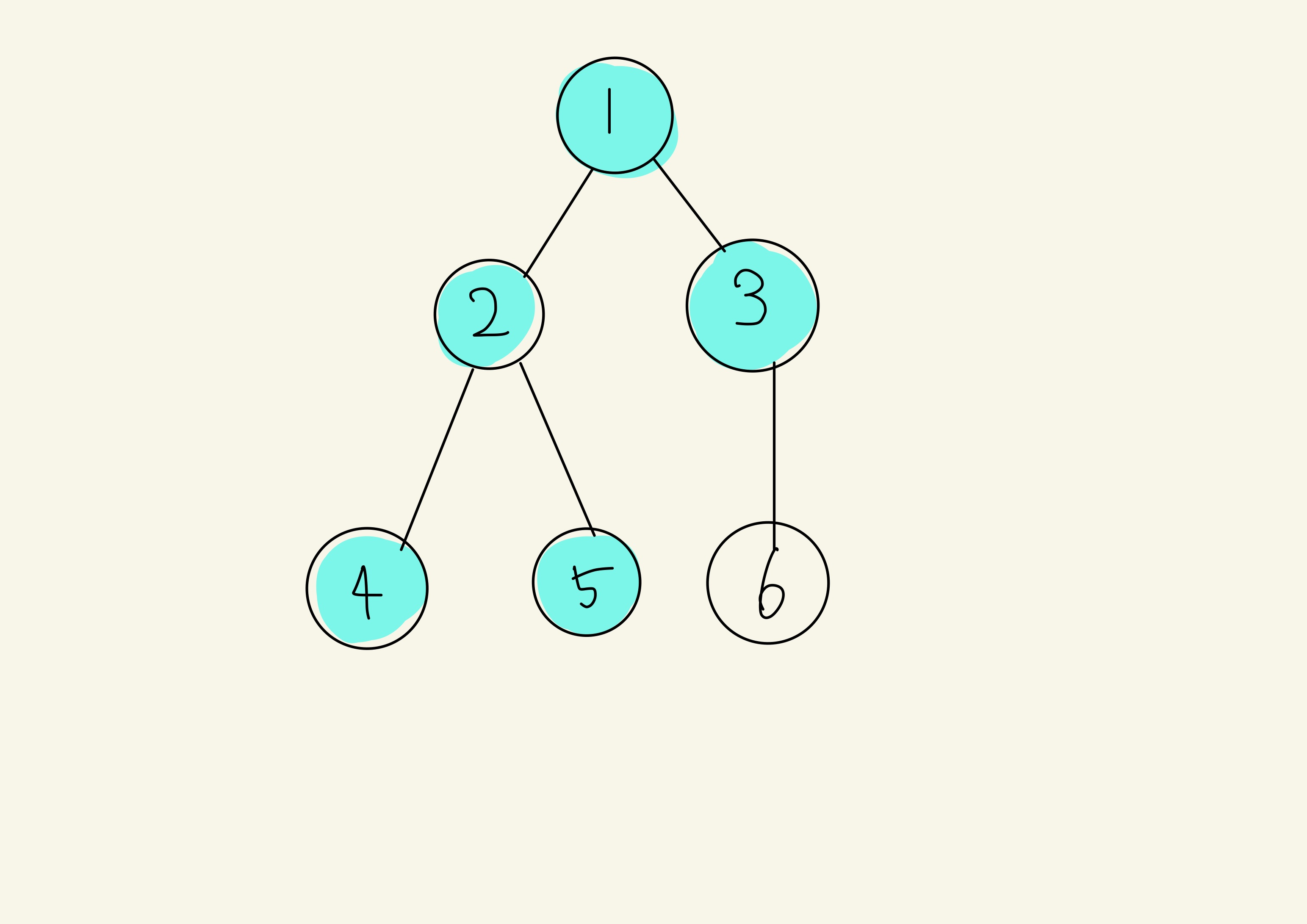
너비 우선 탐색은 너비를 우선으로 탐색하는 알고리즘입니다. 너비 우선 탐색은 Queue 자료구조를 사용합니다. 다음 그림을 보면서 설명을 드리겠습니다. 첫번째 사진은 dfs와 같습니다. 시작점은 1로 시작하겠습니다.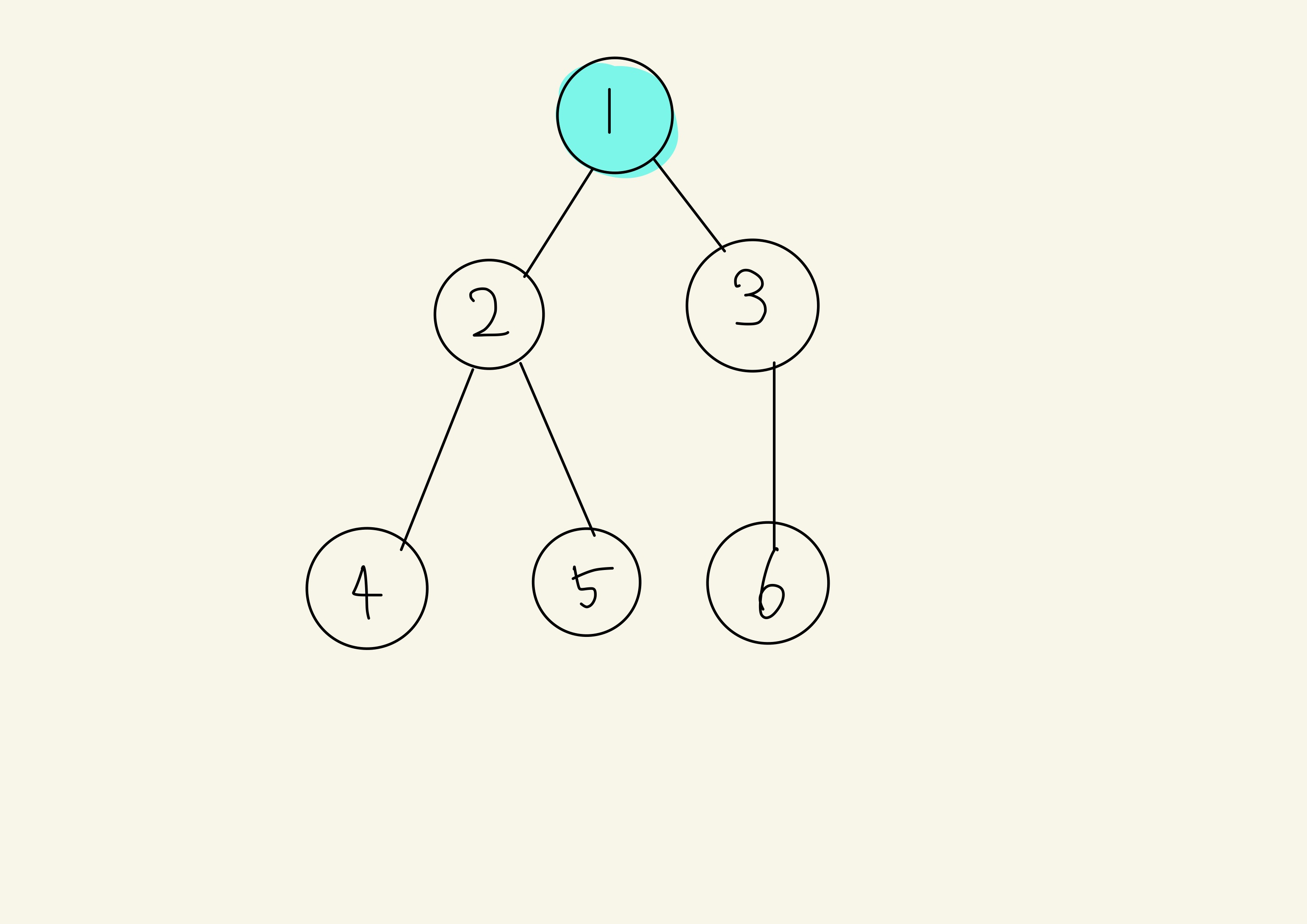

1을 방문했기 때문에 방문처리 해주고, 1의 자식 2와 3을 queue에 offer 해줍니다.
그 다음은 1의 자식은 없기에 queue에 있는 2를 방문합니다.

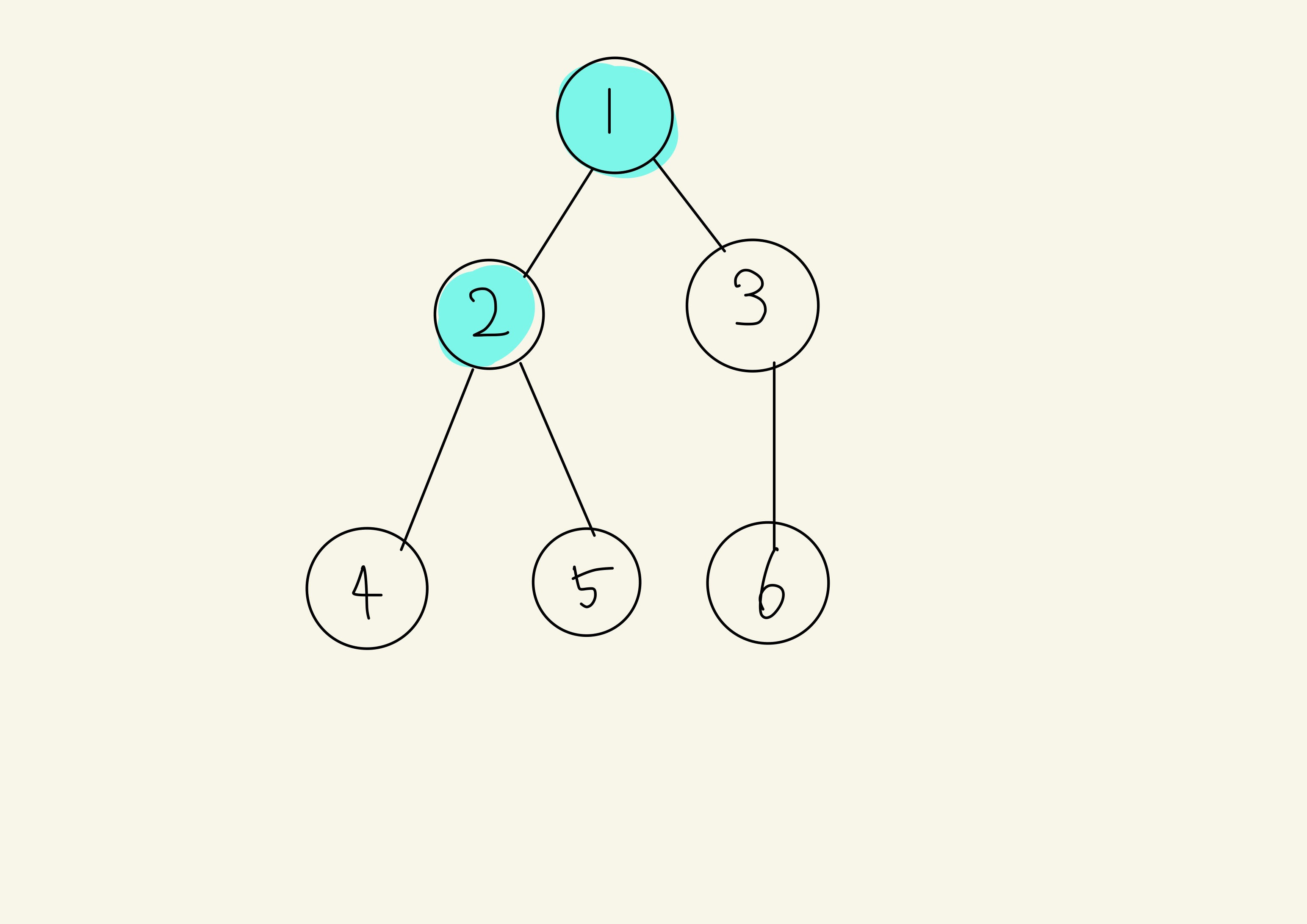
2를 방문한 뒤 방문처리를 해주고, 2의 자식인 4와 5를 offer한 후 다음과정으로 넘어갑니다.

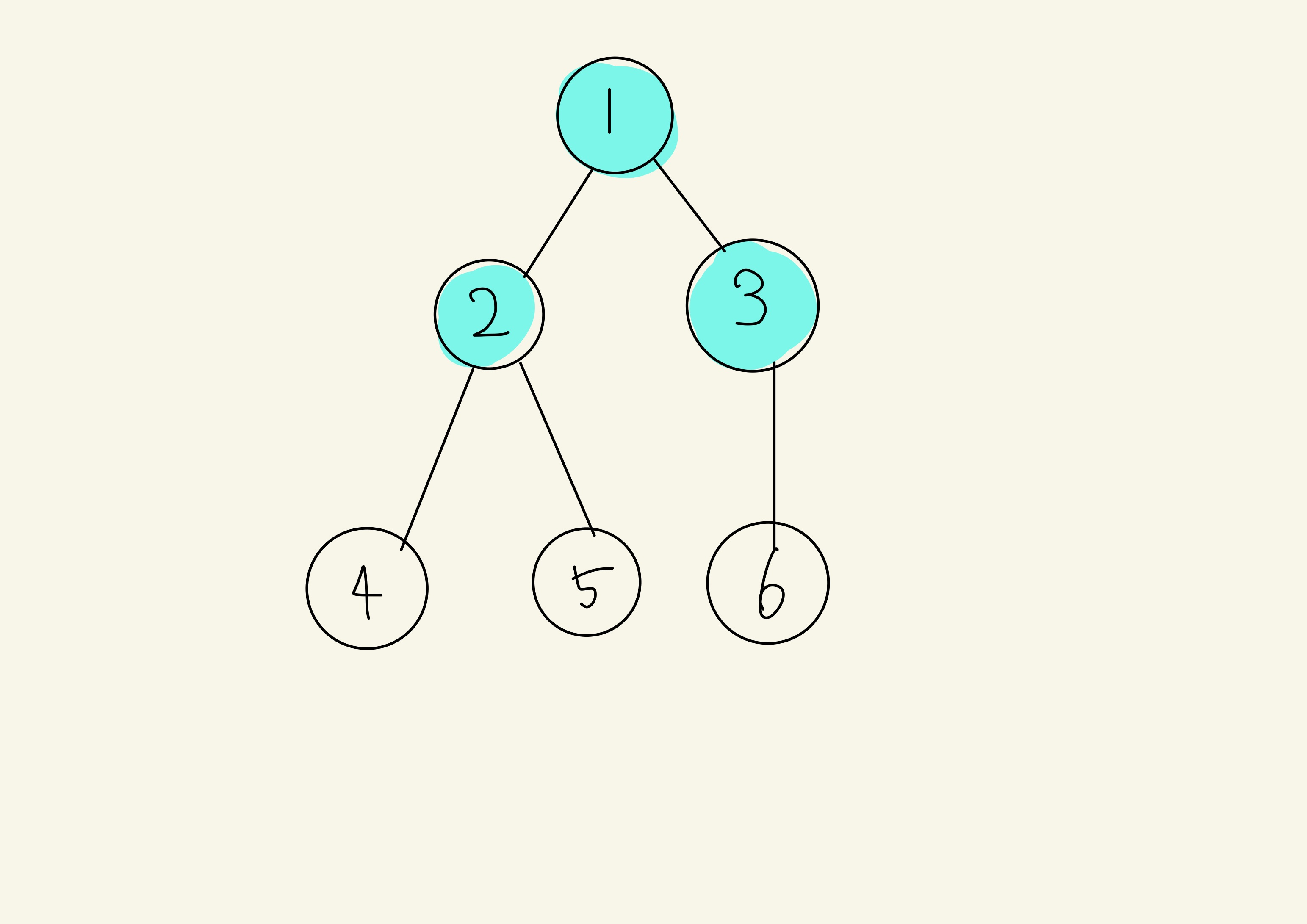
자료구조 Queue를 이용했기에 다음 과정은 3이 나옵니다.
3의 자식인 6을 queue에 offer 해주고 다음과정으로 넘어갑니다.

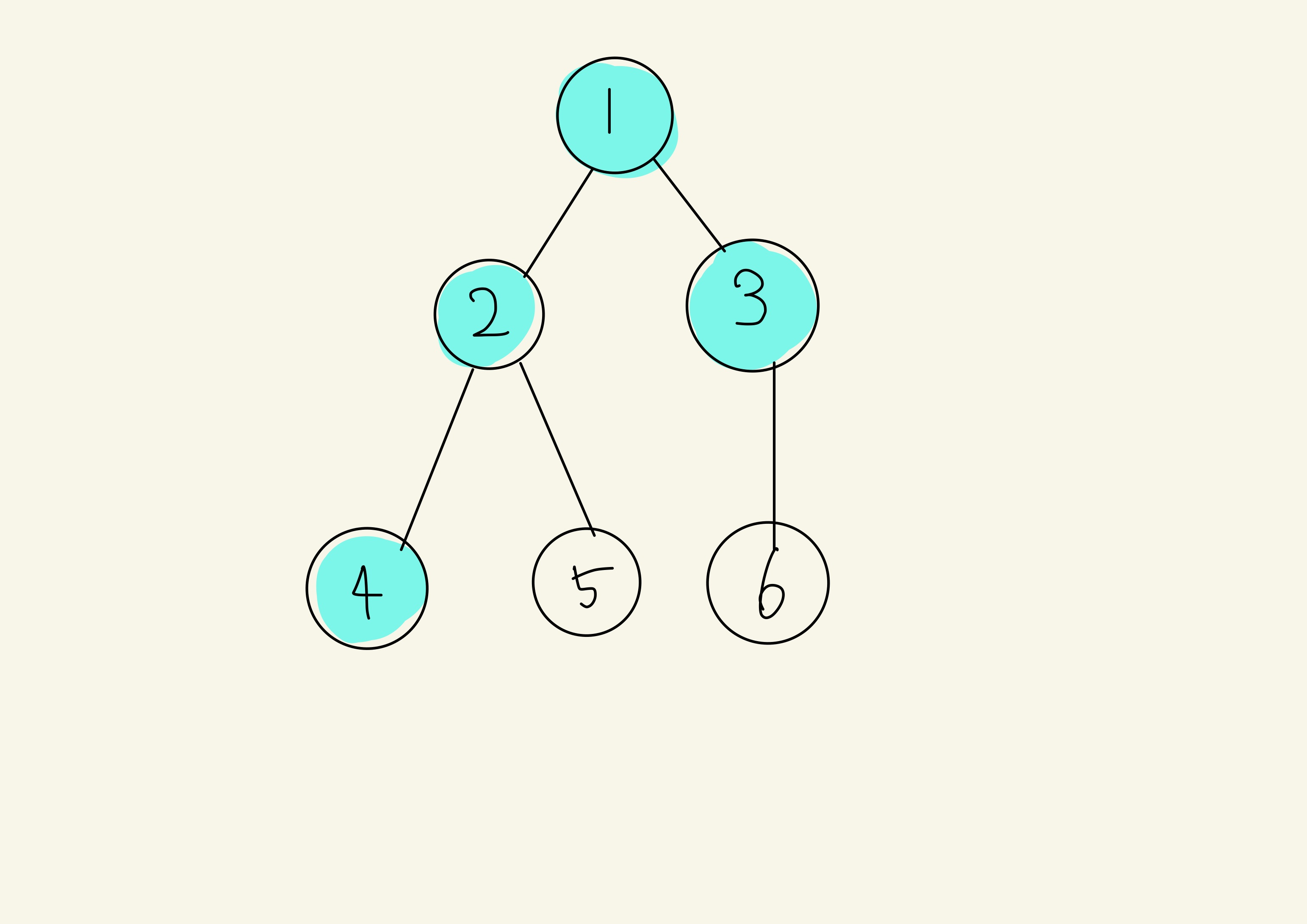
그 다음은 queue에 들어간 순서대로 4를 방문해 주고 방문처리를 해줍니다.
4는 자식이 없기에 다음으로 넘어갑니다.

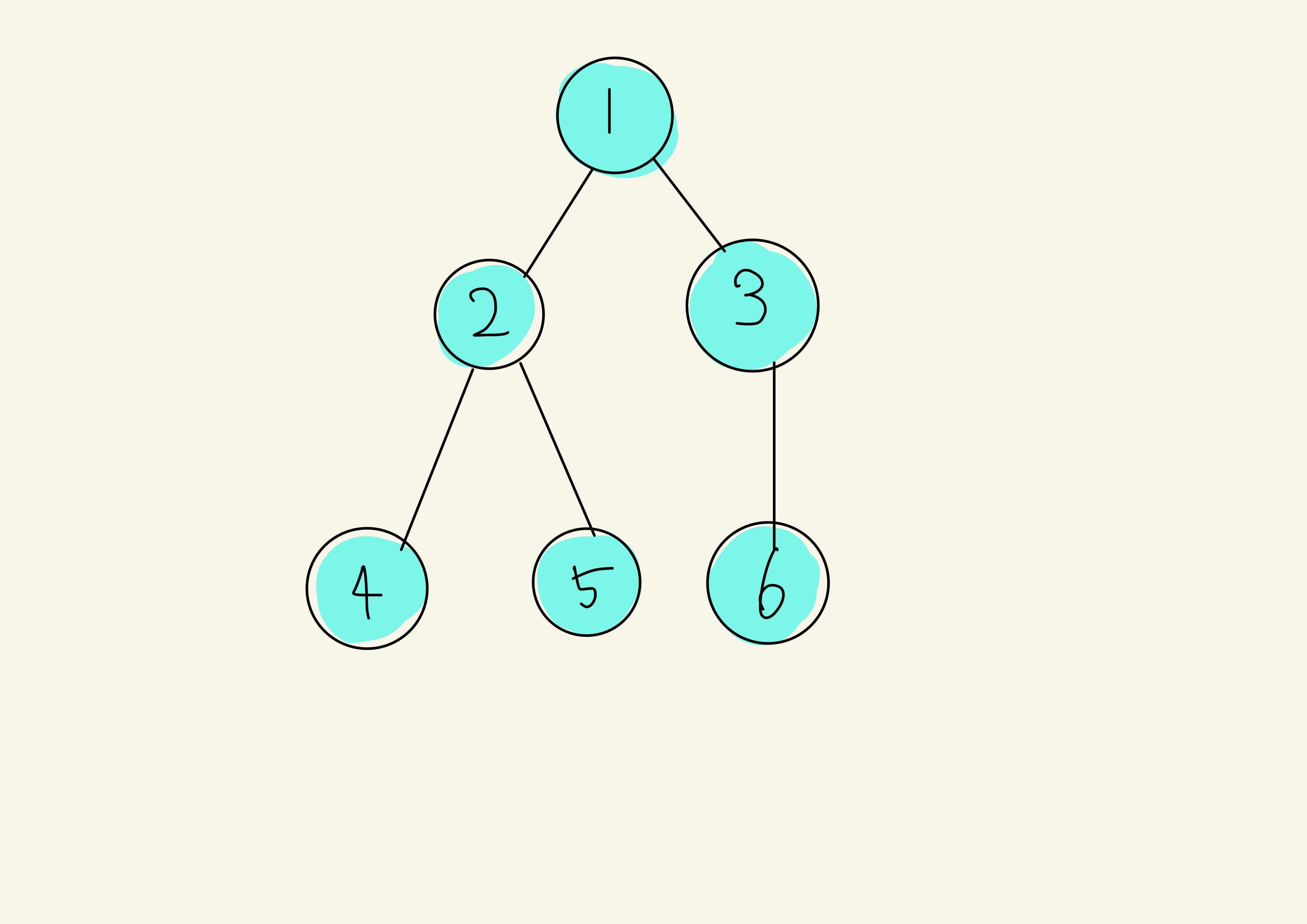
5와 6도 4와 같은 과정을 가집니다.

이를 코드로 보면 다음과같습니다
C++

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define endl '\n'
using namespace std;

vector<vector<bool> > v;
vector<bool> visited;
int n, m, start;
queue<int> q;

void bfs(){ // 넓이 우선 탐색
    q.push(start); // 넓이우선은 Queue 자료구조를 사용하고 시작점을 push, 방문처리 후 시작 
    visited[start] = true; // 방문처리 순서중요 
    while(!q.empty()){ // q가 비어있지 않으면 계속 반복 
        int k = q.front(); // 넣은 순서대로 탐색이기 때문에 front 받고
        cout << k << " "; //출력
        q.pop(); // C++은 pop을 해도 값을 안뱉기 때문에 위와같이 front를 해준 뒤 따로 pop
        for(int i = 1; i <= n; i++){ // bfs와 같은 로직 
            if(v[k][i] == true && !visited[i]){
                q.push(i); // 조건 성립시 push
                visited[i] = true; // 방문처리 순서중요 : push할 때 방문처리를 하지 않으면 중복해서 push를 하여 다른 결과값을 받을 수 있음
            }
        }
    }
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m >> start; // 노드, 간선, 시작점 input
    v.assign(n+1, vector<bool>(n+1, false)); // 2차원 Vector 초기화
    visited.assign(n+1, false); // Vector 초기화
    for(int i = 0; i < m; i++){ // 간선의 길이만큼 양방향 연결 
        int x,y;
        cin >> x >> y;
        v[x][y] = true;
        v[y][x] = true;
    }
    bfs();
}

graph.java

import java.util.*;
import java.io.*;

public class graph {

    static int n, m, start;
    static boolean[][] graph;
    static boolean[] visited;
    static Queue<Integer> q = new LinkedList<>();

    public static void bfs(){
        q.offer(start);
        visited[start] = true;
        while(!q.isEmpty()){
            int k = q.poll();
            System.out.print(k + " ");
            for(int i = 1; i <= n; i++){
                if(graph[k][i] == true && !visited[i]){
                    q.offer(i);
                    visited[i] = true;
                }
            }
        }
    }

    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        start = Integer.parseInt(st.nextToken());
        graph = new boolean[n+1][n+1];
        visited = new boolean[n+1];
        for(int i = 0; i < m; i++){
            st = new StringTokenizer(br.readLine());
            int x,y;
            x = Integer.parseInt(st.nextToken());
            y = Integer.parseInt(st.nextToken());
            graph[x][y] = true;
            graph[y][x] = true;
        }
        bfs();
    }
}

input

6 5 1
1 2
1 3
2 4
2 5
3 6

output

1 2 3 4 5 6 

---

다음은 백준에 있는 그래프 순회중 가장 기초문제입니다.
https://www.acmicpc.net/problem/1260