[24.04.20]게임수학 - 벡터 : 가상 공간의 탄생

교재 : 이득우의 게임수학

3.2 벡터 공간과 벡터

직선의 수 집합을 수직으로 배치해 평면을 표깋는 방식을 데카르트 좌표계(Cartesian coordinate system) 라고 부른다. 곱집합의 원어가 데카르트 곱(Cartesian product)임을 생각해본다면 이 둘은 동일한 개념임을 알 수 있다.

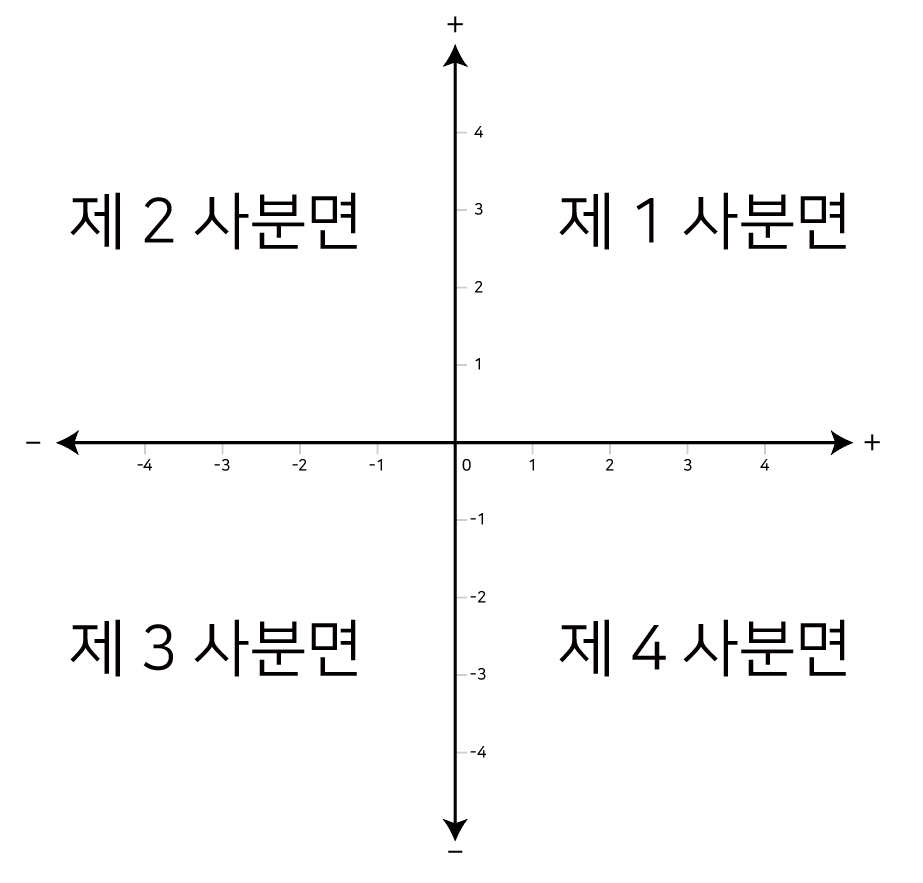
데카르트 좌표계의 한 원소는 곱집합과 동일하게 순서쌍으로 표현하며 좌표(Coordinate)라고 부른다.

(x, y)

좌표의 시각화 방법

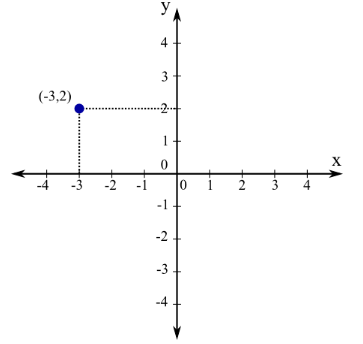
3.2.1 스칼라와 벡터

두 개 이상의 실수를 곱집합으로 묶어 형성된 집합을 공리적 집합론의 관점에서 규정한 것을 벡터 공간(Vector space)이라고 하며, 벡터 공간의 원소를 벡터(Vector)라고 한다.

체의 구조를 가지는 수 집합의 원소를 스칼라(Scalar) 라고 부른다.
벡터는

v = (x, y)

과 같이 표기한다.

3.2.2 벡터 공간의 연산

벡터와 벡터의 덧셈(벡터의 합)

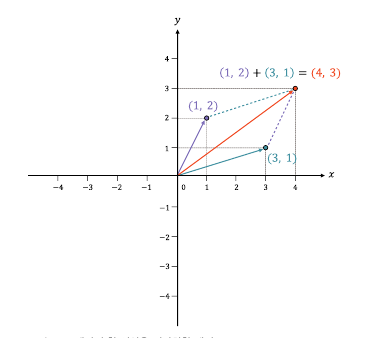
스칼라와 벡터의 곱셈(스칼라 곱셈)

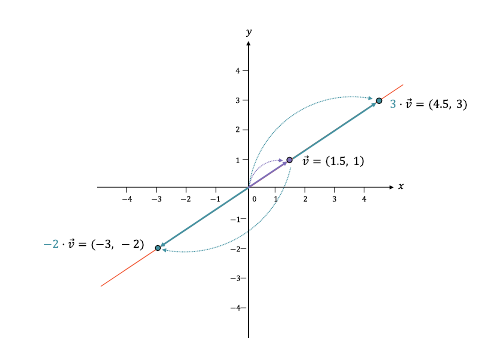
스칼라 곱셈의 시각적 의미를 살펴보면 , 스칼라 곱셈으로 생성된 벡터는 원점을 지나고 벡터와 평행한 직선상에 위치한다. 따라서 스칼라 곱셈의 결과는 항상 그림처럼 붉은색으로 표현한, 원점을 지나는 직선상의 벡터를 만들어낸다.

프로그래밍 으로 벡터의 합과 스칼라 곱셈 연산을 구현한 코드

float scalar = 10f;
Vector2 vec(2.f, 3.f);
Vector2 vec(4.f, 5.f);

Vector2 addition = vec1 + vec2; // (6, 8)
Vector2 multiplication = vec1 * scalar; // (20, 30)

참고 : 벡터와 스칼라의 곱을 표현하기 위해 이책(이득우의 게임수학)에서 사용한 스칼라의 곱셈은 스칼라배(Scalar倍) 라고도 불린다.
스칼라곱이라는 용어가 있는데, 이는 스칼라 곱셈과 다른 연산이며 7장에서 다루는 내적 을 의미한다.