📚 Data Structure : 자료구조

프로그램이란, 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것입니다. 이때, 데이터의 표현은 데이터의 저장을 포함하는 개념이며, 데이터의 저장을 담당하는 것이 자료구조입니다.

Algorism

알고리즘은 자료구조 등으로 표현 및 저장된 데이터를 대상으로 하는 문제의 해결방법입니다.
자료구조에 따라 효율적인 알고리즘은 달라집니다.

그렇다면 어떻게 해당 알고리즘이 효율적인지 알 수 있을까?

💻 Performance Analysis : 성능 분석

시공간적 측면에서 machine-independent 가 어떠한지 추정하기 위해 분석합니다.

알고리즘을 평가하는 중요한 두가지 요소

Space complexity : 공간 복잡도

• 프로그램이 필요로 하는 메모리 공간의 양
• S(p) = c + Sp(n)

고정 공간(Fixed Part, c) : 프로그램 입출력의 횟수나 크기와 관계없는 공간
ex) 변수, 구조체, 상수

가변 공간(Variable Part, Sp(n)) : 특정 instance 특성에 의존하는 크기를 가진 구조화 변수들을 위해 필요한 공간. 즉 크기가 변할 수 있다.
공간 복잡도에 직접 관여
ex) dynamic memory allocation, using stacks for recursion

instance 특성이란? 어떤 선언된 객체가 실제로 값이 할당된 소프트웨어 상의 실체를 말합니다

Time compexity : 시간 복잡도

• 프로그램을 실행시키는데 소요되는 시간
• T(P) = c + Tp(n)

컴파일 시간(compile time, c) : 인스턴스 특성에 의존하지 않습니다. -> 시간 복잡도 상관 x

실행 시간(run time, Tp(n)) : 시간복잡도를 결정

👨‍💻어떻게 분석할까?

분석 방법을 알기 위해서는 먼저 Program Step의 개념을 알아야 합니다.

Program Step(프로그램 단계)

말 그대로 프로그램의 문법적인 혹은 논리적인 단위

• 실행시간이 인스턴스 특성에 구문적으로 또는 의미적으로 독립성을 같는 프로그램의 단위입니다.

• assignment, calculate, 입출력, return문 등

• 선언문은 해당하지 않습니다!

T(P) = 2n + 3

• 각각의 steps의 frequency를 판단하고 전체 코드의 step을 판단합니다.
• 주의할 점은 for문 같은 반복문의 step을 생각할 때 조심해야 합니다.

이러한 방식은 문제가 있습니다.
일일이 생각하기 어려울 뿐만 아니라
결정적으로 여러개의 코드들의 시간 복잡도 비교가 어렵습니다.
따라서 똑똑한 사람들이 새로운 정의 방법을 도입하였습니다.

Asymptotic notation(점근 표기법)

Big-O 표기법

다른 표기법들이 있지만 가장 많이 쓰이는 빅-오 표기법만 정리하였습니다.

• 함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 |f(n)| ≤ c |g(n)|을 만족하는 상수 c와 n0이 존재하면, f(n) = O(g(n))이다.

이해 하기가 어려운데 예를 들어 쉽게 설명하자면

f(n) = 100n 이라는 함수와 g(n) = n 이라는 함수가 있다고 생각합니다.
만약 g(n)이라는 함수에서 1000을 곱한다면 당연히 그래프에서 f(n)보다 가파르기 때문에
T(p) = 100n 은 O(n)으로 표기할 수 있습니다.

즉, 프로그램의 계산 시간이 많아봐야 c * n이하라 O(n)으로 표기할 수 있는 겁니다.
upper bound개념으로 가장 최악의 경우의 시간 복잡도라고 생각하면 됩니다.

그렇다면 해당 함수의 시간 복잡도를 분석해 본다면,

int sum(int list[], int n) {
	int sum = 0; // step: 1 freq: 1 total step: 1
	int i; // step 0 freq 0 total step : 0
	for (i = 0; i < n; i++) { // step: 1 freq: n + 1 total step: n + 1
		sum += list[i]; // step: 1 freq: n total step: n
	}
	return sum; // step: 1 freq: 1 total step: 1
}

total step = 2n + 3 이고 시간 복잡도는 O(n)이라 할 수 있습니다.

분석할 경우 반복문을 제외한 나머지 부분은 Big-O표기에서 상수 처리되기 떄문에 무시됩니다.
따라서 for문이나 while문 같은 반복문 위주로 분석하면 됩니다👍

비교 방법

알고리즘의 시간복잡도를 빅-오 표기법으로 나타낸 것 입니다.

O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)

크기가 작을수록 시간 복잡도가 작고 효율적인 알고리즘임을 알 수 있습니다.

직접 그래프를 생각해 본다면 당연함을 쉽게 판단할 수 있습니다.

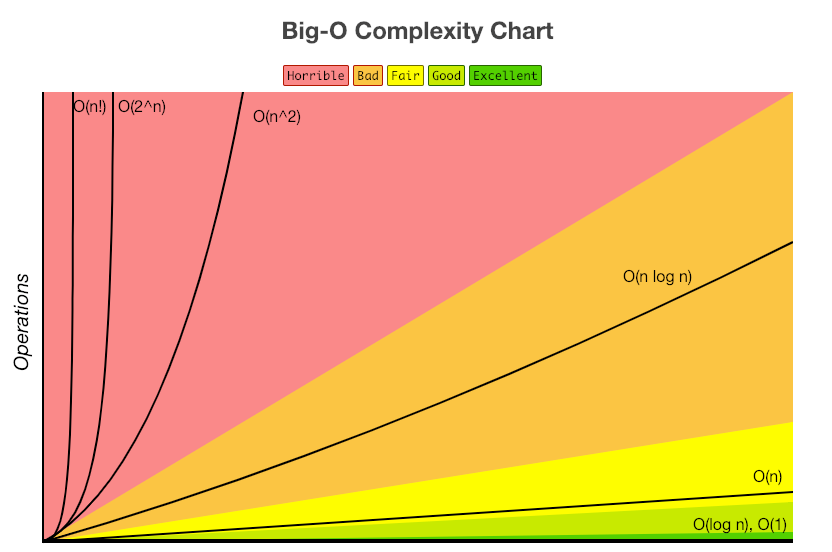
빅오 표기법을 사용한다면 더 효율적으로 알고리즘의 효율성을 판단할 수 있습니다👍