약수
inputNumber = int(input('0보다 큰 정수 입력: '))
for number in range(1, (inputNumber + 1)):
if inputNumber % number == 0:
print('{}의 약수: {}'.format(inputNumber,number))
소수
- 1과 자신만을 약수로 가지는 수 (단, 1은 제외)
inputNumber = int(input('0보다 큰 정수 입력: '))
for number in range(2, (inputNumber + 1)):
flag = True
for n in range(2, number):
if number % n == 0:
flag = False
break
if (flag):
print('{} : 소수!!'.format(number))
else:
print('{} : 합성수!!'.format(number))
소인수
- 약수 (인수) 중에서 소수인 숫자를 소인수라고 한다.
inputNumber = int(input('1보다 큰 정수 입력: '))
n = 2
while n <= inputNumber:
if inputNumber % n == 0:
print('소인수: {}'.format(n))
inputNumber /= n
else:
n += 1
소인수분해
- 1보다 큰 정수를 수인수의 곱으로 나타낸 것을 소인수분해라고 한다.
inputNumber = int(input('1보다 큰 정수 입력: '))
n = 2
searchNumber = []
while n <= inputNumber:
if inputNumber % n == 0:
print('소인수: {}'.format(n))
if searchNumber.count(n) == 0:
searchNumber.append(n)
elif searchNumber.count(n) == 1:
searchNumber.remove(n)
inputNumber /= n
else:
n += 1
print('searchNumber: {}'.format(searchNumber))
소인수분해와 약수
- 소인수분해를 이용해서 약수를 정확하게 쉽게 구할수 있다.
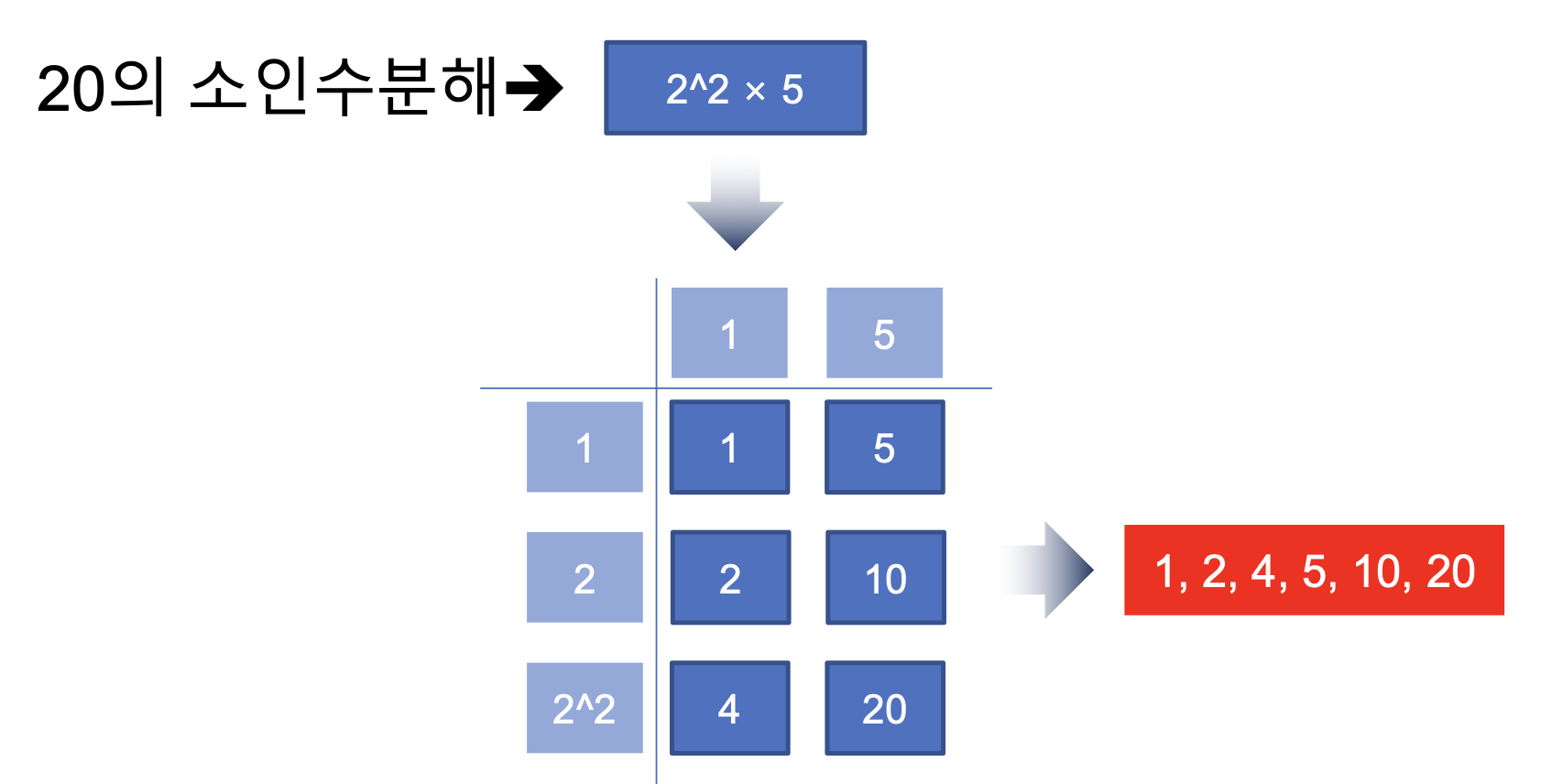
공약수
- 두 개 이상의 수에서 공통된 약수를 공약수라고 한다.
num1 = int(input('1보다 큰 정수 입력:'))
num2 = int(input('1보다 큰 정수 입력:'))
for i in range(1,(num1 + 1)):
if num1 % i == 0 and num2 % i == 0:
print('공약수: {}'.format(i))
최대공약수 (GCD)
- 공약수 중 가장 큰 수를 최대공약수라고 한다.
- 소인수분해를 이용하면 최대공약수 및 공약수를 구할수 있다.
- 소수로 나눗셈 해서 편리하게 최대공약수를 구할수 있다.
num1 = int(input('1보다 큰 정수 입력:'))
num2 = int(input('1보다 큰 정수 입력:'))
maxNum = 0
for i in range(1,(num1 + 1)):
if num1 % i == 0 and num2 % i == 0:
print('공약수: {}'.format(i))
maxNum = i
print('최대공약수: {}'.format(maxNum))
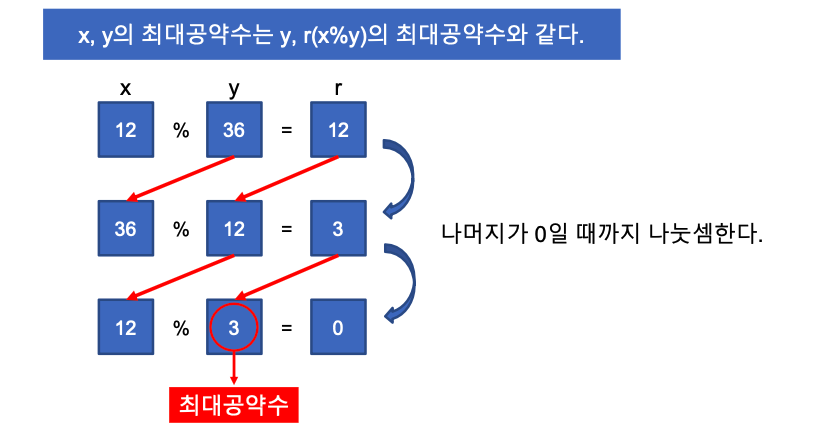
유클리드 호제법
- 유클리드 호제법을 이용해서 최대공약수를 구할 수 있다.
num1 = int(input('1보다 큰 정수 입력:'))
num2 = int(input('1보다 큰 정수 입력:'))
temp1 = num1
temp2 = num2
while temp2 > 0:
temp = temp2
temp2 = temp1 % temp2
temp1 = temp
print('{}, {}의 최대공약수: {}'.format(num1,num2,temp1))
for n in range(1, (temp1 + 1)):
if temp1 % n == 0:
print('{},{}의 공약수: {}'.format(num1, num2, n))
공배수
- 두 개 이상의 수에서 공통된 배수를 공배수라고 한다.
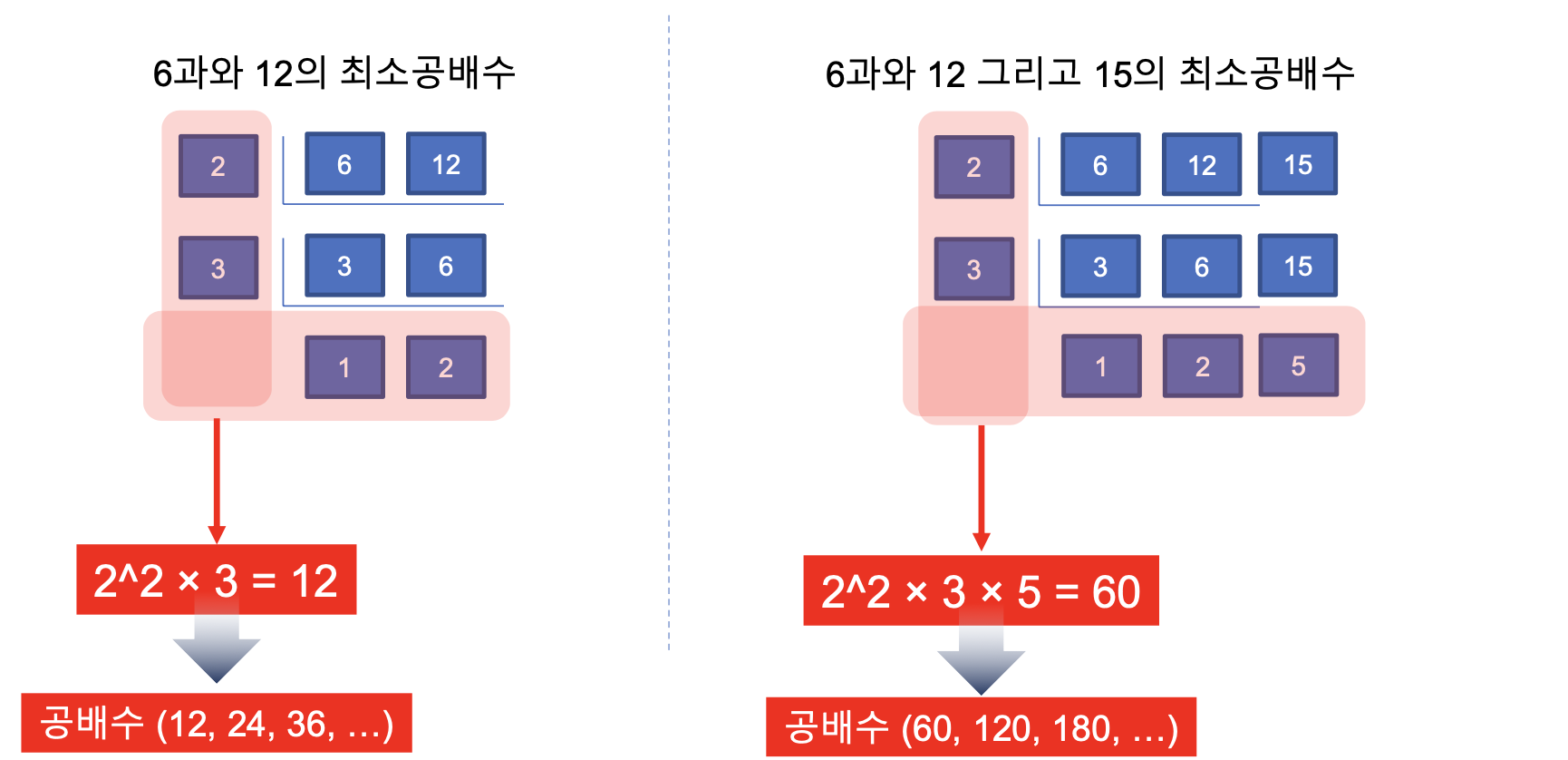
최소공배수
- 소인수분해를 이용하면 최소공배수 및 공배수를 구할 수 있다.

- 좀 더 편리하게 최소공배수 구하는 방법! 소수로 나눗셈 하자!
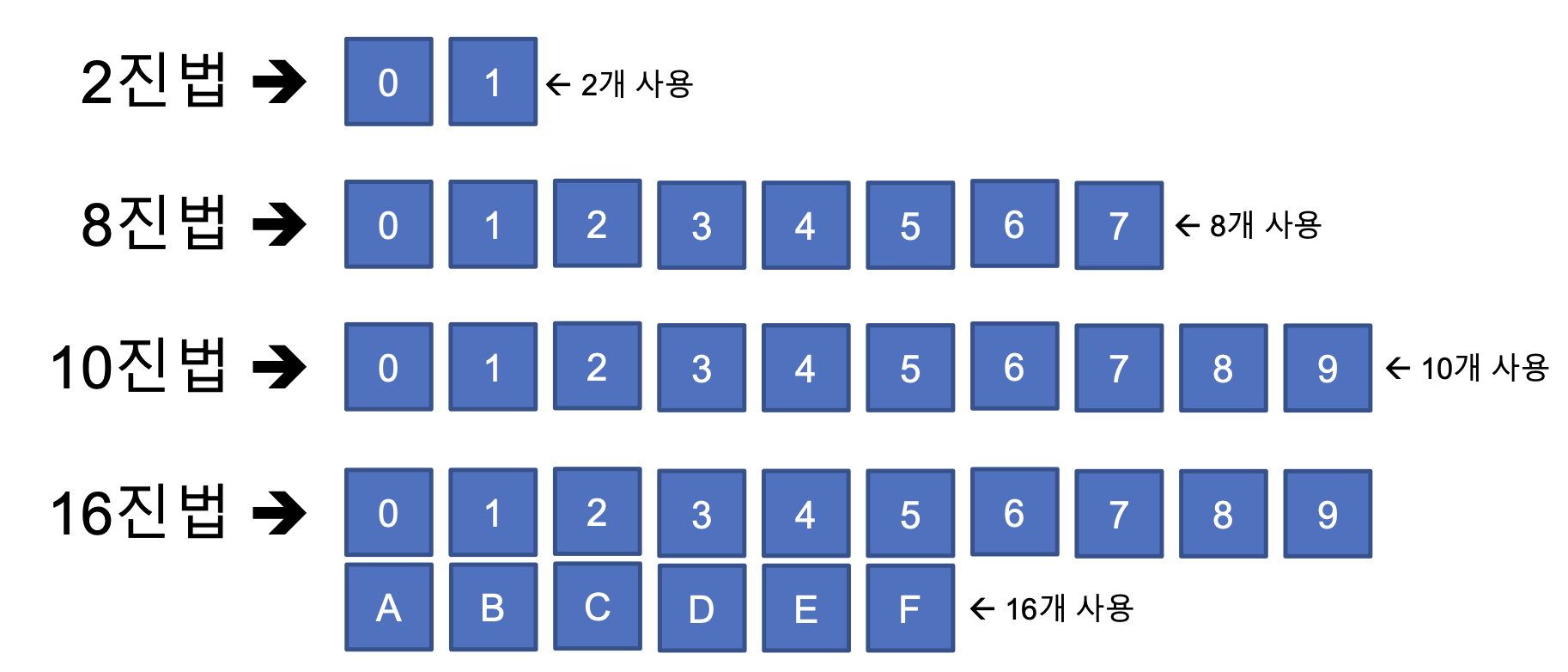
진법
- 특정 숫자 몇 개를 사용하여 수를 표시하는 방법이다.
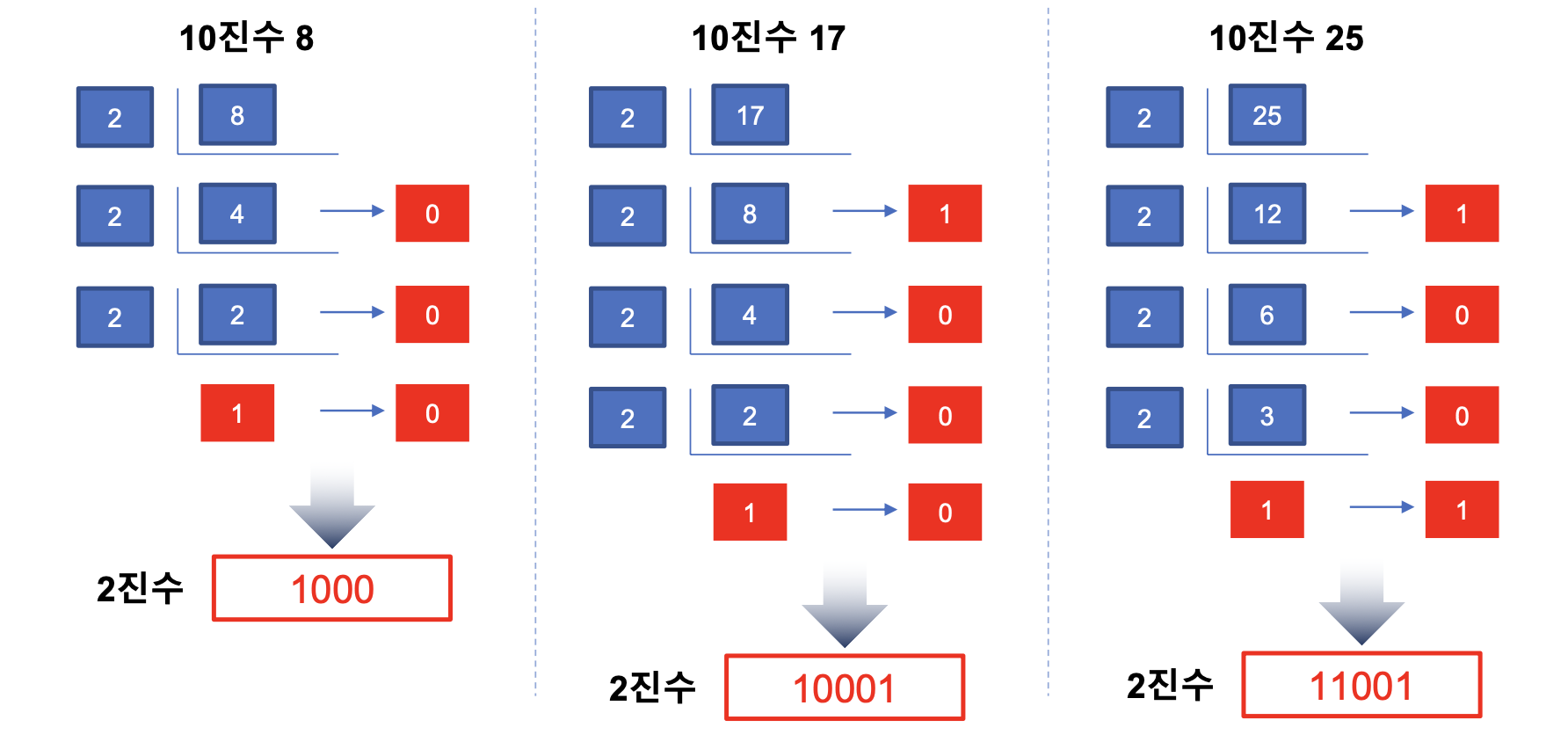
10진수를 X진수로 변환
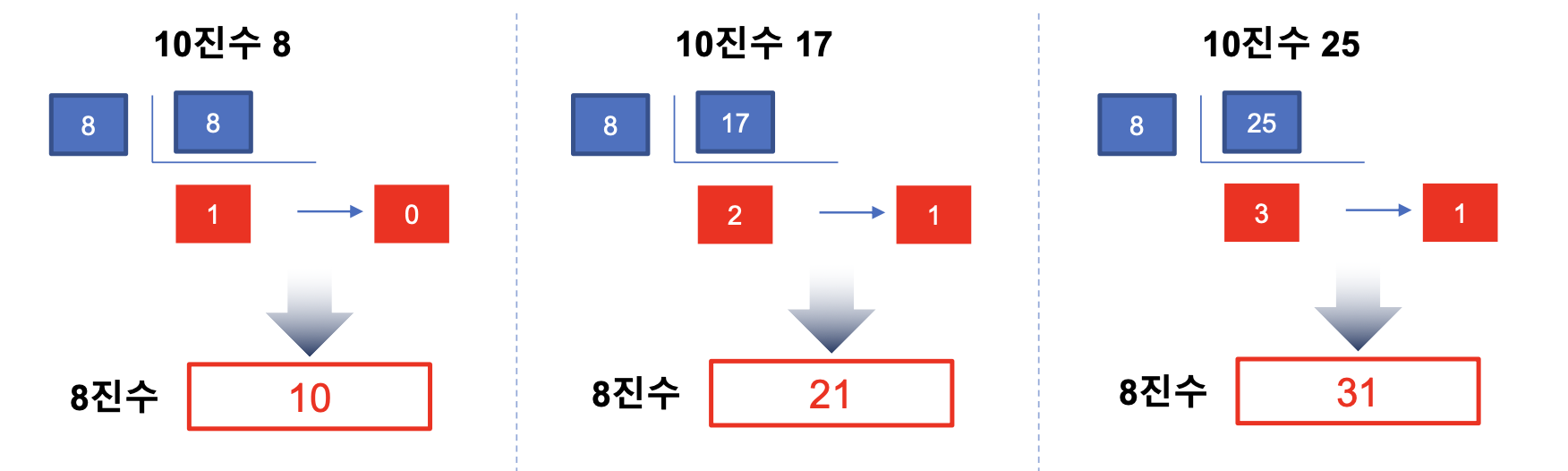

X진수를 10진수로 변환

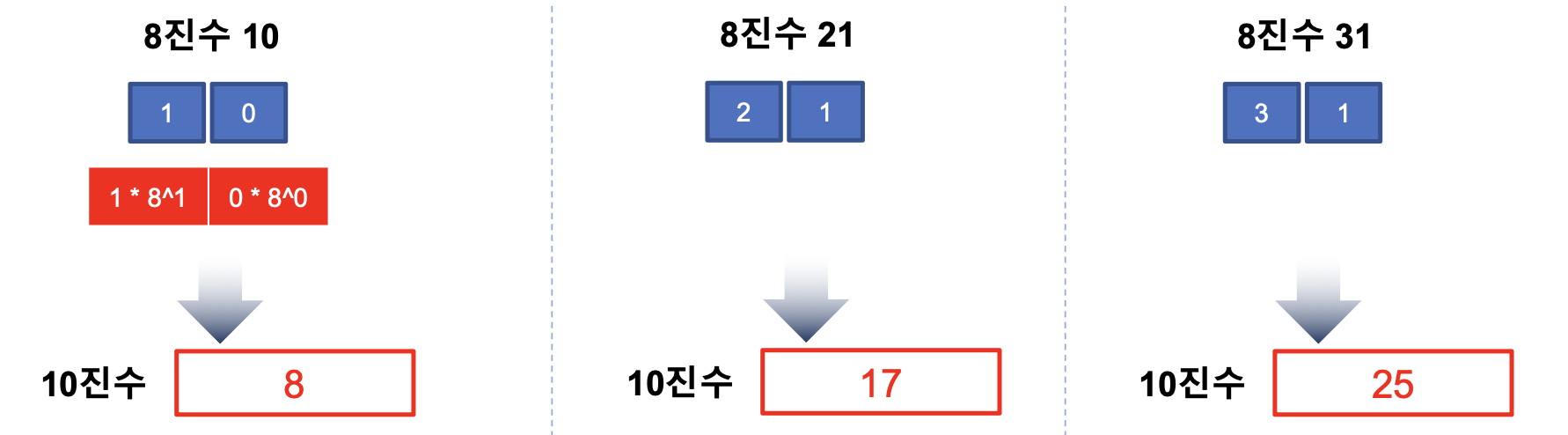
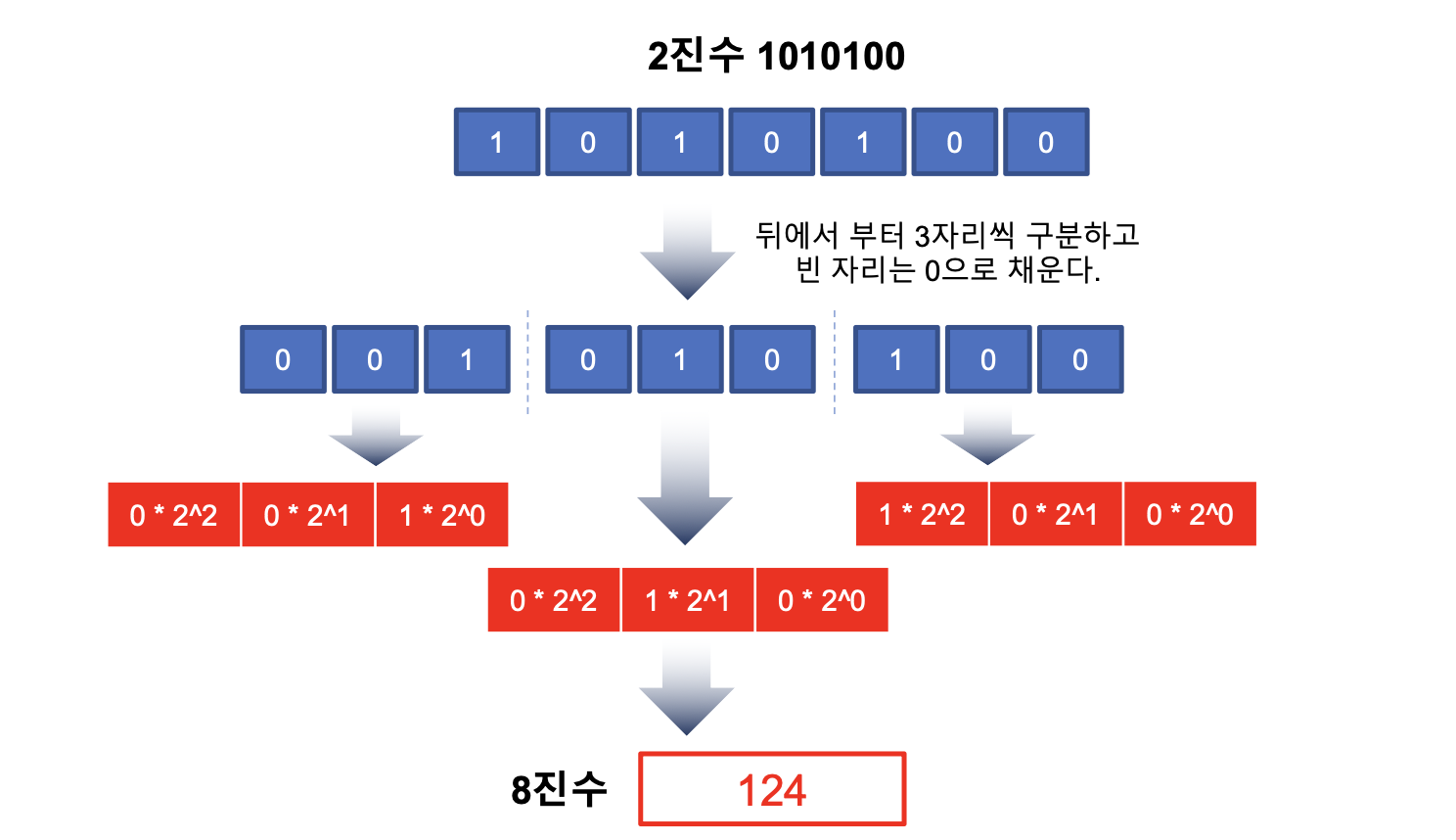
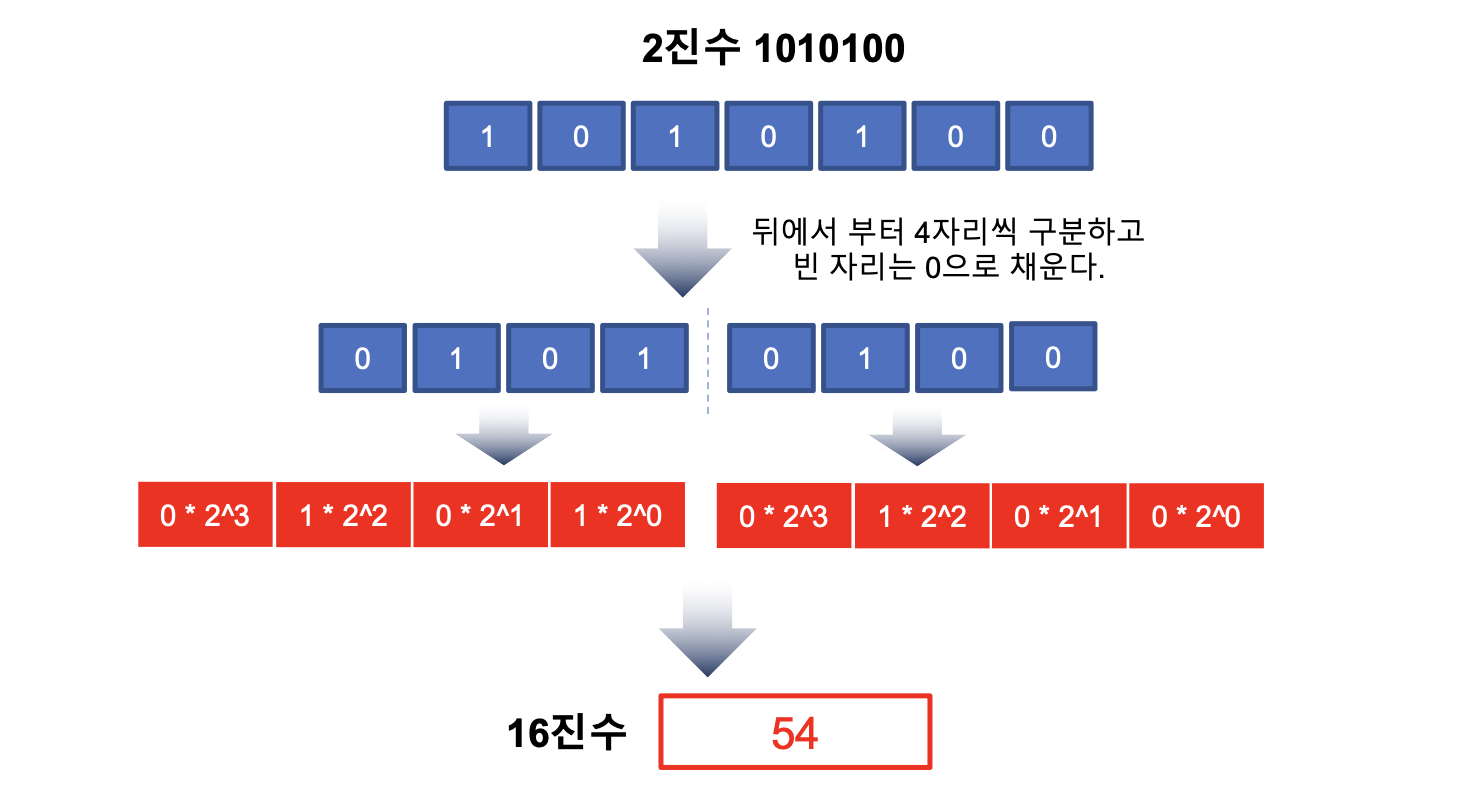
2진수를 X진수로 변환