Problem
Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].
The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:
The rank is an integer starting from 1.
If two elements p and q are in the same row or column, then:
If p < q then rank(p) < rank(q)
If p == q then rank(p) == rank(q)
If p > q then rank(p) > rank(q)
The rank should be as small as possible.
It is guaranteed that answer is unique under the given rules.Example 1:
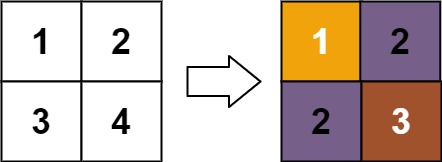
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.
Example 2:
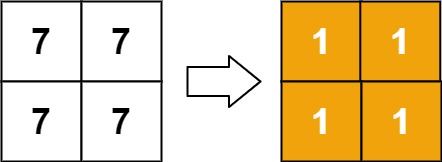
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]
Example 3:
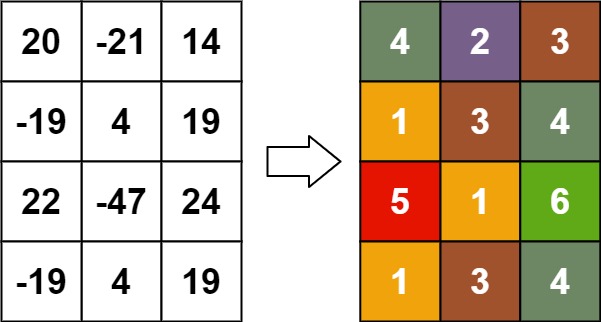
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
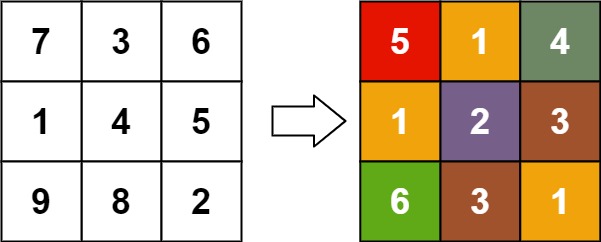
Example 4:Input: matrix = [[7,3,6],[1,4,5],[9,8,2]] Output: [[5,1,4],[1,2,3],[6,3,1]]
Constraints:・ m == matrix.length ・ n == matrix[i].length ・ 1 <= m, n <= 500 ・ -109 <= matrix[row][col] <= 109
Idea
Palindrome 문제도 어렵다고 생각했는데, 그것과는 비교도 안 될 난이도의 문제가 나왔다. 작은 값부터 순차적으로 rank를 매기면 된다는 것까진 알았지만 복잡하게 풀었더니 결국 몇 가지 Test Case에서 실패하고 말았다. row와 column의 랭크를 각각의 dp에 저장해서 활용했는데, 이럴 경우 같은 값이 몇 개의 row와 column에 걸쳐 있는 경우 rank를 제대로 매기지 못한다. 결국 관건은 같은 값을 가진 cell이 같은 row 또는 같은 column에 걸쳐 있는 경우 이를 어떻게 grouping하고 같은 rank를 줄 것인지에 달려있다.
알고리즘 순서는 다음과 같다.
- matrix의 각 element의 value, row index, column index를 priority queue에 저장한다.
- value가 같은 element를 grouping하기 위해 값을 설정한다.
- 2번 단계에서 설정한 값을 key로 하여 각 element를 map에 넣는다.
- 같은 group마다 rank를 계산하여 group의 각 element에 rank를 부여한다.
위와 같은 방법으로 문제를 풀면, 서로 다른 row 또는 column에 걸쳐 있으면서 같은 값을 가진 element에 같은 rank를 부여할 수 있다. priority queue에 넣어 element를 정렬하는 건 쉽다. grouping하는 알고리즘을 이해하기가 까다로운데, 같은 row뿐 아니라 같은 column에 속한 element에 같은 group index를 부여해야 하기 때문이다.
3x3 matrix를 예를 들어보자. 만약 (0,0) index와 (0,1) index, (1,1) index, (2,2) index가 같은 값을 가지고 있다고 하자. 그러면 (0,0),(0,1),(1,1)이 같은 group에 속해 있어야 하며, (2,2) index는 다른 group에 속해 있어야 한다. 왜냐하면 같은 값을 가지고 있더라도 (2,2) index는 row와 column이 아예 달라 rank 또한 달라져야 하기 때문이다.
여기서는 column 값을 group의 index로 정했다. 각 column값에 row의 길이를 더해 row와 column의 group index를 똑같이 맞춰준다. group의 index를 구하기 위해 다음과 같은 알고리즘을 활용했다.
fun f(x): Int { if (f[x] == x) return f[x]; return f[x] = find(f[x]); } if find(row) != find(column + m) then f[row] = find(column + m)
(0,0)의 경우 row 0과 column 0을 기준으로 rank를 정해야 한다. row의 길이가 3이므로 f[0] = f[0+3] = 3으로 정한다. (0,1)의 경우 row 0과 column 1이 기준이다. (f[0] = f[1+3] = 4) (1,1)의 경우 row 1과 column 1이 기준이 된다. (f[1] = f[4] = 4) (2,2)는 row 2와 column 2로 값을 구하면 f[2] = f[2+3] = 5가 되므로 다른 group에 속하게 된다. 즉, row 또는 column이 같은 element의 경우 (row의 길이) + (같은 값을 가진 element의 column 최대값)이 group index가 된다.
group index를 기준으로 map에 각각의 element를 저장한 뒤, rank를 구한다. Dynamic programming을 적용해 각 row와 column의 최대값을 저장해 둔다. rank는 row와 column의 최대값에 1을 더한 값과 현재 rank의 값을 비교하여 더 큰 값으로 정하면 된다. rank를 구했으면 group에 속한 모든 element에 rank를 저장한 뒤, dp (row와 column의 최대값)에도 rank를 저장한다. Priority Queue가 빌 때까지 위 과정을 반복하면 리턴할 matrix의 모든 cell을 채울 수 있다.
풀이를 이해하는 데만 한참이 걸렸지만, 이런 어려운 문제를 이해하고 나면 뿌듯하다. 귀중한 일요일 저녁 시간 제대로 쉬지도 못 했지만 비슷한 유형의 문제가 나오면 오늘 배웠던 알고리즘을 적용해 볼 수 있었으면 좋겠다😄.
Solution
class Solution { int[] f; // for grouping public int[][] matrixRankTransform(int[][] matrix) { int m = matrix.length; int m = matrix.length; int n = matrix[0].length; f = new int[m+n]; int[] row = new int[m]; // max rank of each row int[] col = new int[n]; // max rank of each column int[][] ret = new int[m][n]; PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]); // 1. sort elements with row index and column index for (int i=0; i < m; i++) for (int j=0; j < n; j++) q.add(new int[]{matrix[i][j], i, j}); while (!q.isEmpty()) { int target = q.peek()[0]; List<int[]> array = new ArrayList<>(); while (!q.isEmpty() && q.peek()[0] == target) array.add(q.poll()); // 2. determine grouping index for (int i=0; i < m+n; i++) f[i] = i; for (int[] a : array) { int t1 = find(a[1]); int t2 = find(a[2] + m); if (t1 != t2) f[t1] = t2; } // 3. grouping elements with the same value and the same rank Map<Integer, List<int[]>> map = new HashMap<>(); for (int[] a : array) { if (!map.containsKey(find(a[1]))) map.put(find(a[1]), new ArrayList<>()); map.get(find(a[1])).add(a); } // 4. set rank of each elements for(List<int[]> group : map.values()) { int rank = 0; for (int[] element : group) { rank = Math.max(rank, Math.max(row[element[1]], col[element[2]])+1); } for (int[] element : group) { ret[element[1]][element[2]] = rank; row[element[1]] = rank; col[element[2]] = rank; } } } return ret; } private int find(int x) { if (f[x] == x) return f[x]; return f[x] = find(f[x]); } }
Reference
https://leetcode.com/problems/rank-transform-of-a-matrix/
https://www.fatalerrors.org/a/java-programming-rank-after-matrix-transformation-leetcode-1632.html