[leetcode #1008] Construct Binary Search Tree from Preorder Traversal

Problem

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

Example 1:

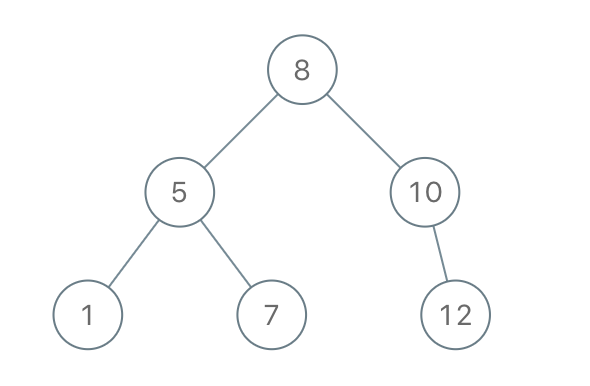
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]
Output: [1,null,3]

Constraints:

・ 1 <= preorder.length <= 100
・ 1 <= preorder[i] <= 10⁸
・ All the values of preorder are unique.

Idea

Preorder로 표현된 binary search tree만 가지고 tree를 재구성해보는 문제다. Preorder는 부모 노드부터 시작해 왼쪽, 오른쪽 자식 노드 순으로 값을 넣는다. 또한 만들어야 할 tree가 BST (binary search tree)이므로 preorder array를 순차적으로 탐색하면서 부모 노드의 값을 가지고 왼쪽에 들어갈 자식 노드들과 오른쪽에 들어갈 자식 노드들을 구분해야 한다. 그냥 순차적으로 boundary를 찾을 수도 있지만 O(n)이 걸리므로 binary search를 통해 O(nlogn)으로 찾는 것이 낫다.

Binary Search에서는 중간 index를 구한다. 해당 index가 끝값에 오거나 부모 노드의 값이 중간 index 값과 (중간 index+1) 값 사이에 올 경우 boundray를 찾은 것이다. boundray를 찾지 못 했다면, 중간 index를 시작 index나 끝 index로 바꾸어 boundary를 찾을 때까지 반복한다.

Binary Search 함수를 구현한 뒤 BST를 만들 수 있다. boundray를 찾았으면 부모 노드의 왼쪽은 부모 노드 index의 다음부터 boundary까지, 오른쪽은 boundray+1부터 끝 index까지를 인자로 줘서 재귀함수를 호출한다. 자식 노드를 모두 만들었으면 부모 노드를 리턴하면 된다.

Binary Search 구현을 너무 난잡하게 해서 좀 더 깔끔하게 할 수 있는 방법을 찾아야겠다. 어쨌든 한 번에 제대로 풀었으니 만족!

Solution

class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
    	return constructBst(preorder, 0, preorder.length-1);
    }

    private TreeNode constructBst(int[] preorder, int startIndex, int endIndex) {
        if (startIndex > endIndex)
            return null;

        TreeNode root = new TreeNode(preorder[startIndex]);
   
        int boundary = binarySearch(preorder, root.val, startIndex+1, endIndex);
   
        root.left = constructBst(preorder, startIndex+1, boundary);
        root.right = constructBst(preorder, boundary+1, endIndex);

        return root;
    }

    private int binarySearch(int[] preorder, int value, int startIndex, int endIndex) {
        int i = startIndex;
        int j = endIndex;
        int ret = 0;

        if (startIndex > endIndex)
            return endIndex;

        while (true) {
            int mid = i + (j - i)/2;
            if (mid == endIndex) {
                if (value > preorder[mid])
                    ret = mid;
                else
                    ret = mid-1;
                break;
            }
   
            if (value > preorder[mid] && value < preorder[mid+1]) {
                ret = mid;
                break;
            }
            else if (value < preorder[mid] && value < preorder[mid+1]) {
                if (mid == startIndex) {
                    ret = mid - 1;
                    break;
                }
                j = mid;
            }
            else if (value > preorder[mid] && value > preorder[mid+1]) {
                i = mid+1;
            }
        }
   
        return ret;
    }
}

Reference

https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/