[leetcode #1143] Longest Common Subsequence

Problem

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".
A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

・ 1 <= text1.length, text2.length <= 1000
・ text1 and text2 consist of only lowercase English characters.

Idea

전형적인 dp 문제다. 주어진 두 string의 common subsequence의 길이를 구해야 한다. 각 substring 끼리의 common subsequence 길이를 dp에 저장한 다음, 마지막 dp값을 리턴하면 된다.

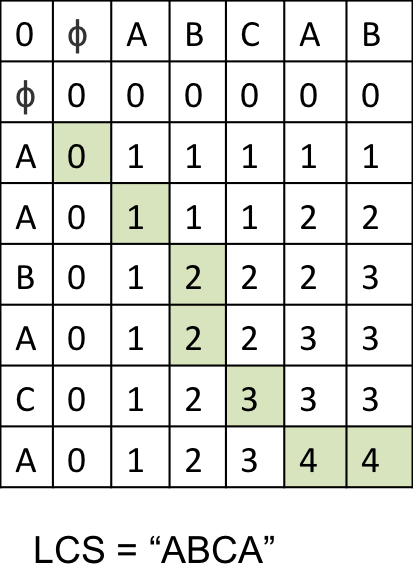
우선 행과 열이 주어진 string의 길이보다 1 더 큰 2-d array를 만든다. 이는 각 string 앞에 빈 값을 두어 다음 dp값을 구할 때 활용하기 위함이다.

각 substring을 탐색하면서 두 string의 문자가 같을 경우 현 substring의 길이가 1보다 짧은 substring 끼리의 common subsequence 길이에 1을 더하면 된다.

dp[i+1][j+1] = dp[i][j]+1

문자가 같지 않을 경우 인접한 dp값 중 큰 값을 저장한다.

dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1])

마지막으로 dp에서 가장 끝에 저장된 값을 리턴하면 된다.

Solution

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int[][] dp = new int[len1+1][len2+1];
   
        for (int i=0; i < len1; i++) {
            for (int j=0; j < len2; j++) {
                if (text1.charAt(i) == text2.charAt(j))
                    dp[i+1][j+1] = dp[i][j]+1;
                else
                    dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1]);
            }
        }

        return dp[len1][len2];
    }
}

Reference

https://leetcode.com/problems/longest-common-subsequence/