[leetcode #1217] Minimum Cost to Move Chips to The Same Position

Problem

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

・ position[i] + 2 or position[i] - 2 with cost = 0.
・ position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

Example 1:

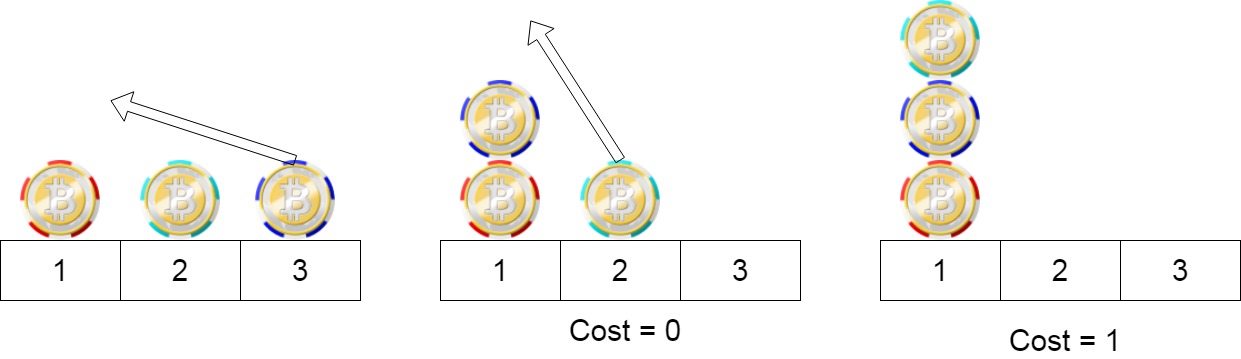
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Example 2:

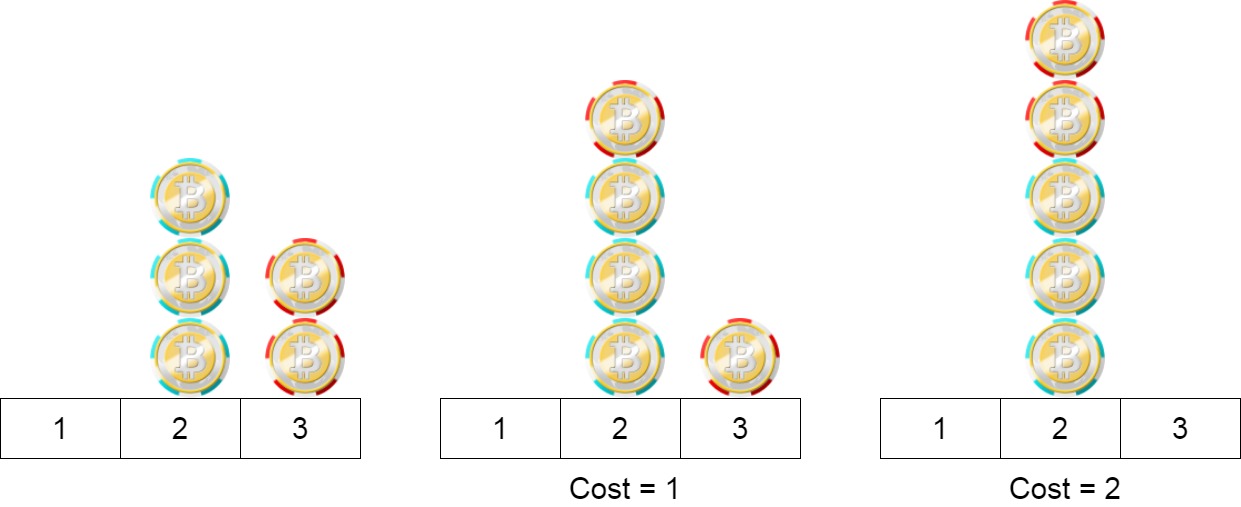
Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position  3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:

Input: position = [1,1000000000]
Output: 1

Constraints:

・ 1 <= position.length <= 100
・ 1 <= position[i] <= 10⁹

Idea

동전을 한 곳으로 모으는 최소 비용이 얼마인지 구하는 문제다.

위치가 2가 차이나는 곳으로 동전을 이동하면 비용이 들지 않지만, 1이 차이나면 비용이 1이 든다. 즉 같은 홀수이거나 짝수인 위치의 동전들을 한 곳에 모으는 건 비용이 들지 않는다. 인접한 홀수와 짝수로 동전을 모은 뒤, 더 적은 수의 동전을 홀수나 짝수로 이동시키면 최소의 비용이 발생한다. 즉, 짝수에 위치한 동전이 더 많다면 홀수에 위치한 동전의 개수를 리턴하고, 홀수에 위치한 동전이 더 많다면 짝수에 위치한 동전의 개수를 리턴하면 된다.

Solution

class Solution {
    public int minCostToMoveChips(int[] position) {
        int odd = 0;
        int even = 0;

        for (int i : position) {
            if (i % 2 == 0) {
                even++;
                continue;
            }

            odd++;
        }

        return even > odd ? odd : even;
    }
}

Reference

https://leetcode.com/problems/minimum-cost-to-move-chips-to-the-same-position/