[leetcode #1339] Maximum Product of Splitted Binary Tree

Problem

Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.

Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 10⁹ + 7.

Note that you need to maximize the answer before taking the mod and not after taking it.

Example 1:

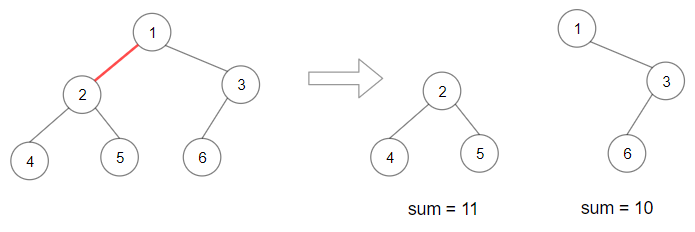
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

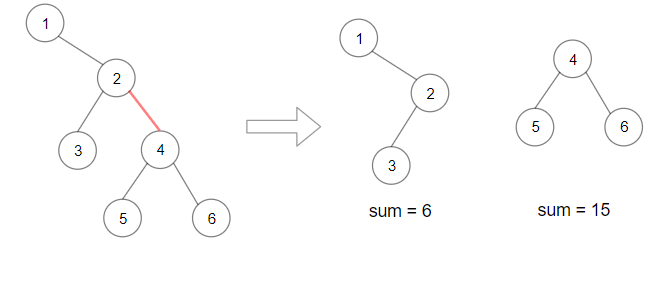
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

Constraints:

・ The number of nodes in the tree is in the range [2, 5 * 10⁴].
・ 1 <= Node.val <= 10⁴

Idea

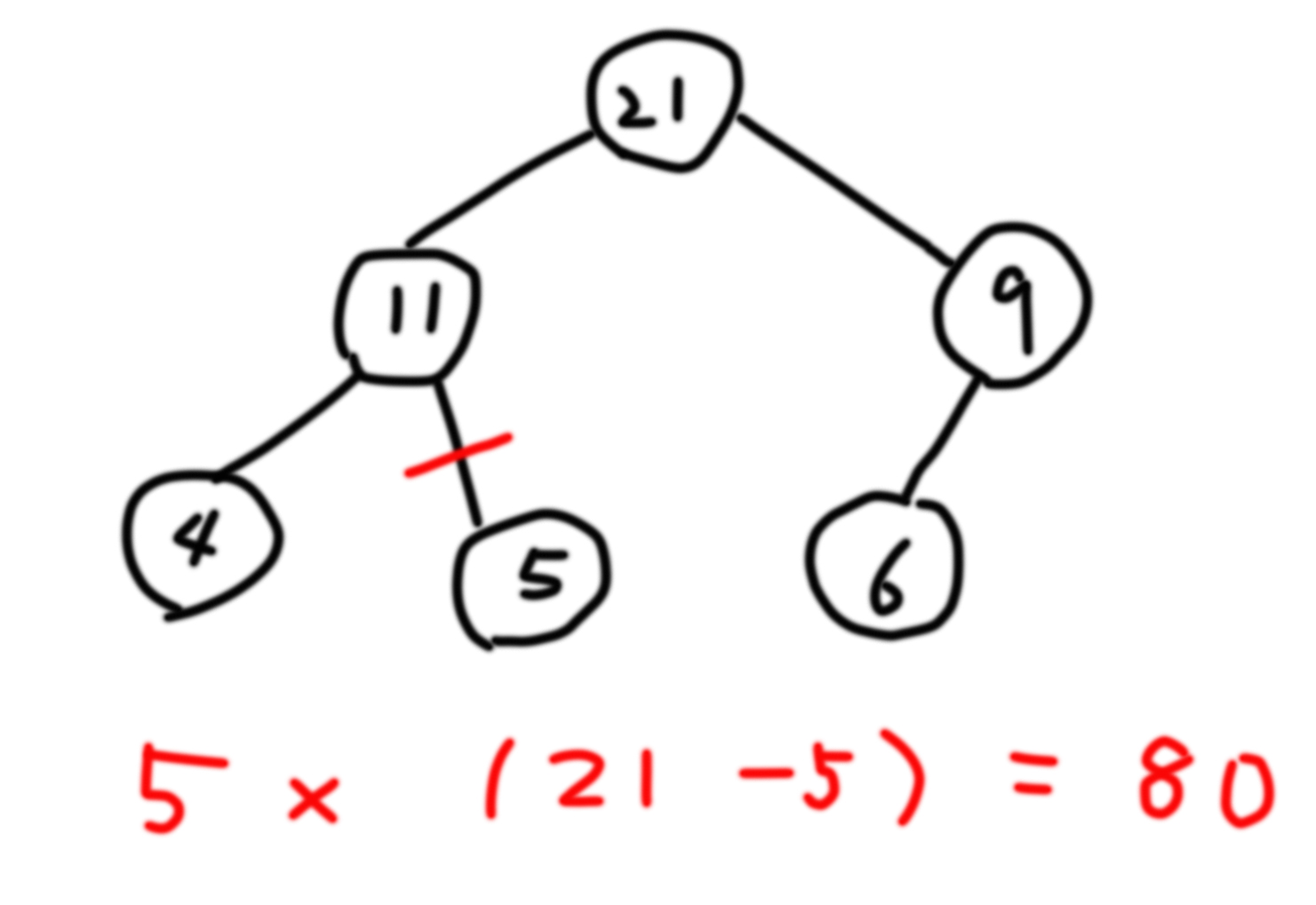
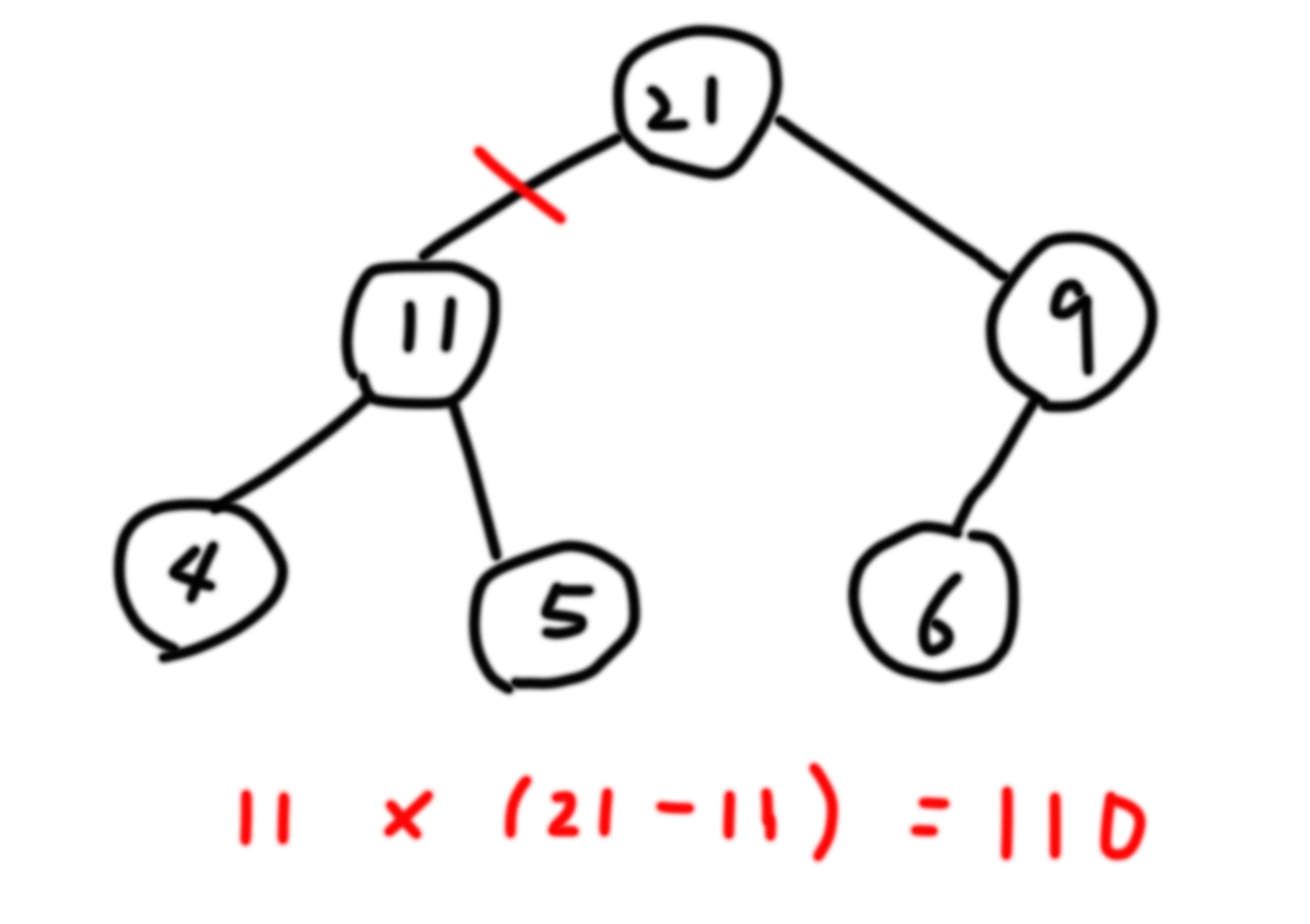
Binary Tree에서 edge를 하나 없앴을 때 나눠지는 두 tree의 합을 곱했을 때 최대값을 구하는 문제다. Edge라고 해서 Graph 관련 문제일까 걱정하지 말고 간단하게 생각하면 쉽게 풀 수 있다. 우선 각 노드의 value를 자신의 노드 값과 자식 노드의 합을 더한 값으로 설정한다. root의 값은 모든 노드의 합이 될 것이다.

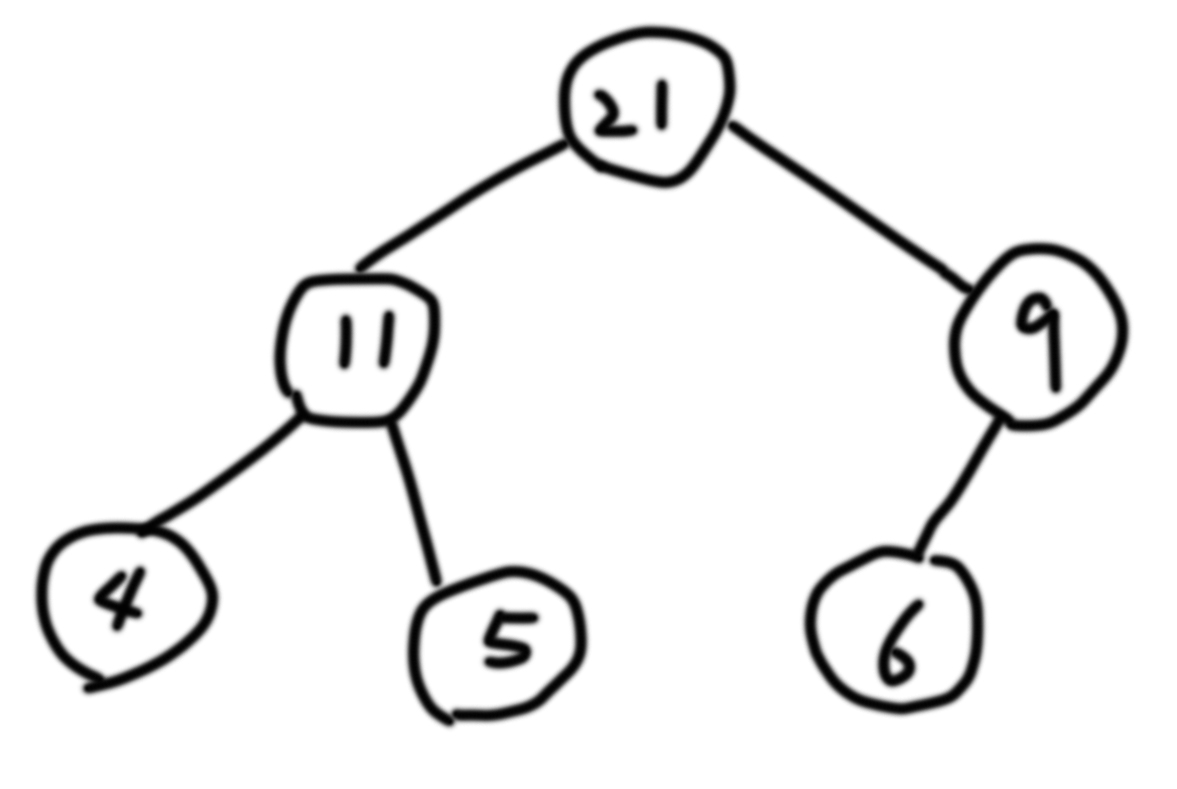
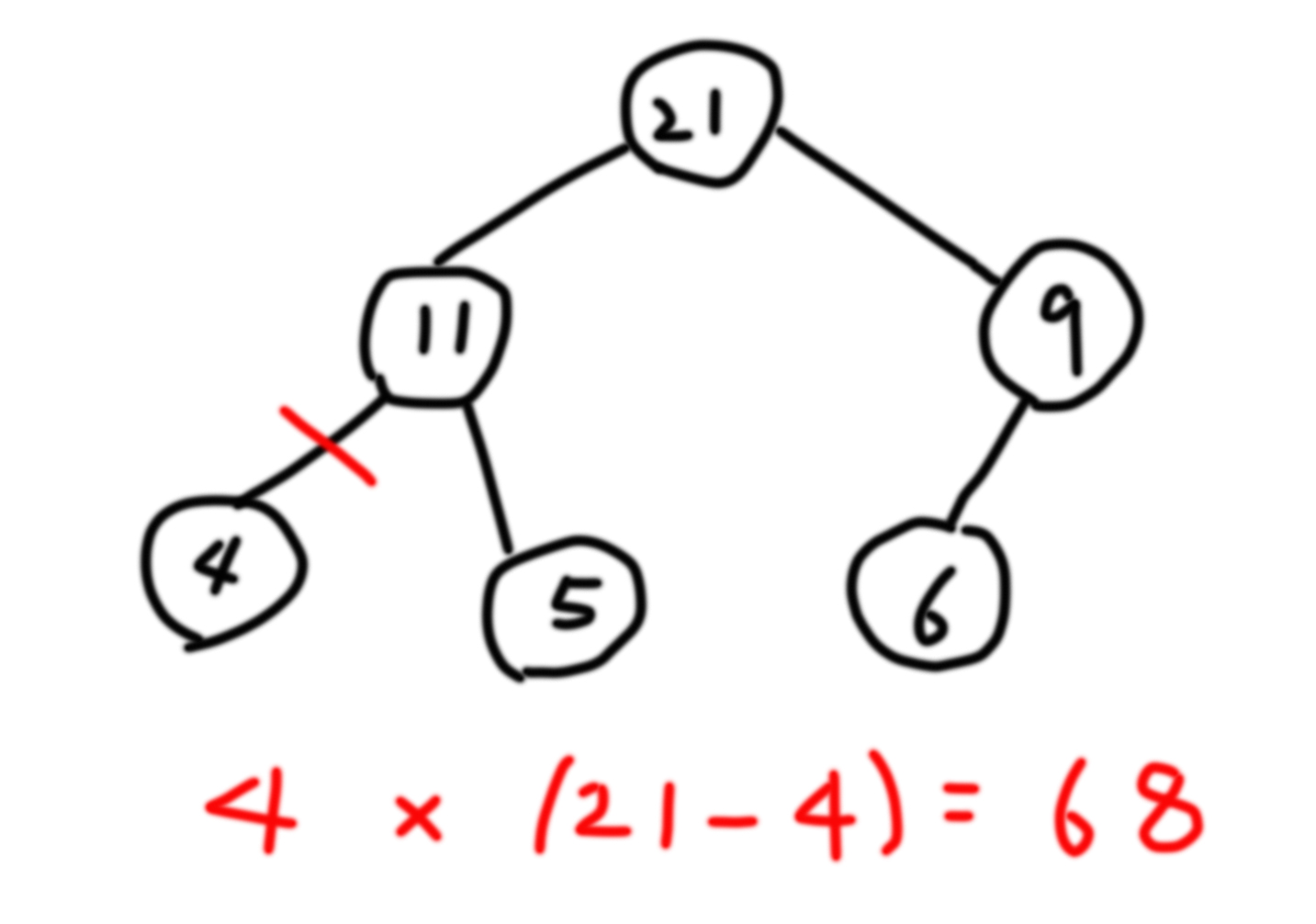
이후 tree를 재탐색하면서 해당 노드가 가지고 있는 value와 전체 노드의 합에서 해당 노드가 가지고 있는 value을 뺀 값을 곱한다. 곱한 값이 현재 최대값보다 크면 최대값을 바꾸고 모든 노드를 탐색한 후 최대값을 10⁹+7로 나눈 값을 리턴하면 된다. 이런 과정을 반복하는 이유는 곱하는 두 개의 값이 해당 노드의 위 edge를 제거했을 때 나눠지는 두 트리의 합이기 때문이다.



알고리즘은 다음과 같다.

1. 트리를 탐색하면서 각 노드의 값을 subtree의 합으로 바꿔준다.
   a. 노드가 null일 경우 0을 리턴한다.
   b. 자식 노드가 없을 경우 해당 노드의 val을 리턴한다.
   c. 자식 노드가 있을 경우 자식 노드의 val과 해당 노드의 val을 합한 값으로 val을 설정한다.
2. 트리를 재탐색하면서 maxValue를 찾는다.
   a. 노드의 값과 모든 트리의 합에서 노드의 값을 뺀 값을 곱한다. 해당 값이 maxValue보다 클 경우 maxValue를 바꿔준다.
   b. 자식 노드들을 인자로 넣어 재귀함수를 호출한다.
3. maxValue를 10⁹+7로 나눈 나머지를 리턴한다.

Solution

class Solution {
    long ans = 0;

    public int maxProduct(TreeNode root) {
	long totalSum = setTreeSum(root);

    	findMaxValue(root, totalSum);

    	return (int) (ans % 1_000_000_007);
    }

    private int setTreeSum(TreeNode node) {
        if (node == null)
            return 0;

        if (node.left == null && node.right == null)
            return node.val;

        node.val += setTreeSum(node.left) + setTreeSum(node.right);

        return node.val;
   }

    private void findMaxValue(TreeNode node, long totalSum) {
        if (node == null)
            return;

        long prod = node.val * (totalSum - node.val);
        if (prod > ans)
            ans = prod;

        findMaxValue(node.left, totalSum);
        findMaxValue(node.right, totalSum);
    }
}

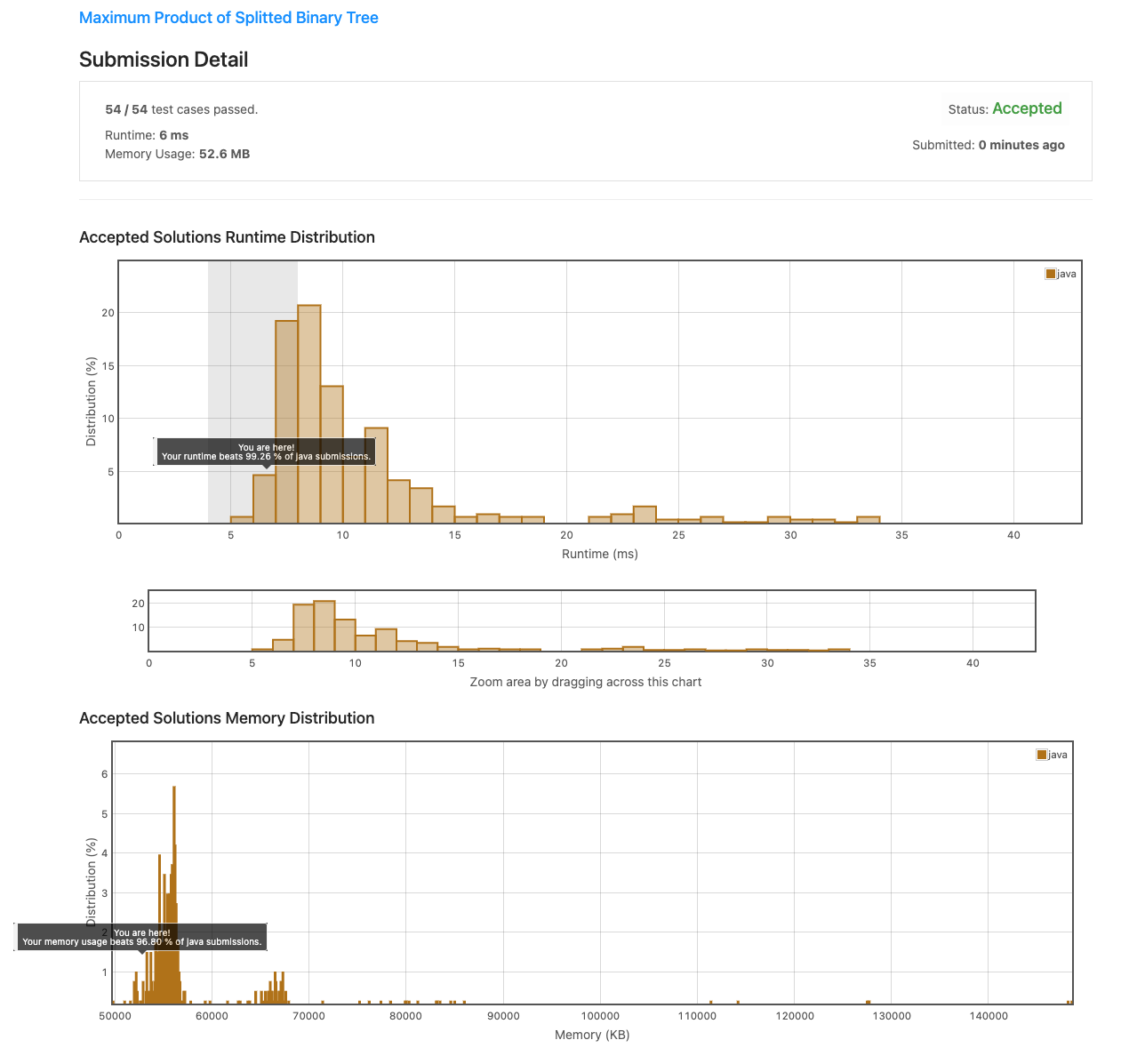
생각지도 못 했는데 Runtime, Memory 모두 훌륭한 결과를 보여주었다!

Reference

https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/