[leetcode #222] Count Complete Tree Nodes

Problem

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example 1:

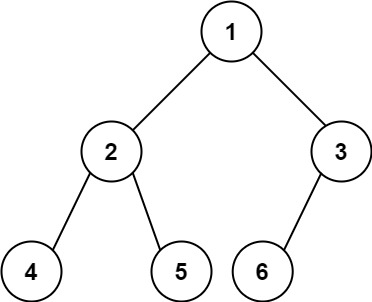
Input: root = [1,2,3,4,5,6]
Output: 6

Example 2:

Input: root = []
Output: 0

Example 3:

Input: root = [1]
Output: 1

Constraints:

・ The number of nodes in the tree is in the range [0, 5 * 10⁴].
・ 0 <= Node.val <= 5 * 10⁴
・ The tree is guaranteed to be complete.

Idea

Complete Tree의 노드 수를 세는 문제다. 그냥 단순하게 tree를 탐색하면서 노드 개수를 세면 쉽게 문제를 풀 수 있지만, complete tree이기 때문에 평균적으로 O(n)보다 적은 time complexity로 문제를 풀 수 있다. Complete Tree는 탐색하면서 왼쪽 자식 노드만 가진 노드를 찾거나, 형제 노드인데 depth가 다른 노드를 찾을 경우 즉시 노드의 개수를 구할 수 있다. 자식 노드를 탐색할 때 해당 노드에 매긴 숫자를 통해 개수를 구할 수 있는 것이다.

이렇게 풀면 결과가 좋을 것으로 생각했으나, 실제론 1ms가 걸려서 다른 사람은 어떻게 풀었는지 확인했다.

0ms가 나오는 풀이는 다음과 같다. 매번 노드를 탐색할 때 왼쪽 subtree의 depth와 오른쪽 subtree의 depth를 비교한다. 두 depth가 같을 경우 왼쪽 subtree가 full tree이므로 오른쪽 subtree를 탐색하고 왼쪽 subtree의 depth를 left shifting한 만큼의 값을 노드 개수에 더한다. depth가 다를 경우 오른쪽 subtree가 full tree이므로 왼쪽 subtree를 탐색하고 오른쪽 subtree의 depth를 right shifting한 만큼의 값을 노드 개수에 더한다. 이 과정을 반복하면 노드의 개수를 쉽게 구할 수 있다.

Solution

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null)
            return 0;
    
        return traverseTree(root, 0, 0, 1);
    }

    private int traverseTree(TreeNode node, int depth, int maxDepth, int num) {
        if (depth > maxDepth)
            maxDepth = depth;
        if (node.left == null && node.right == null) {
            if (maxDepth != depth)
                return 2 * num - 1;
            else
                return num;
        }
        if (node.left != null & node.right == null)
            return 2 * num;
    
        int left = traverseTree(node.left, depth+1, maxDepth, num*2);
        int right = traverseTree(node.right, depth+1, maxDepth, num*2+1);
    
        return Math.max(left, right);
    }
}

위 코드가 내가 짠 코드며, 아래처럼 짜는게 훨씬 낫다.

class Solution {
    public int countNodes(TreeNode root) {
        // Base case
        if(root == null) return 0;
    
        // Get the leftDepth of left subtree and right subtree to check which one is unfull tree
        int left = leftDepth(root.left);
        int right = leftDepth(root.right);
    
        if(left == right) {
            // Left subtree is a full tree, and right subtree could be a non-full tree
            return (1 << left) + countNodes(root.right);
        
        } else {
            // Right subtree is a full tree, and left subtree could be a non-full tree
            return countNodes(root.left) + (1 << right);
        }
    }

    private int leftDepth(TreeNode root) {
        int ans = 0;
    
        while(root != null) {
            ans++;
            root = root.left;
        }
    
        return ans;
    }
}

Reference

https://leetcode.com/problems/count-complete-tree-nodes/