[leetcode #337] House Robber III

Problem

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example 1:

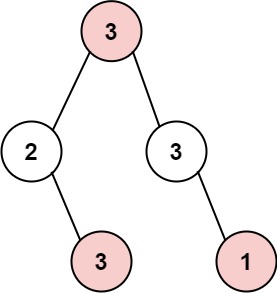
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

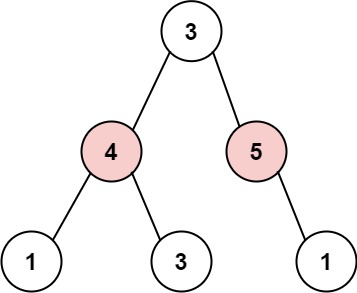
Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

Constraints:

・ The number of nodes in the tree is in the range [1, 10⁴].
・ 0 <= Node.val <= 10⁴

Idea

얼마 전에 나온 House Robber와 비슷한 문제다. 저번 문제가 집마다 들고 있는 돈의 액수가 list로 저장되었다면, 이번에는 Tree에 저장되어 있다는 점이 차이다. 이전과 동일하게 연속된 node를 동시에 털 수는 없다.

Tree라서 어렵게 생각할 필요는 없고, 알고리즘만 잘 세우면 된다. Tree기 때문에 재귀함수를 이용해서 풀기로 결심만 하면 그렇게 어렵지는 않다.

Tree를 탐색할 때는 각 노드 별로 해당 노드가 포함되었을 때 최대값과 포함되지 않았을 때 최대값을 리턴하도록 만들었다. 포함되지 않았을 경우는 index가 0, 포함되었을 경우는 index가 1이다.

node가 null일 때는 두 값 모두 0인 array를 만들어 리턴한다. null이 아닌 경우, 왼쪽 자식 노드와 오른쪽 자식 노드를 인자로 하여 재귀함수를 호출한다. 자식 노드가 가진 값들을 이용해 현재노드가 포함되었을 경우와 포함되지 않았을 경우의 최대값을 구한다.

현재 노드가 포함된 경우는 현재 노드의 값과 왼쪽 자식 노드가 포함되지 않았을 때 최대값, 오른쪽 자식 노드가 포함되지 않았을 때 최대값을 더한 값이 최대값이 된다.

현재 노드가 포함되지 않았을 경우에는 왼쪽 자식 노드의 유무와 관계없이 최대값을 구하고, 오른쪽 자식 노드의 유무와 관계없이 최대값을 구한 뒤 두 값을 더한 값이 최대값이 된다.

재귀함수에서는 두 값을 array로 만들어 리턴하고, 처음 호출할 때 루트 노드를 인자로 해서 넣어주면 빈집털이를 통해 얻을 수 있는 액수의 최대값을 알 수 있다.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        int[] rootValue = traverse(root);

        return Math.max(rootValue[0], rootValue[1]);
    }

    private int[] traverse(TreeNode node) {
        if (node == null) {
            return new int[2];
        }

        int[] left = traverse(node.left);
        int[] right = traverse(node.right);
        int selfIncluded = node.val + left[0] + right[0];
        int selfNotIncluded = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);

        return new int[] {selfNotIncluded, selfIncluded};
    }
}

Reference

https://leetcode.com/problems/house-robber-iii/