[leetcode #790] Domino and Tromino Tiling

Problem

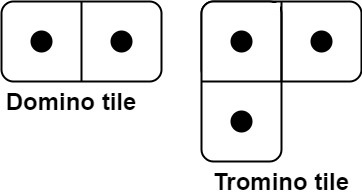
You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

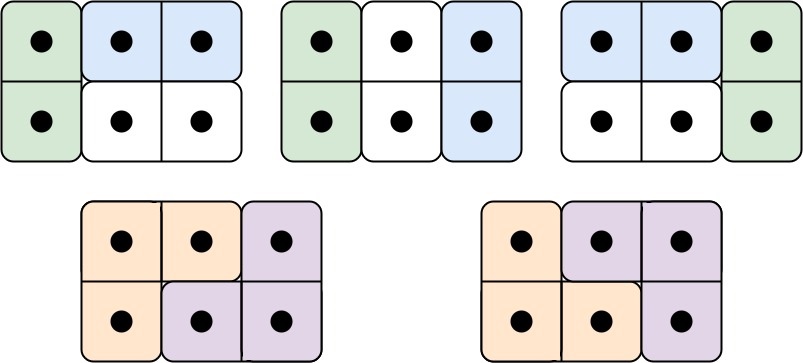
Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

・ 1 <= n <= 1000

Idea

너무나 흥미로운 문제다. 주어진 두 종류의 도미노를 사용하여 2xn 보드를 만들 때 가능한 경우가 몇 가지인지 구하면 된다.

당연히 dp로 풀면 될 것으로 생각하고 dp를 어떻게 설계하면 될 지 고민했다.

우선 가로 길이를 기준으로 가능한 수를 생각했다.
1. 너비가 1일 때 가능한 경우는 Domino tile을 세로로 세우는 것 한 가지다. dp(1) = 1
2. 너비가 2일 때 가능한 경우는 Domino tile 두 개를 세로 또는 가로로 나열하는 것이다. dp(2) = 2
3. 너비가 3일 때 가능한 경우는 Domino tile을 세로로 세운 뒤 2번에서 만든 보드를 붙이는 것, Domino tile 두개를 가로로 만든 뒤 1번에서 만든 보드를 붙이는 것, 그리고 Tromino tile 두개를 이어서 만드는 것이 있다. dp(2) = 2 + 1 + 2

n = 4 부터는 Tromino tile과 Domino tile을 이용해 앞에서 계산한 dp를 이용하지 않는 방법이 2가지가 무조건 존재한다. 따라서 dp 수식을 만들면 다음과 같다.

dp[4] = dp[1] x 2 (Tromino tile을 이용해 너비 3인 보드 만드는 법) + dp[2] + dp[3] + 2 (앞에서 만든 보드를 사용하지 않고 너비 4인 보드를 만드는 법)
dp[5] = (dp[1] + dp[2]) x 2 + dp[3] + dp[4]

위와 같은 수식이 나오는 이유는 너비가 3 이상일 때 앞에서 만든 타일을 이용하지 않는 고유의 방법이 2가지가 있기 때문이다.

위 수식을 이용하면 O(N²)이 나온다. 통과는 하지만 다른 풀이보다 오래 걸려서 리트코드의 풀이를 봤다.

leetcode의 알고리즘은 다음과 같다.

1. Create two arrays, ff and pp, of size n+1n+1, where f(k)f(k) represents the number of ways to fully cover a board of width kk and p(k)p(k) represents the number of ways to partially cover a board of width kk (as described in the overview).
2. Initialize ff and pp according to the following base cases:
   ・ f(1) = 1f(1)=1 because to fully cover a board of width 1, there is only one way, add one vertical domino.
   ・ f(2) = 2f(2)=2 because to fully cover a board of width 2, there are two ways, either add two horizontal dominos or add two vertical dominos.
   ・ p(2) = 1p(2)=1 because to partially cover a board of width 2, there is only one way using an L-shaped tromino (leave the upper-right corner uncovered).
3. Iterate kk from 22 to nn (inclusive) and at each iteration update ff and pp according to the transition functions we derived in the overview:
   ・ f(k) = f(k-1) + f(k-2) + 2 * p(k-1)f(k)=f(k−1)+f(k−2)+2∗p(k−1)
   ・ p(k) = p(k-1) + f(k-2)p(k)=p(k−1)+f(k−2)
4. Return f(n)f(n) which now represents the number of ways to fully cover a board of width nn.

Partial 보드를 계산하여 수식을 세우면 O(N)으로 풀 수가 있다! 원문을 보면 쉽게 이해할 수 있으므로 꼭 읽어보기를...

Solution

class Solution {
    public int numTilings(int n) {
        long[] dp = new long[Math.max(n+1,4)];
        dp[1] = 1;
        dp[2] = 1 + 1;

        for (int i=3; i <= n; i++) {
            for (int j=1; j < i; j++) {
                if (j == 1 || j == 2) {
                    dp[i] += dp[i-j];
                } else {
                    dp[i] += 2 * dp[i-j];
                }
            }
            dp[i] += 2;
            dp[i] %= 1_000_000_007;
        }

        return (int) (dp[n] % 1_000_000_007);
    }
}

아래는 leetcode solution이다.

class Solution {
    public int numTilings(int n) {
        int MOD = 1_000_000_007;
        // handle base case scenarios
        if (n <= 2) {  
            return n;
        }
        // f[k]: number of ways to "fully cover a board" of width k
        long[] f = new long[n + 1];  
        // p[k]: number of ways to "partially cover a board" of width k
        long[] p = new long[n + 1];  
        // initialize f and p with results for the base case scenarios
        f[1] = 1L;
        f[2] = 2L;
        p[2] = 1L;
        for (int k = 3; k < n + 1; ++k) {
            f[k] = (f[k - 1] + f[k - 2] + 2 * p[k - 1]) % MOD;
            p[k] = (p[k - 1] + f[k - 2]) % MOD;
        }
        return (int) (f[n]);
    }
}

Reference

https://leetcode.com/problems/domino-and-tromino-tiling/