[leetcode #797] All Paths From Source to Target

Problem

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:

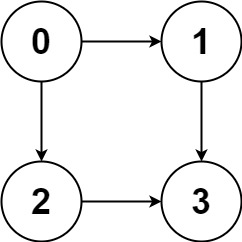
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

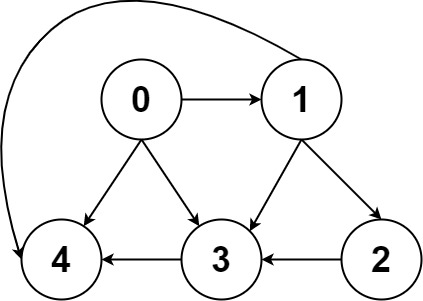
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Example 3:

Input: graph = [[1],[]]
Output: [[0,1]]

Example 4:

Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]

Example 5:

Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]

Constraints:

・ n == graph.length
・ 2 <= n <= 15
・ 0 <= graph[i][j] < n
・ graph[i][j] != i (i.e., there will be no self-loops).
・ All the elements of graph[i] are unique.
・ The input graph is guaranteed to be a DAG.

Idea

전형적인 DFS & backtracking 문제다.

DFS를 생각하기 귀찮아 처음에 map을 생성하고 graph를 돌면서 node를 key로, 해당 node로 향하는 node들의 리스트를 value로 만들었다.

이후엔 (n-1)인 노드를 첫 인자로 주고 backtracking을 시작한다. map을 통해 해당 노드로 향하는 노드의 리스트를 얻은 뒤, 리스트에 노드를 더하고 바뀐 노드를 backtracking의 인자로 넣어 리스트의 첫번째 값이 0이 나올 때까지 진행한다.

backtracking이 끝나면 리턴할 리스트에는 (n-1) node로 향하는 노드들의 리스트가 전부 들어있게 된다.

★ map을 안 쓰고 DFS로 푸는 방법이 있으므로 참고하세요!

Solution

class Solution {
    List<List<Integer>> res;
    Map<Integer, List<Integer>> map;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        map = new HashMap<>();

        for (int i=0; i < graph.length; i++) {
            int[] points = graph[i];
            for (int point : points) {
                if (!map.containsKey(point))
                    map.put(point, new ArrayList<>());
                map.get(point).add(i);
            } 
        }

        res = new ArrayList<>();
        List<Integer> initialList = new ArrayList<>();
        initialList.add(graph.length-1);
        backtracking(graph.length-1, initialList);

        return res;
    }

    private void backtracking(int node, List<Integer> list) {
        if (list.get(0) == 0) {
            res.add(list);    
            return;
        }

        List<Integer> backtracked = map.get(node);

        if (backtracked == null)
            return;

        for (int current : backtracked) {
            List<Integer> newList = new ArrayList<>(list);
            newList.add(0, current);
            backtracking(current, newList);
        }

        return;
    }
}

Reference

https://leetcode.com/problems/all-paths-from-source-to-target/