[leetcode #897] Increasing Order Search Tree

Problem

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

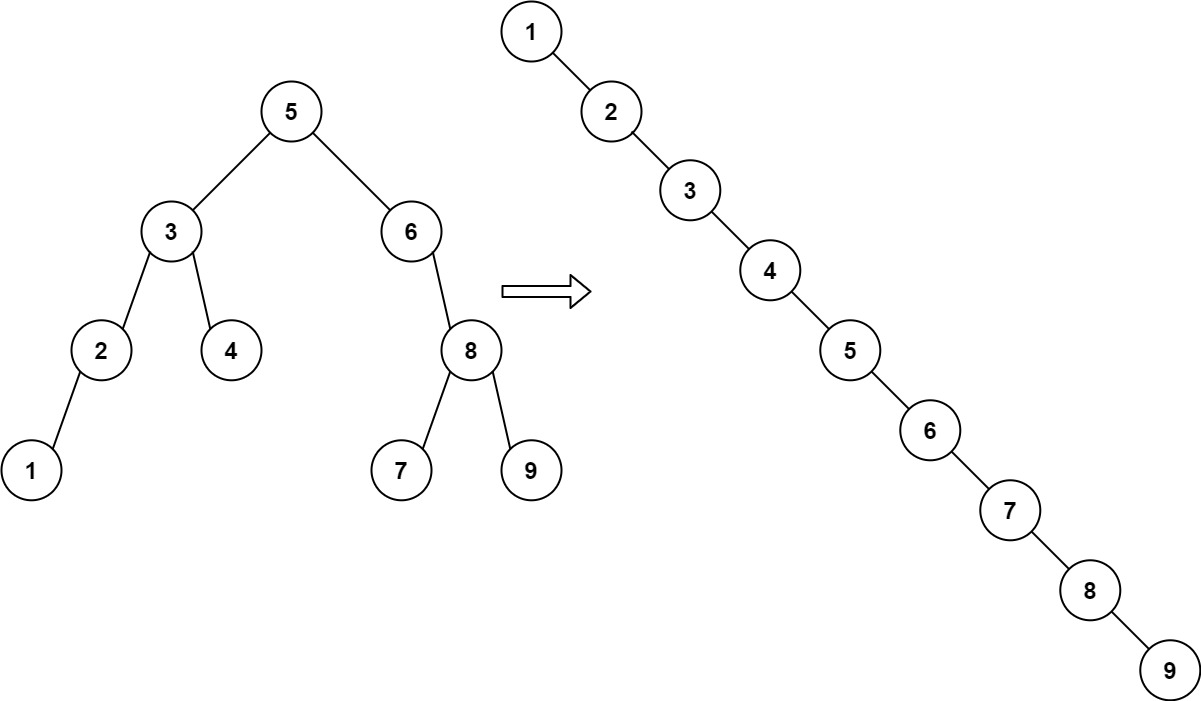
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

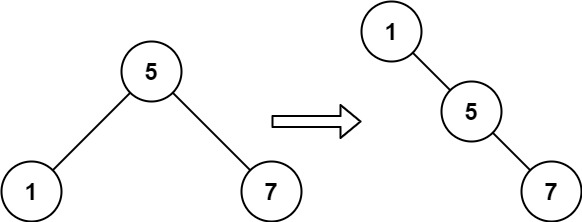
Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

· The number of nodes in the given tree will be in the range [1, 100].
· 0 <= Node.val <= 1000

Idea

주어진 BST를 왼쪽에 있는 노드 순서대로 재배열하라는 문제다. 재배열되는 트리는 왼쪽 자식 노드 없이 오른쪽 자식 노드만 가지도록 한다.

왼쪽 노드부터 순서대로 배열해야 하므로 BST를 inorder로 탐색한다. inorder로 탐색하면서 리스트에 노드를 추가하고 inorder 탐색이 끝난 뒤 리스트 순서대로 트리를 만들면 된다.

list 없이 inorder 탐색하면서 트리를 만드는 방법도 있으니 생각해보면 좋을 듯!

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<TreeNode> list = new ArrayList<>();

    public TreeNode increasingBST(TreeNode root) {
        traverseBST(root);

        TreeNode res = list.remove(0);
        res.left = null;
        res.right = null;
        TreeNode cur = res;

        while (!list.isEmpty()) {
            TreeNode node = list.remove(0);
            node.left = null;
            node.right = null;
            cur.right = node;
            cur = node;
        }

        return res;
    }

    private void traverseBST(TreeNode node) {
        if (node == null) {
            return;
        }

        traverseBST(node.left);
        list.add(node);
        traverseBST(node.right);
    }
}

Reference

https://leetcode.com/problems/increasing-order-search-tree/