알고리즘 문제를 풀다보면 구간에 대한 합을 구할 일이 많아진다.

이러 상황에 "누적 합" 이라는 방법을 통해 효율적으로 시간을 줄여보자!

알고리즘 전

아주 간단한 문제이다.

• arr[1] + arr[2] + arr[3] + arr[4] = (-2) + 3 + (-4) + 5 = 2

값들을 하나하나 다 더해주면 된다.
이때 시간복잡도는 O(N)이 나온다.

이렇게 짧고 간단한 문제라면 이와 같은 방법도 훌륭하다.
하지만, 배열의 길이가 100,000이고, 구간 합을 100,000번 구해야 한다면, 일반적인 1초를 훌쩍 넘겨 버릴 것이다.

알고리즘 사용 후

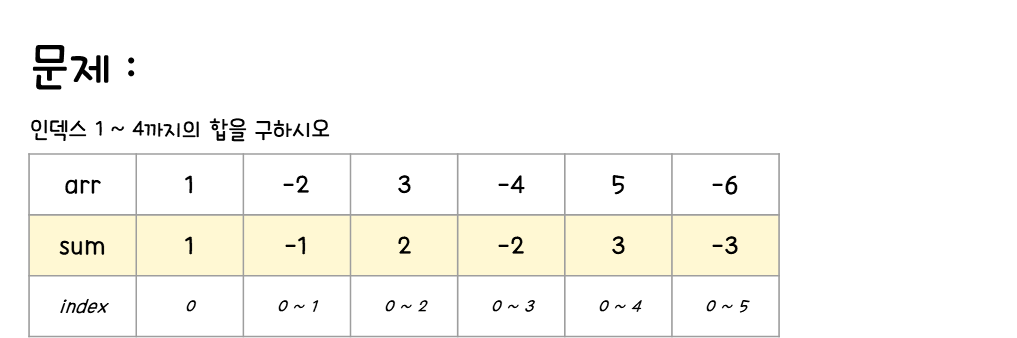
sum이라는 변수를 하나 생성하여 이 부분에 구간의 합을 삽입 할 것이다.

sum[0]에는 인덱스 0만, sum[1]에는 0~1, sum[2]에는 0~2 ... sum[i]에는 0~i까지의 합이 들어간다.

위의 문제와 같이 1부터 4까지의 합을 누적합으로 구한다면 더욱 빨라진다.

• sum[4] - sum[0] = 3 - 1 = 2

0 ~ 5 중에 우리가 구하고자 하는 정답이 1 ~ 4 이므로, 그중 0 인 sum[0]을 뺴주면 되는 것이다.
이를 통해 시간 복잡도는 O(1)이 된다.

물론 sum 배열을 제작하는 과정에서 O(N)만큼의 시간이 걸리게 된다.

하지만, 구간합을 많이 반복해야 되는 상황에서 만큼은 O(1)인 만큼 효율적이라 볼 수 있다.

실습

백준 알고리즘에서 나온 슈퍼마리오라는 문제이다.
(https://www.acmicpc.net/problem/2851)

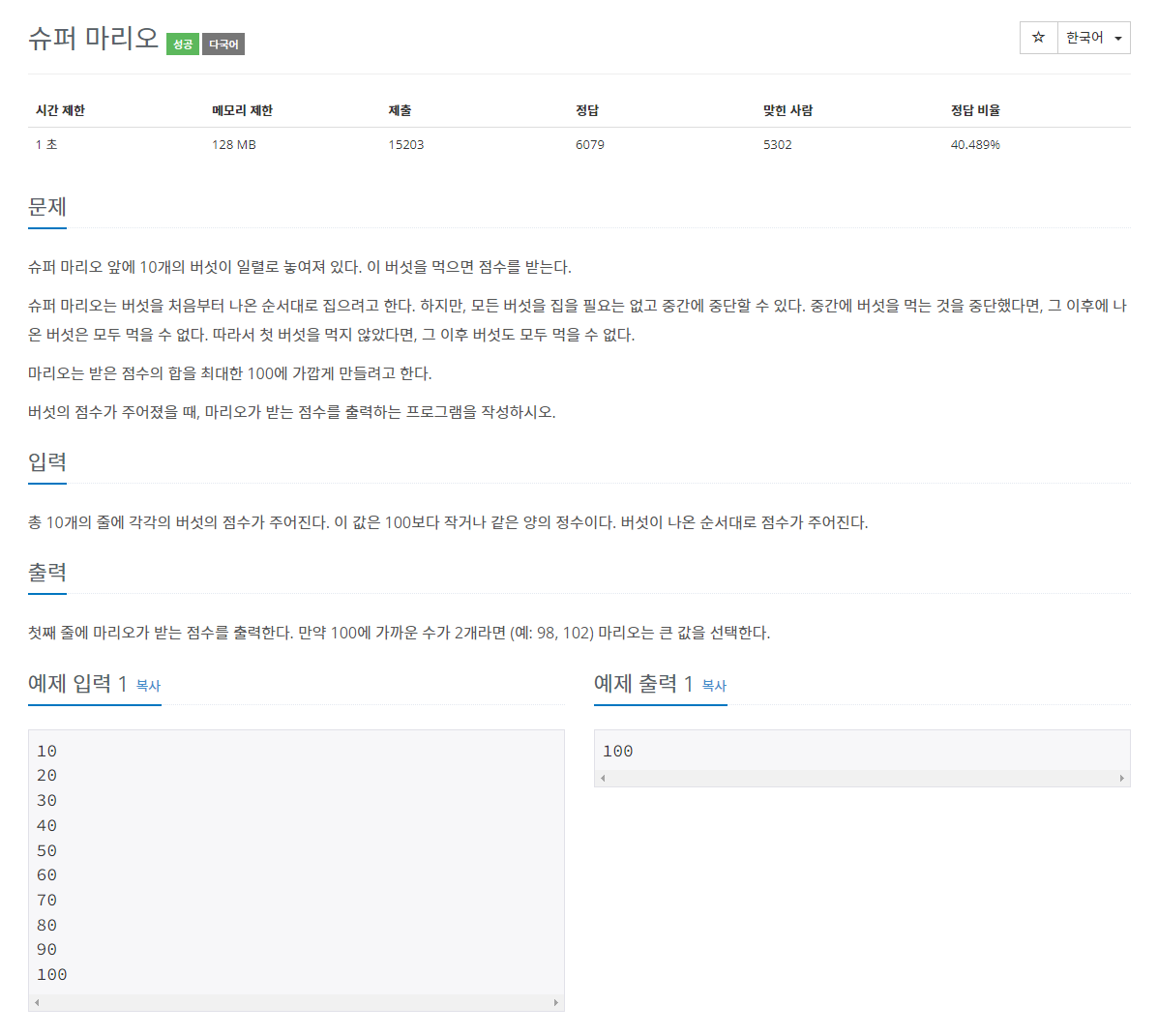
위의 문제는 아래와 같이 누적합을 이용하지 않아도 풀 수 있는 문제이다.

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = 10;
        int[] arr = new int[N + 1];

        // init
        for(int i = 1; i <= N; i++){
            arr[i] = Integer.parseInt(br.readLine());
        }

        int result = 0;

        for(int i = 1; i <= N; i++){
            int sum = 0;
            for(int j = 1; j <= i; j++) sum += arr[j];

            int tmpNum = Math.abs(sum - 100);
            int tmpResult = Math.abs(result - 100);

            // result 보다 100과의 거리가 멀다면 다음으로
            if(tmpResult < tmpNum ) continue;

            result = sum;
        }
        List<Integer> a = new ArrayList<>();
        System.out.println(result);
    }
}

이번엔 누적합을 이용하여 풀어보겠다.

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = 10;
        int[] arr = new int[N + 1];
        int[] sum = new int[N + 1]; // 새로운 배열 생성

        // init
        for(int i = 1; i <= N; i++){
            arr[i] = Integer.parseInt(br.readLine());
            sum[i] = sum[i - 1] + arr[i]; // 누적합 배열을 초기화 시켜준다.
        }

        int result = 0;
        
        for(int num : sum){
            int tmpNum = Math.abs(num - 100);
            int tmpResult = Math.abs(result - 100);

            // result 보다 100과의 거리가 멀다면 다음으로
            if(tmpResult < tmpNum ) continue;

            result = num;
        }

        System.out.println(result);
    }
}

이 문제의 배열 크기가 10이라 많은 차이가 나지는 않지만, 메모리 양이 조금 늘은 대신, 시간이 조금 줄었다는 것을 볼 수 있다