-
MST
Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소가 되는 트리
네트워크(가중치를 간선에 할당한 그래프)에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것
-
Spanning Tree
그래프 내의 모든 정점을 포함하는 트리
n개의 정점을 n - 1개의 간선으로 연결
대표적인 예
- Prim's algo
- Kruskal's algo
두 알고리즘간의 공통점 및 차이
- 탐욕 알고리즘이 기초
- Prim's algorithm은 특정 정점에서 시작하여 해당 정점에 연결된 가장 작은 가중치의 간선을 선택 후 해당 간선으로 연결된 정점의 간선을 포함한 후 그 중 가장 작은 가중치의 간선을 선택하는 방식으로 진행
- Kruskal's algorithm은 모든 간선 중 가장 작은 가중치의 간선을 선택해가는 방식으로 진행
MST 사용 예시
- 통신망, 도로망, 유통망에서의 길이, 구축 비용, 전송 시간 등을 최소로 연결
1. 프림 알고리즘 (Prim's algorithm)
-
임의의 정점 선택 후
linked_node_list에append -
1에서 선택한 정점과 연결된 간선들을
edge_list에append -
edge_list에서 최소 가중치를 가지는 간선부터pop- 해당 간선과 연결된 정점이
linked_node_list에 들어있다면continue- 무한루프 방지
- 해당 간선과 연결된 정점이
linked_node_list에 들어있지 않다면 해당 간선을 선택 후 간선 정보를MST에append
- 해당 간선과 연결된 정점이
-
edge_list에 간선이 없을 때까지 3번을 반복
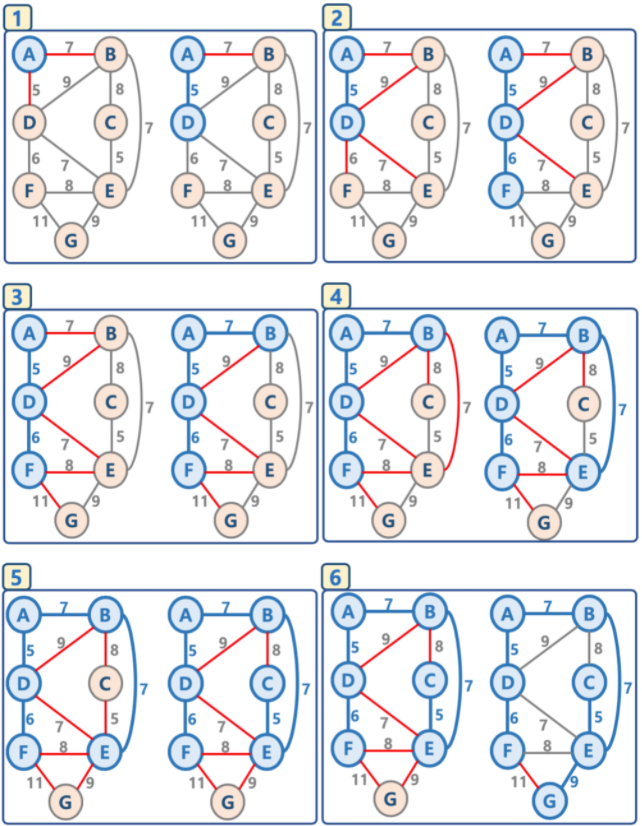
2. 크루스칼 알고리즘 (Kruskal's algorithm)
- 모든 정점을 독립적인 집합으로 생성
- 간선의 비용을 기준으로 정렬
- 가장 작은 비용의 간선을 선택 후 두 정점을 연결
- union-find 알고리즘 기준
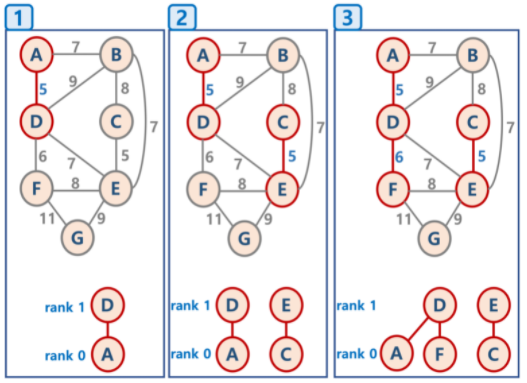
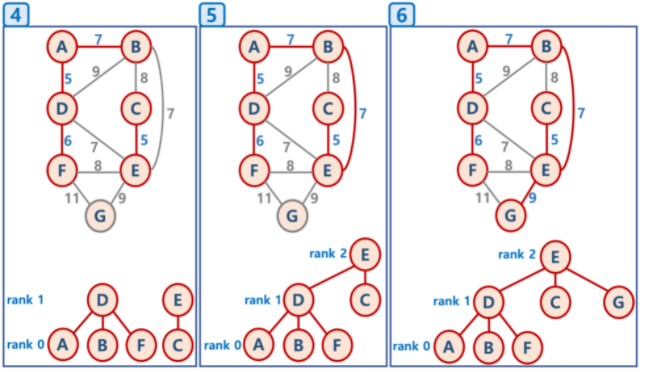
Union-Find 알고리즘
Disjoint Set을 표현할 때 사용하는 트리 구조를 활용한 알고리즘
서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
-
Union
두 개의 트리를 하나의 트리로 합친다
-
만약 두 트리의 높이가 다르면 높이가 큰 트리에 높이가 작은 트리를 붙인다
-
두 트리의 높이가 같다면 한 쪽의 트리 높이를 증가시켜준 뒤 트리를 합친다
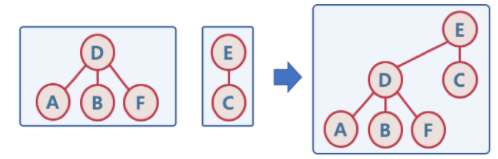
-
Find
여러 노드가 존재할 때, 두 개의 노드를 선택 후 각 노드의 루트 노드를 확인하여 서로 같은 그래프에 속하는지 판별
-
path compression
Find를 실행한 노드를 루트 노드에 다이렉트로 연결하는 기법


제가 찾던 최소신장트리 여기있네요