Day-2

1장 컴퓨터 내부의 언어 체계

4. 실수를 표현하는 방법

• 고정소수점 표현법
• 부동소수점 표현법

4-1 고정소수점 표현법

• 2비트는 2진 소수점의 오른쪽에 있는 분수들을 표현하는데 쓰고
• 2비트는 왼쪽에 있는 숫자들을 표현하는데 쓸 수 있다
• 소수점의 위치가 항상 일정하기 때문에 이런 방식을 고정소수점 표현법이라고 부른다

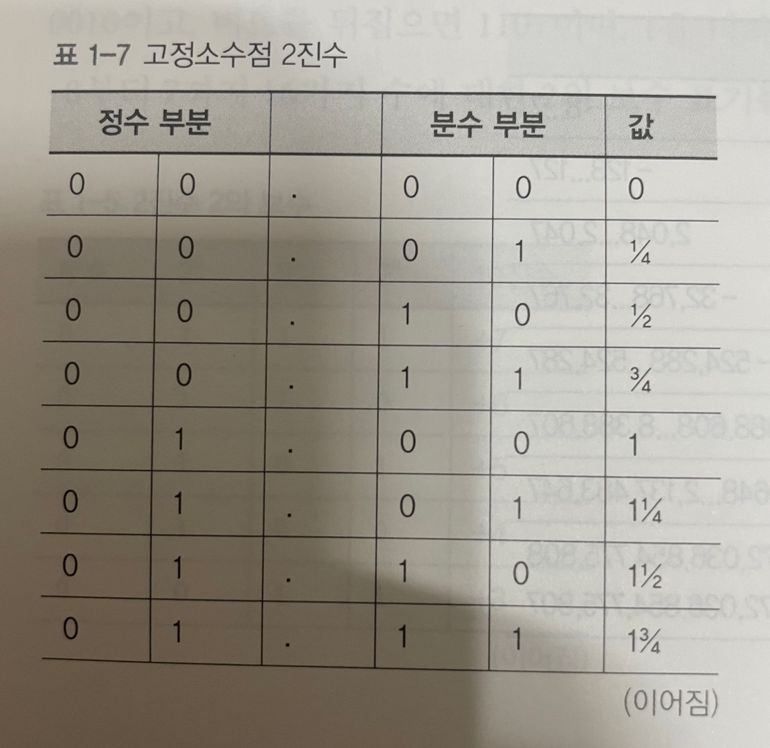
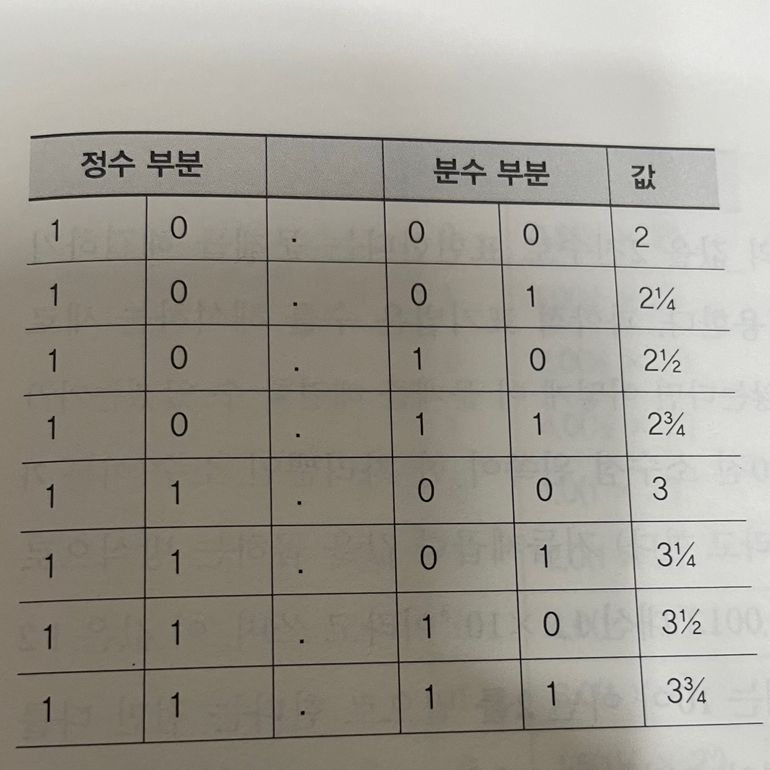
정수와 비슷하게 소수점 왼쪽의 2비트는 네 가지 정수를 표현합니다. 그리고 소수점 오른쪽의 2비트로도 네 가지 값을 표현할 수 있습니다.

2진 소수점 오른쪽에 있는 숫자들은 10진 소수점의 오른쪽에 있는 숫자들과 비슷하게 분수를 표현합니다

10진 소수와 2진수의 차이점:

• 10진 소수: 1/10, 1/100 등 10의 거듭제곱을 분모로 사용함
• 2진수: 1/2, 1/4 등 2의 거듭제곱을 분모로 사용함

범용 컴퓨터에서는 고정소수점 표현법 방식을 사용하는 경우가 드물다

왜?

• 잘 작동하기는 하지만, 쓸모 있는 범위의 실숫값을 표현하기 위해 필요한 비트 개수가 너무 많음
• 하지만 디지털 신호 처리 장치 등 특별한 목적에 쓰이는 일부 컴퓨터는 여전히 고정소수점 표현 방식을 쓰기도함

4-2 부동소수점 표현법

• 10진 소수점 왼쪽이 한 자리뿐인 소수에 10을 몇 번 거듭제곱한 값을 곱하는 방식으로 소수를 표현
• 예를들어 0.0012대신 1.2 x 10-3 이라고 쓰며, 이 값은 1.2 x 0.001 이므로 0.0012와 같다
• 가수 부분은 (소수점 왼쪽이 한 자리 뿐인) 2진 소수
• 지수 부분은 2의 거듭제곱 횟수를 표현

단순히 가수 부분만 보면 항상 2진(or 10진) 소수점의 위치가 같아보이는데,

이러한 표현 방법을 왜 부동소수점 표현법이라고 부를까?

• 가수가 1.2로 같다고 해도 지수가 무엇인가에 따라 소수점 왼 쪽 숫자의 자리가 1/10 일 수도 있고
• 1일 수도 있고, 100,000일 수도 있다는 점을 생각하면 소수점 위치는 정해져 있지 않기 때문이다

부동소수점 수의 정의상 밑 2는 항상 정해져 있다.

이러한 표현법은 지수와 가수를 분리함으로써 수를 표현할 때 필요한 0을 모두 저장하지 않고도 큰 수나 작은수를 표현할 수 있다

아래의 표는 2비트 가수와 2비트 지수를 사용하는 4비트 부동소수점 수 표현을 나타낸 표이다.

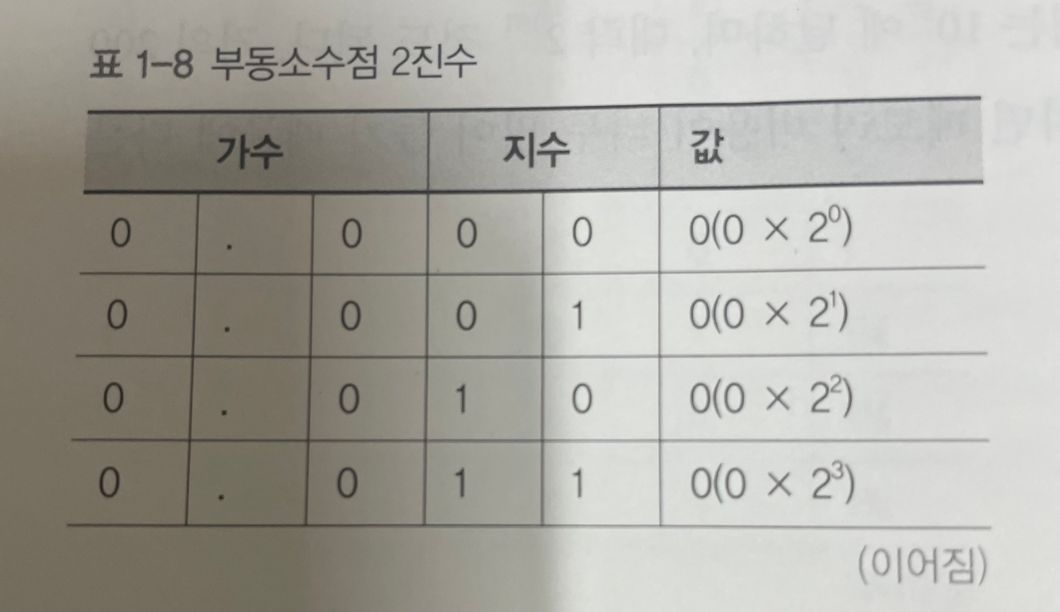
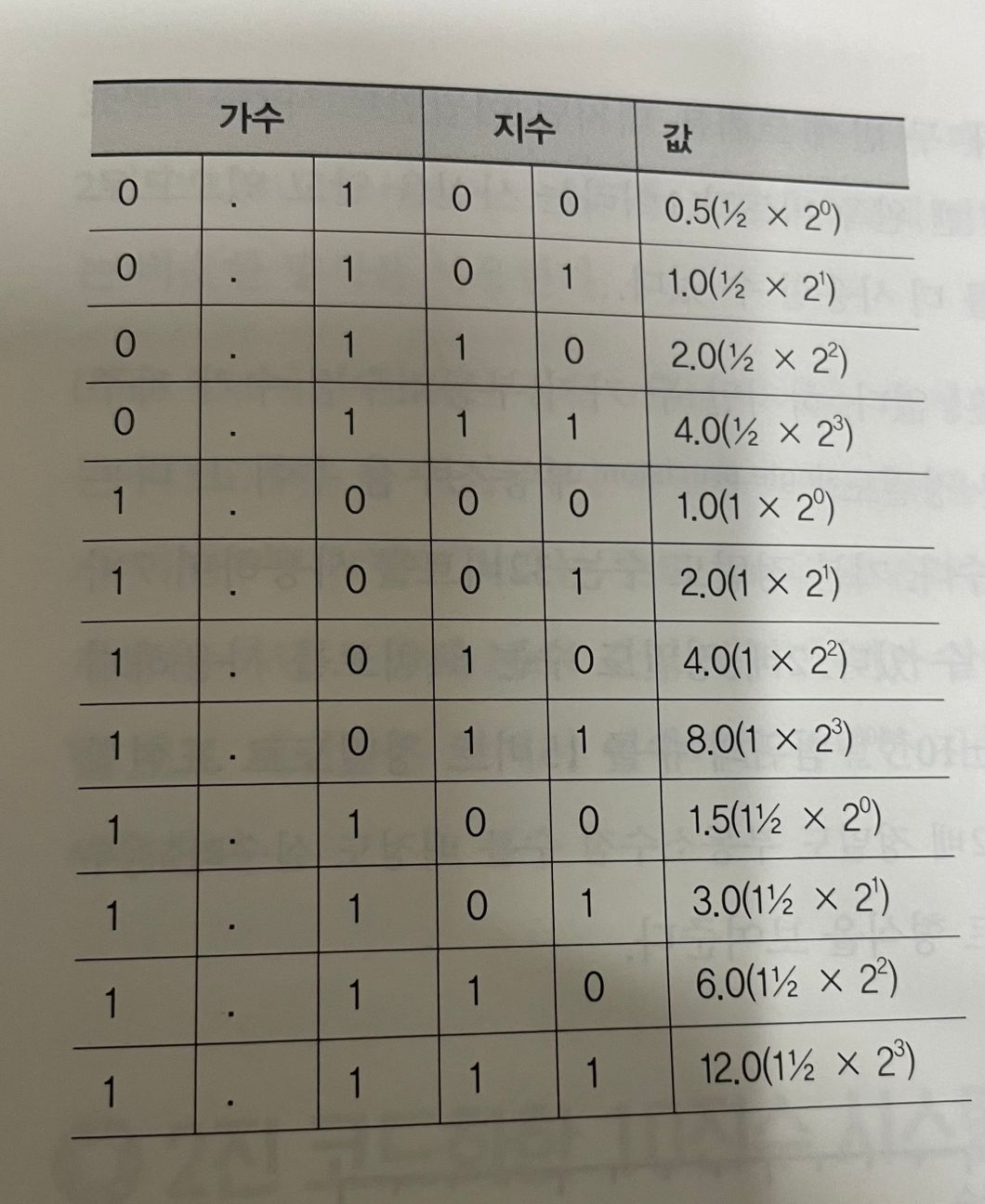
단순히 4비트만 사용하지만 부동소수점 표현법의 비효율성을 보여준다.

1. 비트 조합중에 낭비되는 부분이 많다
   • 0을 표현하는 방법은 네 가지나 되고, 1.0, 2.0, 4.0을 표현하는 방법도 두 가지씩 있다
2. 비트 패턴이 가능한 모든 수를 표현하지는 못한다
   • 지수가 커질수록 가수의 한 패턴과 다른 패턴 사이의 값 차이가 커진다
   • 0.5와 0.5를 더하면 1.0을 얻을 수 있지만 6.5를 표현하는 비트 패턴이 없기 때문에 0.5와 6.0을 더할 수는 없다는 부작용이 생김

IEEE 부동소수점 수 표준

IEEE 754 표준?

• 부동소수점 수 시스템은 컴퓨터에서 계산을 수행할 때 실수를 표현하는 표준 방법
• 위의 표보다 더 많은 비트를 사용하며, 가수와 지수에 대해 각각 부호 비트를 사용
• 다만 지수에 대한 부호 비트는 지수의 비트 패턴에 감춰져 있음
• 낭비되는 비트 조합을 최소화하고 반올림을 쉽게 하기 위한 여러가지 트릭이 사용됨

IEEE 란?

• 미국 전자전기공학회의 약자로 표준 제정 등 다양한 활동을 하는 전문가 조직

똑같은 비트를 사용하더라도 정밀도를 가능한 한 높이고 싶다면?

1. 정규화
   1. 가수를 조정해서 맨 앞 (즉, 왼쪽)에 0이 없게 만드는 것 (이런식으로 가수를 조정하려면 지수도 조정해야함)
2. 가수의 맨 왼쪽 비트가 1이라는 사실을 알고 있으므로 이를 생략하는 것
   1. 디지털 이큅먼트 사에서 고안한 것.
   2. 가수에 1비트를 더 사용할 수 있음

자주 쓰이는 두 가지 부동소수점 수

1. 기본 정밀도 부동소수점 수
   1. 32비트를 사용하며 7비트 정밀도로 대략 +- 10 +-38 정도의 범위를 표현할 수 있음
2. 2배 정밀도 부동소수점 수
   1. 64비트를 사용하기 때문에 더 넓은 범위를 표현할 수 있음.
   2. 대략 +-10 +-308 범위의 수를 15비트 정밀도로 표현할 수 있음

• 2배 정밀도 수가 기본 정밀도 수보다 지수가 3비트 더 크다는 점을 볼 수 있다.
• 지수의 범위는 8배 더 크다
• 2배 정밀도 수는 기본 정밀도 수보다 가수가 29비트 더 크다. 따라서 정밀도도 훨씬 더 크다
• 하지만 이런 모든 장점은 비트를 2배나 더 많이 사용한다는 비용을 지불하고 얻은 것

편향된 지숫값?

• 기본 정밀도의 경우 편향값은 127
• 이 말은 127(01111111)이 지수 0을 표현한다는 뜻
• 2진수 1을 표현하는 비트 패턴 (00000001) 은 지수에서는 -126을 표현함
• 2진수 254(11111110)은 +127을 표현함
• 2배 정밀도 수도 편향값으로 127대신 1023을 사용하는 비슷한 방식을 사용함

IEEE 754의 편리한 점은?

1. 0으로 나눴을 때 생길 수 있는 양의 무한대나 음의 무한대를 표현하는 비트 패턴 등 여러 가지 특별한 비트 패턴을 제공함
2. '수가 아님’ 이라는 뜻의 NaN 을 표현하는 특별한 값도 있음.
3. 부동소수점 수로 계산하던 도중에 NaN 값이 생기면 뭔가 잘못된 산술 연산을 수행했다는 뜻

2진 코드화한 10진수 시스템

• BCD, binary-coded decimal
• BCD는 4비트를 사용해 10진 숫자를 하나 표현함
  • ex) 12를 2진수로 표현하면 1100, BCD로 표현하면 0001 0010
  • 0001은 십의 자리에 있는 1을, 0010은 일의 자리에 있는 2를 표현함
• BCD가 2진수를 효율적으로 활용하지 못하기 때문에, BCD 시스템의 인기가 줄어들게됨