작성자: 이성범
0. Intro
이번 장에서는 2 종류 이상의 edge(=relation)을 가진 Graph를 다루는 방법에 대하여 학습한다. 이렇게 2 종류 이상의 edge을 가진 Graph를 Heterogeneous Graphs라고 한다.
Heterogeneous Graphs 는 다음과 같이 정의할 수 있다.

Heterogeneous Graphs는 2종류 이상의 Edge or Node를 가지기 때문에 각각의 type을 지정해주는 부분이 추가된 것을 확인할 수 있다.
- Heterogeneous Graphs를 다루기 위해 앞으로 우리가 배울 것
- Relational GCNs
- Knowledge Graphs
- Embeddings for KG Completion
1. Relational GCNs
1) GCN
우리가 지금까지 다뤘던 GCN은 다음과 같은 1개의 relation type을 가진 edge가 존재하는 그래프만을 다룰 수 있었다.
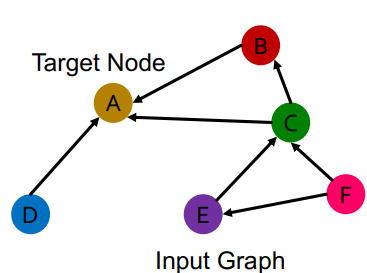
Node A를 표현하기 위해서 다음과 같이 Message와 Aggregation을 거쳐야 한다.
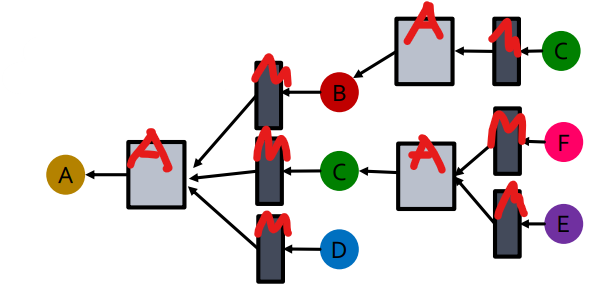
GCN을 식으로 나타내면 다음과 같다.
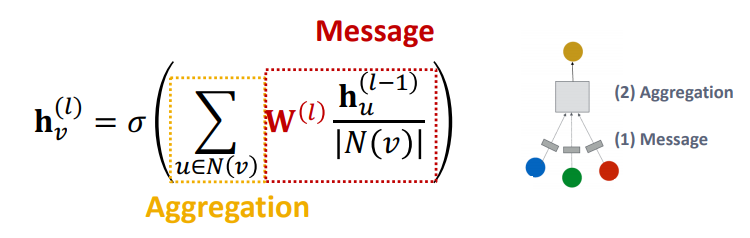
GCN은 하나의 Layer의 Message마다 W가 동일하기 때문에 1개의 relation 형태를 가진 그래프만을 표현할 수 있다. 따라서 이러한 GCN을 조금 변형시켜서 우리는 2개 이상의 relation 형태를 가진 그래프를 표현할 수 있는 Relational GCN에 대하여 학습할 것이다.
2) Relational GCN
우리가 이번에 배울 Relational GCN은 다음과 같이 2개 이상의 relation type을 가진 그래프를 다룰 수 있다.
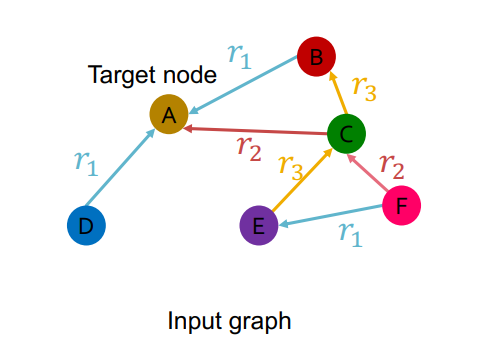
다음과 같이 각 relation의 type 마다 서로 다른 W를 학습함으로 써 2개 이상의 relation 형태를 가진 그래프를 표현할 수 있다.
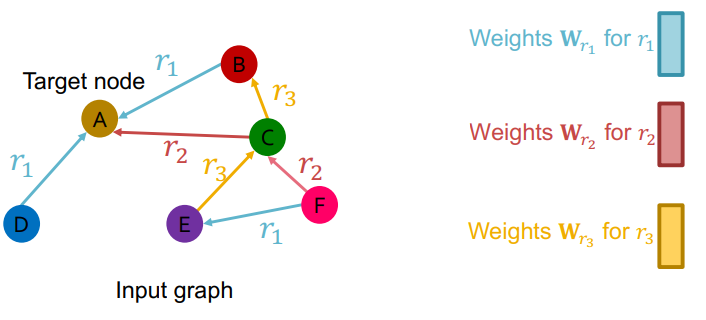
Relational GCN은 다음과 같이 relation의 type이 같은 Message를 동일한 W를 사용하고 Aggregation을 거침으로써 Node A를 표현한다.
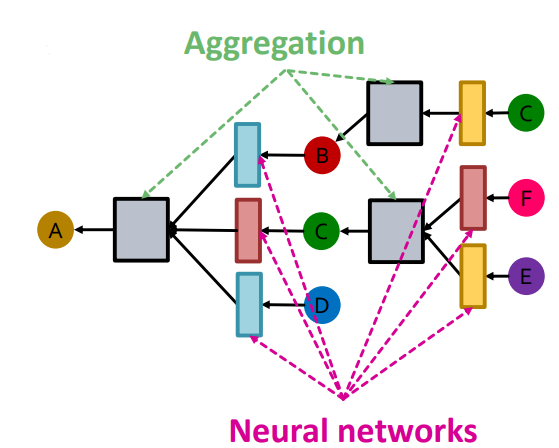
RGCN을 식으로 나타내면 다음과 같다.
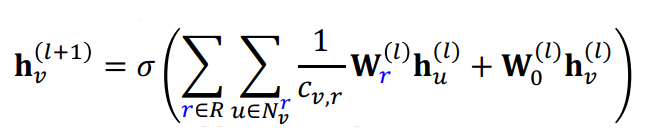
다음의 식은 그림과 같이 Self-loop의 Message를 표현하는 부분이다.
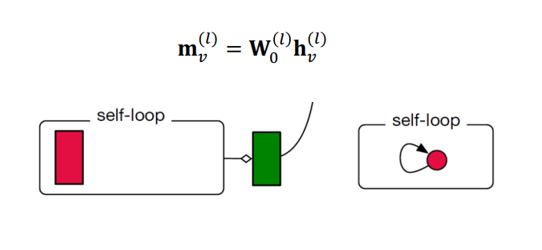
다음의 식은 GCN과 동일하게 정규화를 해주는 부분이다.
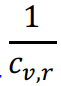
다음의 식은 그림과 같이 주변 노드의 Message를 표현하는 부분이다.
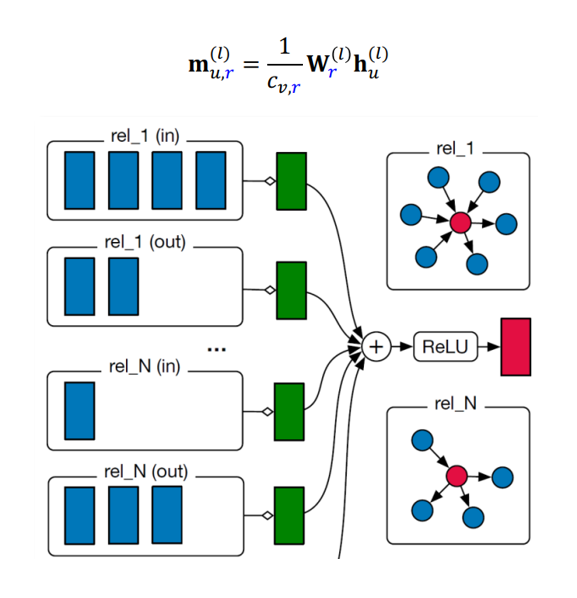
지금 까지의 Message를 다음의 식에 Aggregation과 활성화 함수 부분을 거쳐 Node를 표현하게 된다.
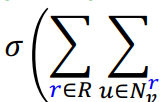
RGCN에서는 다음과 같이 각 레이어 마다 모든 r에 대한 W를 가지고 있기 때문에 r의 type 많아 진다면 Overfitting이 발생하기 매우 쉽다.(param의 수가 많아지기 때문에)
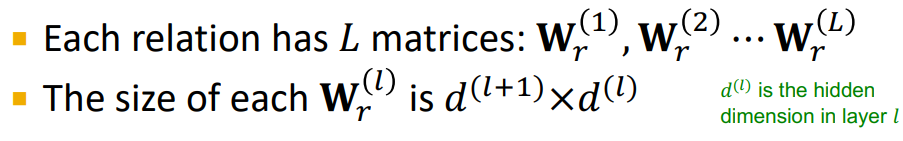
따라서 다음과 같은 2가지 방법으로 W에 regularization을 적용해준다.(param의 수를 줄이는 것)
- Use block diagonal matrices
- Basis/Dictionary learning
(1) Block Diagonal Matrices
Block Diagonal Matrices의 Key insight는 W를 sparse하게 만드는 것이다. 다음의 그림처럼 W_r을 Block처럼 대각선으로 쌓는 것이 Block Diagonal Matrices 이다.
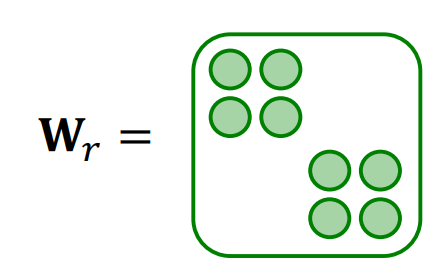
Block Diagonal Matrices을 사용하면 다음 처럼 param의 수를 줄일 수 있다.
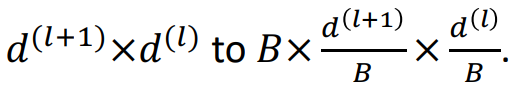
예를 들어 (relation, input dim, output dim) 형태의 (100, 32, 16) W의 param의 수는 총 51,200개 이다. 이 W에 Block Diagonal Matrices을 적용하면 (relation, block, input dim / block, output dim / block) 형태로 변환되어 (100, 4, 8, 4) 가 W가 되어 총 param의 수는 12,800(100 x 4 x 8 x 4)개로 줄어들게 된다.
(2) Basis Learning
Basis Learning의 Key insight는 W를 공유하는 것이다. 다음의 그림처럼 W_r을 linear combination of basis transformations으로 표현하는 것이 Basis Learning이다.
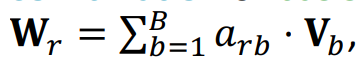
V_b는 기저행렬을 의미하고 a_rb는 V_b의 W에 모음이다. 예를 들어 (relation, input dim, output dim) 형태의 (100, 32, 16) W의 param의 수는 총 51,200개 이다. 이 W를 Basis Learning으로 나타내면, a_rb는 (relation, basis)의 형태이기 때문에 (100, 30)이 되고 V_b는 (basis, input dim, output dim)의 형태이기 때문에 (30, 32, 16)이 된다. 따라서 전체 param의 수는 18,360(100 x 30 + 30 x 32 x 16)개로 줄어들게 된다.
2. Knowledge Graphs
- Knowledge Graph : 지식을 그래프 형태로 나타낸 것
- Node == entity (Node는 type으로 label됨)
- Edge == relationship (type이 존재함)
- KG는 heterogeneous graph의 하나의 종류
Knowledge Graph의 예로는 다음과 같이 Bibliographic Networks와 Bio Knowledge Graphs 등이 있음
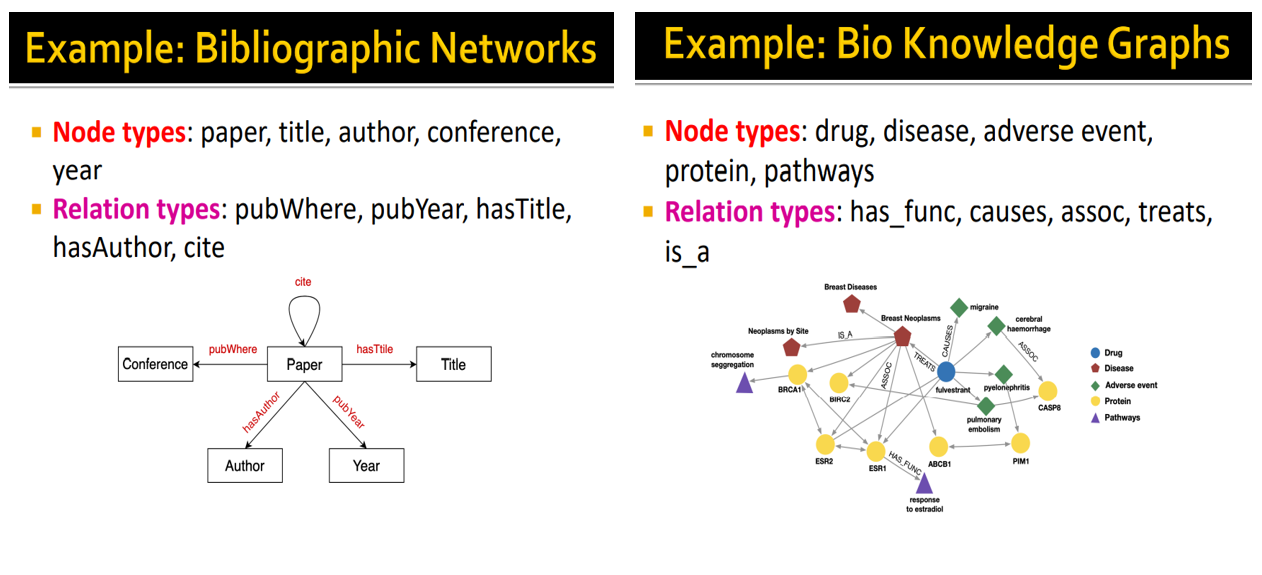
이 밖에도 Knowledge Graph를 이용하는 다양한 사례가 존재함. 이처럼 각 기업은 Knowledge Graph를 사용함으로써 Web 검색기능 개선(Google Knowledge Graph) 등 자신의 Task에 맞추어 사용함

- 공개적으로 사용가능한 Knowledge Graph Dastaset
- FreeBase, Wikidata, Dbpedia, YAGO, NELL, etc.
- 공통적으로 Massive(node와 edge가 매우 많이 존재), Incomplete(많은 edge 들이 누락되어 있음) 하다는 특징을 가짐
- 따라서 Knowledge Graph에서는 누락된 edge을 예측함으로써, Knowledge Graph 완성 시키는 것이 주요 Task임
3. Embeddings for KG Completion
Knowledge Graph를 완성시키는 것은 (head, relation)이 주어졌을 때 누락된 tail을 예측하는 것이다. 한마디로 누락된 tail을 찾음으로써 (head, relation, tail)을 만들어 edge를 만든다는 것이다. 이러한 측면에서 볼 때 link prediction task와 다르다고 할 수 있다!
다음의 그림과 같이 J.K. Rowling 과 genre가 주어졌을 때 Science Fiction을 찾는 것이, 바로 Knowledge Graph를 완성시키는 것이라고 할 수 있다. 이를 간단하게 설명하면 J.K. Rowling(해리포터 작가)과 관계가 있는 genre가 무엇 인지를 찾아보니 Science Fiction이 나오는 느낌이라고 보면 된다! 여기서 J.K. Rowling과 Science Fiction은 entity가 되고(서로 성질이 다른 Node) 두 entity간의 edge의 relation type이 genre가 될 것이다.
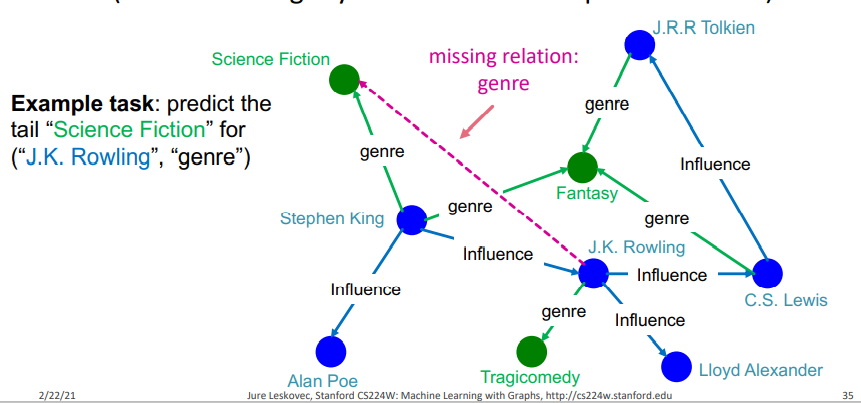
- KG Representation
- KG에서 Edge는 (h, r, t)로 표현된다.
- h == head, r == relation, t == tail
- 들어가기 전 Key Idea
- entity와 relation을 embedding space로 모델링하는 것
- (h, r, t)가 주어졌을 때, 우리의 목표는 (h, r) 임베딩과 가까운, (t) 임베딩을 찾는 것
- 따라서 (h, r)을 임베딩 하는 방법과 가까움을 정의하는 방법에 대하여 학습
우리는 앞으로 Knowledge Graph를 완성시키기 위해 KG를 embedding space에 Representation 하는 Model들을 학습할 것 이다.
그런데 Knowledge Graph는 relation pattern이 다음의 그림 처럼 다양함

그래서 Model들 마다 표현 가능한 relation pattern이 다르기 때문에 다양한 모델을 학습할 예정
- 앞으로 학습할 Model
- TransE
- TransR
- DistMult
- ComplEx
1) TransE
TransE는 다음과 같이 h, r, t가 존재할 때 각각을 R^d 차원으로 나타내는 것이다. 따라서 h + r이 t와 유사하면 좋은 것이다. (Word2Vec에서 왕자 - 남자 + 여자 = 공주 이런 느낌) 여기서 Scoring function이 h와 t의 가까움을 정의하는 함수임
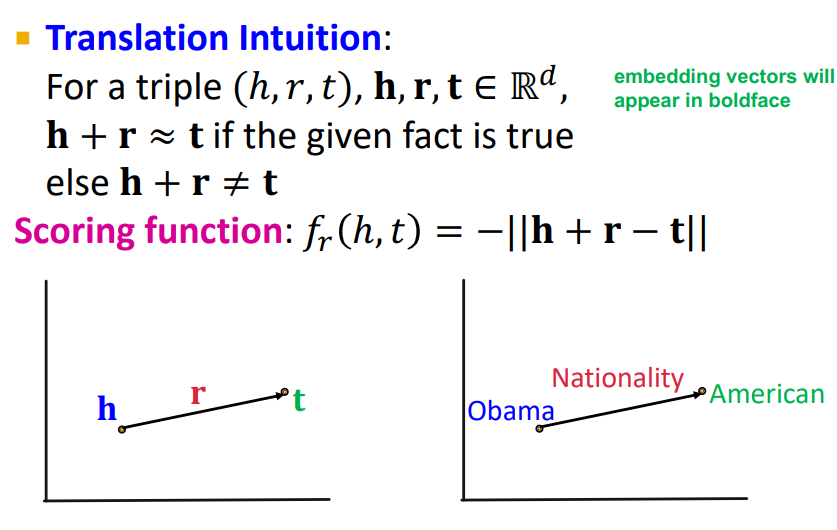
(1) Symmetric Relation
TransE는 Symmetric Relation을 표현할 수 없다. Symmetric 이란 h r t == t r h과 같은 대칭관계로 h + r = t 와 t + r = h 모두 성립해야 한다. 하지만 r은 똑같은 방향을 가지기 때문에 h + r = t 와 t + r = h 가 성립하기 위해서는 r의 값이 0이 되어야 하고 r이 0이 된다면 h == r이 되기 때문에 Symmetric Relation은 표현할 수 없다.

(2) Antisymmetric Relation
TransE는 Antisymmetric Relation을 표현할 수 있다. Antisymmetric이란 h r t != t r h과 같은 반대칭관계로 (Inverse관계와 다름) h + r = t는 성립하지만 t + r != h 가 성립하지 않아야 한다. 따라서 r은 모두 똑같은 방향을 가지기 때문에 (h + r = t) != (t + r = h) 이 되어 Antisymmetric Relations을 표현할 수 있다.

(3) Inverse Relation
TransE는 Inverse Relation을 표현할 수 있다. Inverse관계에 있는 r_1과 r_2는 r_1 = -r_2 이기 때문에 (h + r_2 = t) == (t + r_1 = h) 이 되어 Inverse Relation을 표현할 수 있다.

(4) Composition Relation
TransE는 Composition Relation을 표현할 수 있다. Composition 관계에 있는 r1, r2, r3은 r3 = r1 + r2 이기 때문에
(x + r1 = y) / (y + r2 = z) 이므로 x + r1 + r2 = z가 되어 x + r3 = z 이 되어 Composition Relation을 표현할 수 있다.
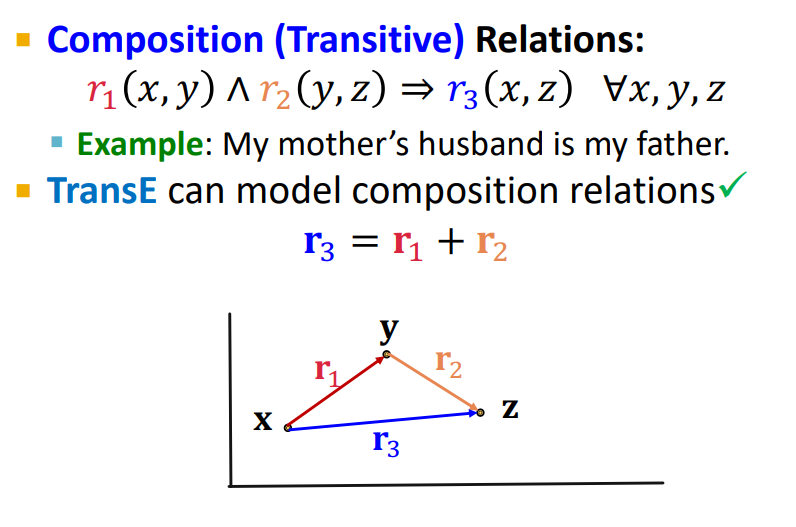
(5) 1-to-N Relation
TransE는 1-to-N Relation을 표현할 수 없다. 1-to-N Relation란, 1개의 h 에서 여러 갈래로 빠지는(똑같은 r을 가지고) t_1...t_n개가 존재하는 것이다. 그런데 여기서 r은 모두 같은 값을 가지기 때문에 h + r = t1과 h + r = t2에서 t1과 t2가 같게 되어 1-to-N Relation을 표현할 수 없다.

2) TransR
TransE는 r을 같은 임베딩 공간에 모델링한다. 하지만 TransR은 entity를 임베딩하는 공간과 relation을 임베딩하는 공간이 나뉘어지고, 이 두개를 연결짓기 위해서 projection matrix을 사용한다.(그러므로 TransE가 못하는 걸 할 수 있고, TransE가 할 수 있는 걸 못할 수 있을 것)

(1) Symmetric Relation
TransR는 Symmetric Relation을 표현할 수 있다. 우리가 아까 Symmetric Relation을 표현하기 위해서는 r이 0이라고 했는데 TransR은 entity를 임베딩하는 공간과 relation을 임베딩하는 공간이 다르기 때문에 entity를 임베딩하는 공간에서 각 entity는 다르지만 relation을 임베딩하는 공간에 투영 시킴으로써 서로 같게 할 수 있기 때문에 Symmetric Relation을 표현할 수 있다.(projection matrix의 특징)
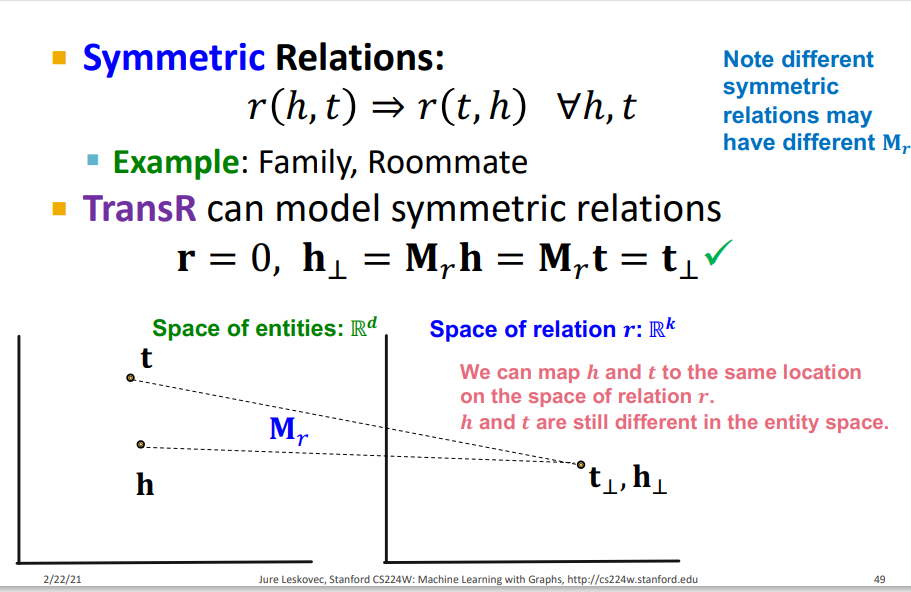
(2) Antisymmetric Relation
TransR는 Antisymmetric Relation을 표현할 수 있다. r이 0이 아니라고 한다면 r은 반대 방향으로 움직일 수 없기 때문에 (h + r = t) != (t + r = h) 이 되어 Antisymmetric Relations을 표현할 수 있다.

(3) Inverse Relation
TransR는 Inverse Relation을 표현할 수 있다. Inverse 관계란 서로 반대 방향을 가지는 r이기 때문에 TransE 처럼 (h + r_2 = t) == (t + r_1 = h) 이 되어 Inverse Relation을 표현할 수 있다.
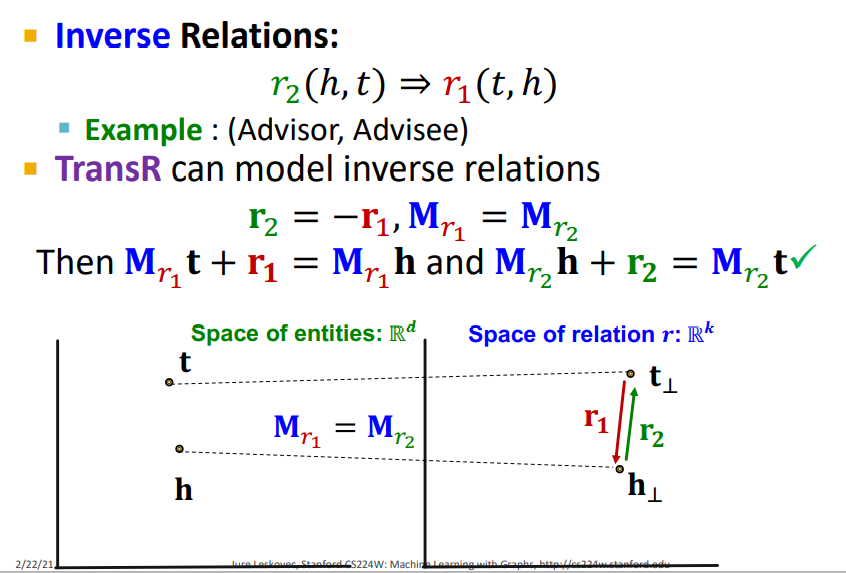
(4) Composition Relation
TransR는 Composition Relation을 표현할 수 없다. 왜냐하면 entity를 임베딩하는 공간과 relation을 임베딩하는 공간 같았던 TransE의 경우 entity1를 기준으로 r_1을 더해 entity2로 가고, 여기서 r_2를 더해entity3을 갈 수 있다. 뿐만 아니라 여기서 entity1에 r_3을 더해 entity3으로도 갈 수 있다(선형대수학의 관점). 하지만 TransR은 entity를 임베딩하는 공간과 relation을 임베딩하는 공간이 다르기 때문에 TransE 처럼 relation을 다룰 수 없기 때문에 Composition Relation을 표현할 수 없다.

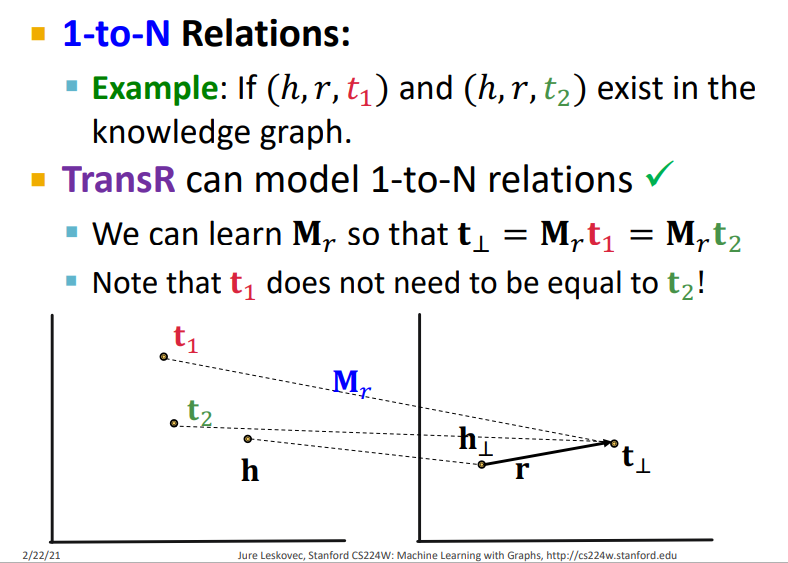
(5) 1-to-N Relation
TransR는 1-to-N Relation을 표현할 수 있다. 왜냐하면 TransR은 entity를 임베딩하는 공간과 relation을 임베딩하는 공간이 다르기 때문에 entity를 임베딩하는 공간에서 각 entity는 다르지만 relation을 임베딩하는 공간에 투영 시킴으로써 서로 같게 할 수 있기 때문에 아까 TransE에서 발생했던 h + r = t1과 h + r = t2에서 t1과 t2가 같게 되는 문제점을 해결하게 되어 1-to-N Relation을 표현할 수 있다.
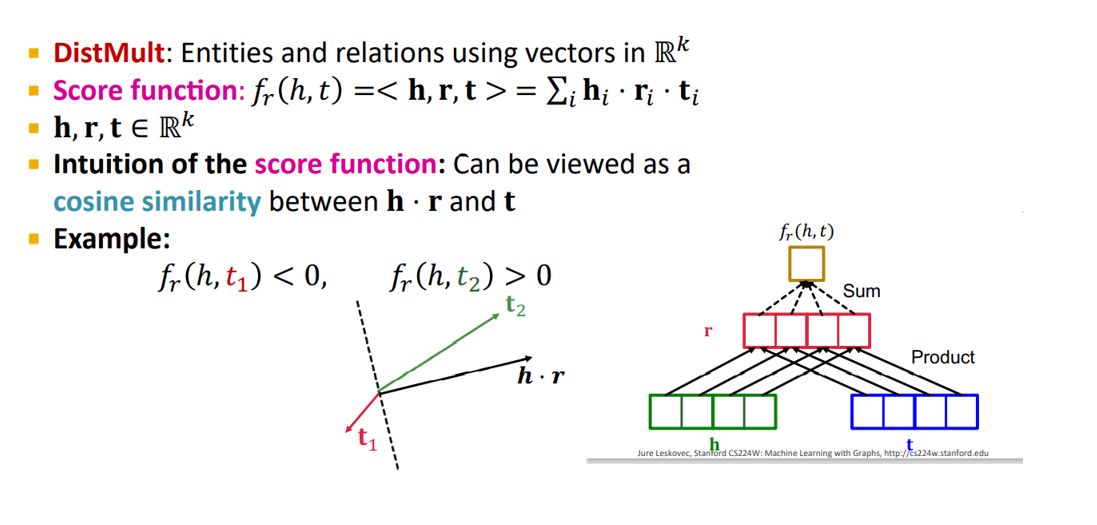
3) DistMult
DistMult는 Score function을 단순히 거리를 가지고 사용했던 TransE, TransR과 달리 h, r, t의 내적과 sum으로 나타내는 방법이다. 이러한 방법은 h * r괴 t 사이의 cosine similarity로 볼 수 있다. (즉 각도가 가까울 수록 좋음)
(1) Symmetric Relation
DistMult는 Symmetric Relation을 표현할 수 있다. 왜냐하면 h r t를 하나 t r h를 하나 동일하기 때문이다.

(2) Antisymmetric Relation
DistMult는 Antisymmetric Relation을 표현할 수 없다. 왜냐하면 h r t과 t r h이 동일하기 때문이다.

(3) Inverse Relation
DistMult는 Inverse Relation을 표현할 수 없다. 왜냐하면 왜냐하면 h r_1 t과 t r_2(=-r_1) h은 동일할 수 없기 때문이다.

(4) Composition Relation
DistMult는 Composition Relation을 표현할 수 없다. x r_1 y 와 y r_2 z 의 교집합이 x r_3 z와 같을 수는 없을 것이다. 왜냐하면 r_1, r_2, r_3 모두 다른 hyperplane으로 나타나기 때문이다.

(5) 1-to-N Relation
DistMult는 1-to-N Relation을 표현할 수 있다. 왜냐하면 h r t_1과 h r t_2는 동일할 수 없기 때문이다.

4) ComplEx
ComplEx는 Distmult와 비슷하지만, entity와 relation을 Complex vector space(스칼라를 복소수로 확장하는 것)에 임베딩한다. ComplEx는 complex conjugate를 활용하는 것이라 볼 수 있는데 complex conjugate이란 아래의 그림과 같이 x축에 의하여 대칭인 두 개의 복소수 와 있다면 의 complex conjugate를 라 한다.
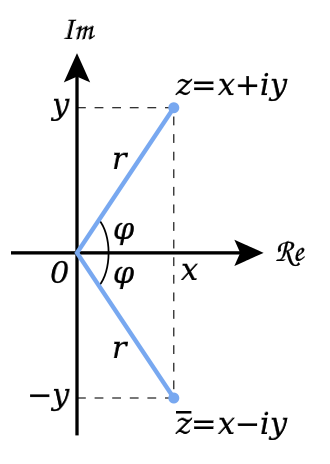
아래의 그림을 기준으로 설명하면 그냥 h와 t가 서로 complex conjugate인 관계를 찾는 것이라고 볼 수 있다. (대칭인 관계)

ComplEx의 Score function은 다음과 같다.
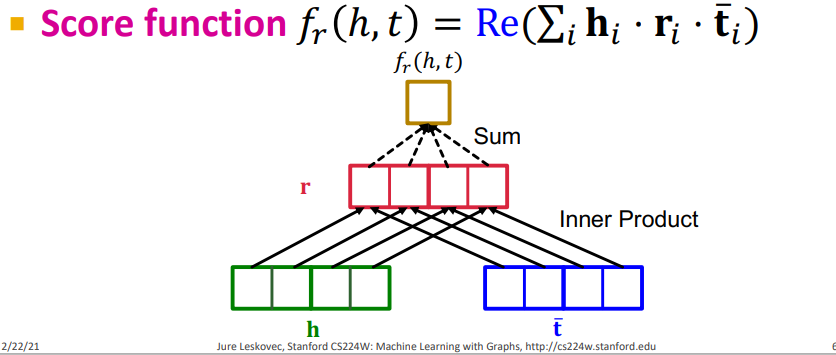
(1) Symmetric Relation
ComplEx는 Symmetric Relation을 표현할 수 있다.

(2) Antisymmetric Relation
ComplEx는 Antisymmetric Relation을 표현할 수 있다.

(3) Inverse Relation
ComplEx는 Inverse Relation을 표현할 수 있다.

(4) Composition Relation
ComplEx는 Composition Relation을 표현할 수 없다. Distmult와 같은 이유로!
(5) 1-to-N Relation
ComplEx는 1-to-N Relation을 표현할 수 있다. Distmult와 같은 이유로!
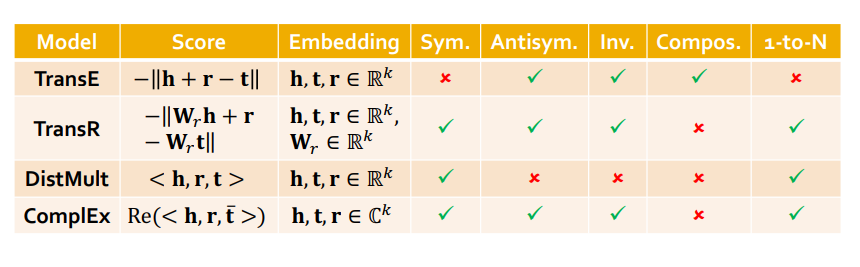
5) 정리
각 모델의 특징은 다음과 같이 표로 정리할 수 있다.