
작성자: 이성범
0. Intro
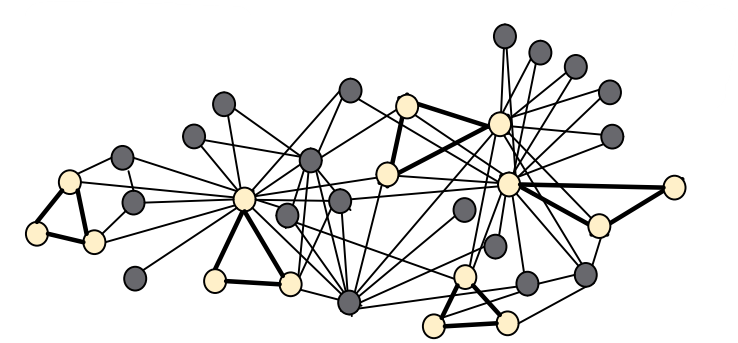
- Subgraph는 building blocks of networks 이다.
- Subgraph를 통해서 네트워크를 특징지을 수 있고 식별할 수 있다.
Subgraph를 레고로 예를 들면 작은 동일한 레고들이 모여서 하나의 큰 레고를 형성하듯이 여기서 작은 동일한 레고가 Subgraph라고 할 수 있다.
본 장에서는 다음을 다룬다.
1) Subgraphs and motifs
- Defining Subgraphs and Motifs
- Determining Motif Significance
2) Neural Subgraph Representations
3) Mining Frequent Motifs
1. Subgraphs and Motifs
Subgraphs와 Motifs는 그래프의 구조적 insights를 제공해주는 중요한 concepts이기 때문에, Subgraphs와 Motifs의 개수를 셈으로써 우리는 노드나 그래프의 features로 사용할 수 있다.(features로 사용할 수 있다는 것은 다양한 Task로 발전시킬 수 있다는 것, 예측이나...) 따라서 우리는 Subgraphs와 motifs의 개수를 세는 방법을 이번 목차에 다룰 것이다.
(나는 Motifs를 Subgraphs에 포함되거나 동일한 개념으로 이해를 했음)
1) Subgraphs
Subgraph는 2가지 방법으로 정의할 수 있음
- Node-induced subgraph
- Take subset of the nodes and all edges induced by the nodes
- 노드를 중요하게 보느냐
- Edge-induced subgraph
- Take subset of the edges and all corresponding nodes
- 엣지를 중요하게 보느냐
Subgraph를 정의하는 2가지 방법 중 Best는 도메인에 따라서 달라진다.
예를 들어 Chemistry일 경우 노드가 중요하기 때문에 Node-induced를, Knowledge graphs일 경우 엣지(관계)가 중요하기 때문에 Edge-induced를 사용함.
Graph에서는 두 개의 그래프가 서로 같은 지를 아는 것이 중요한데, 이러한 문제를 Graph isomorphism problem 라고 함
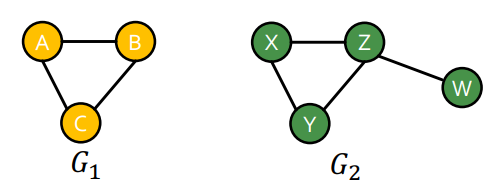
예를 들어서 위와 같은 그래프가 주어졌을때, 우리는 두 개의 그래프가 완전히 다르다고 말할 수 있을까? 우리는 대부분 안 에 이 포함되어 있다고 말할 것이다. 이러한 그래프의 isomorphism을 조금 더 확실하게 구분하기 위해서는 Node와 Edge를 가지고 서로 두 그래프를 비교해보는 것이다.

위 처럼 두 그래프는 시각적으로 모두 다른 그래프 처럼 보이지만 첫번째 그래프의 경우에는 각 노드와 연결된 엣지를 기준으로 비교해본다면 서로 같은 그래프이다. 두번째 그래프의 경우 각 노드에 연결된 엣지가 다르니 다른 그래프이다. 이처럼 Node와 Edge를 가지고 서로 두 그래프를 비교하면 두 그래프의 isomorphism 판단할 수 있다.
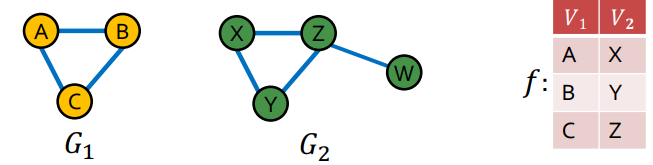
과 의 node를 각각 match 시키면 우리는 과 사이에
동일한 subgraph를 가진다는 것을 알 수 있다. 따라서 우리는 과 는 다른 그래프지만 은 의 subgraph 라고 할 수 있다.
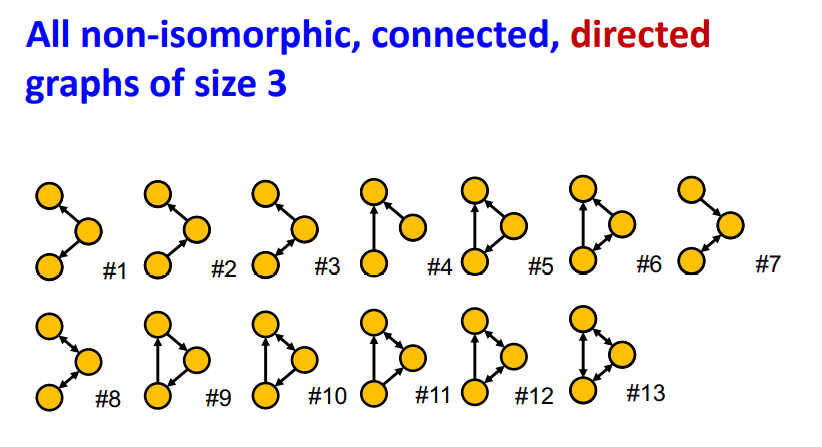
이처럼 subgraph는 시각적으로는 비슷해 보이지만 Node와 Edge(Edge의 방향)에 따라서 그래프 크기가 같더라도 다양한 non-isomorphic 관계인 subgraph가 존재한다.
2) Motifs
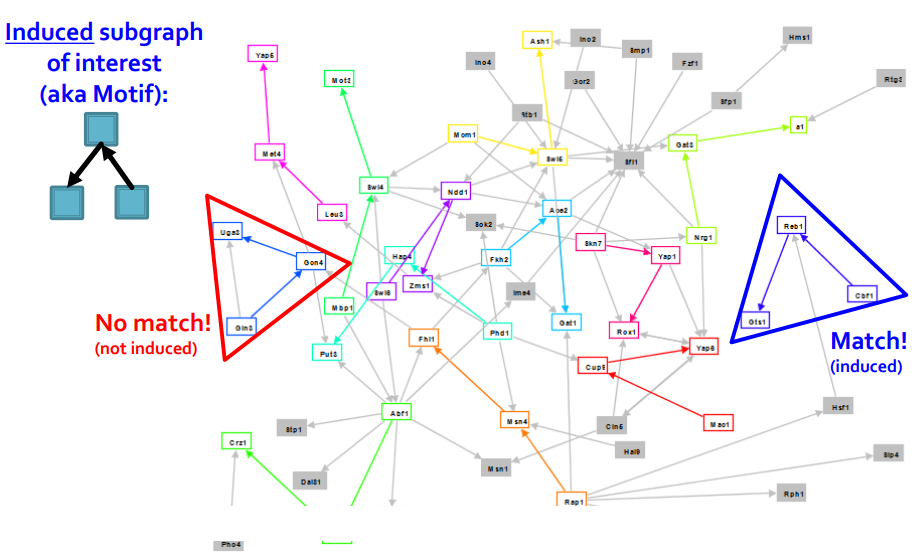
Network Motifs는 recurring, significant patterns of interconnections으로 정의된다. Network Motifs를 정의하기 위해서는 3가지 개념을 알아야 한다.
- Pattern : Small (node-induced) subgraph / 그림에 Induced subgraph
of interest 와 같은 유도될 수 있는 subgraph의 패턴 - Recurring : Found many times, i.e., with high frequency / 발생 빈도
- Significant : More frequent than expected, i.e., in randomly generated graphs? / real graph와 random으로 생성된 graph를 비교하는 것

그러면 왜 Motifs가 필요할까? Motifs는 그래프가 어떻게 작동하는지에 대해 이해하는데 도움을 주며, 그래프 데이터셋에서 예측을 하는데 도움을 준다.
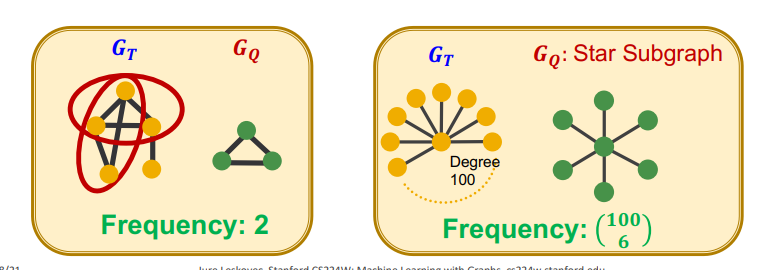
만약에 데이터셋에 여러 개의 그래프가 포함되어 있고 데이터셋의 subgraphs 빈도를 계산하고 싶다면, 데이터셋을 개별 그래프에 해당하는 분리된 구성 요소를 가진 거대 그래프 G로 취급하여 subgraphs를 count하면 된다. 그림과 같이 를 target graph dataset으로 두고 를 small graph로 두어 안에 존재하는 를 세면 subgraphs 빈도가 된다.
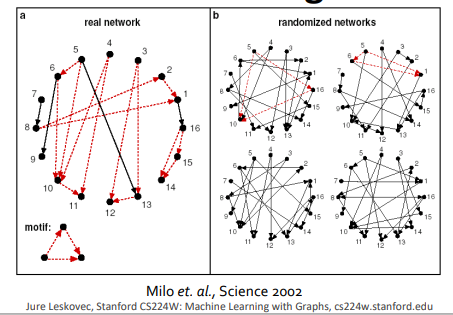
Motif Significant는 랜덤으로 생성된 network와 비교하고자 하는 network(real)에서 주어진 motif의 발생 빈도를 비교하여 계산한다.
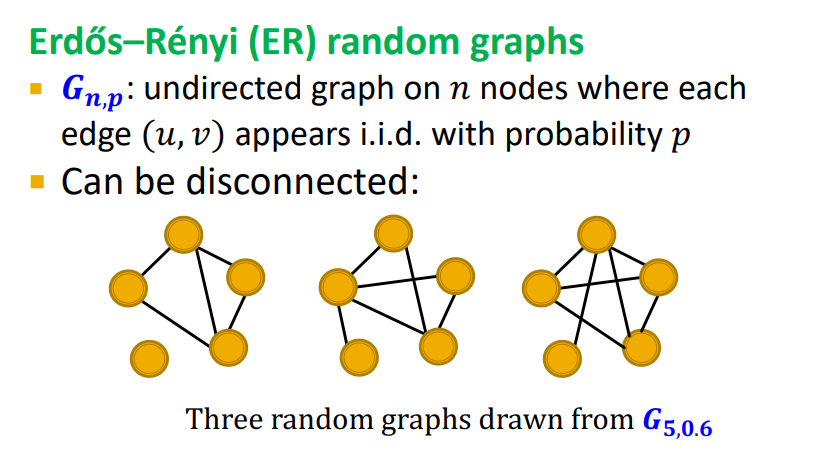
Random Graphs를 정의하는 방법 중 한 가지는 Erdős–Rényi random graphs 이다. n개의 노드를 정하고 각 노드를 연결하는 엣지를 생성할 확률 p를 정하여 random graph를 생성하는 방법이다.
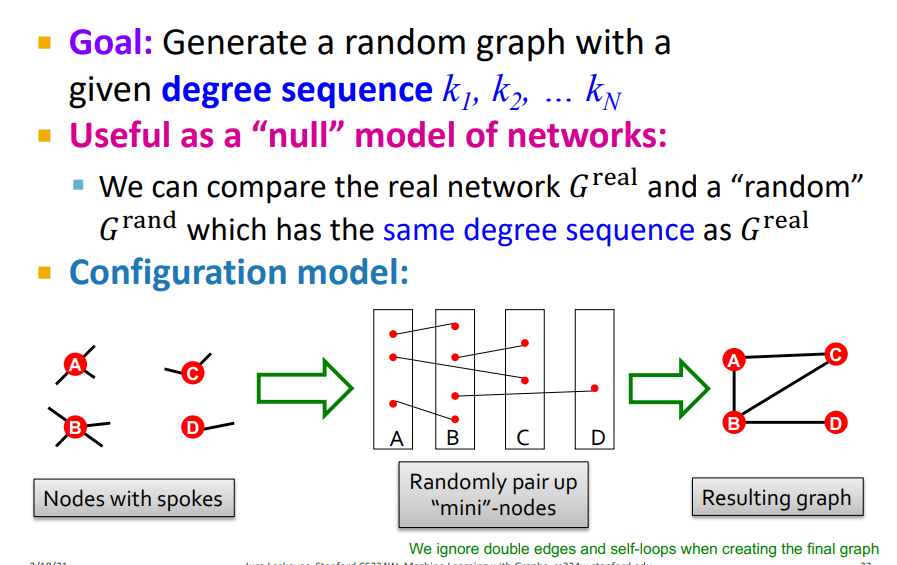
또 다른 방법은 Configuration model이다. Configuration model은 주어진 degree sequence를 사용하여 random graph를 생성하는 방법이다. 하나의 노드가 주어지면 각 노드는 degree가 존재한다. 이 각 노드에 존재하는 edge의 개수, 즉 degree를 하나의 작은 node로 생각하여 각 노드를 무작위로 연겷한다. 이 연결선이 1개 이상 존재하면 마지막과 같이 그래프의 Node를 연결하여 random graph를 생성한다. (여기서 Node degree를 spokes 라고 부르는 것 같음)

또 다른 방법은 Switching이다. Switching은 그림과 같이 A->B / C->D 로 연결되는 edge를 무작위로 선택한 후, 두 edge의 endpoint를 서로 교환하여 A->D / C->B 로 연결되는 edge로 바꾸어 random graph를 생성하는 방법이다. 따라서 Switching은 random으로 생성된 그래프와 비교될 그래프의 node degree가 서로 같다는 특징을 가진다.(Configuration model은 node degree가 달라질 수 있음)
Motif Significant를 계산하는 과정은 총 3 Step으로 이루어 진다. 우리는 지금 까지 Step 1, 2를 다뤘고 이제 각각의 모티브가 통계적으로 얼마나 유의한지에 대하여 측정하는 방법인 Step 3을 배울 것임
- Step 1 : Count motifs in the given graph ()
- Step 2 : Generate random graphs with similar statistics (e.g. number of nodes, edges, degree sequence), and count motifs in the random graphs
- Step 3 : Use statistical measures to evaluate how significant is each motif

Motif Significant는 Z-score와 비슷한 개념이다. 랜덤으로 생성된 network의 motif의 발생 빈도의 평균과 표준편차를 사용하고 여기서 랜덤으로 생성된 network를 모집단으로 사용하여 Z-score를 구한다. 우리는 Network significance profile를 정규화된 Z-score의 벡터로 구할 수 있다. 일반적으로 큰 그래프일 수록 Z-score의 값이 커진다.

우리는 Z-score를 통해서 각 Subgraph에 Significance를 분류할 수 있다. 따라서 우리는 network significance profile을 만들 수 있다.
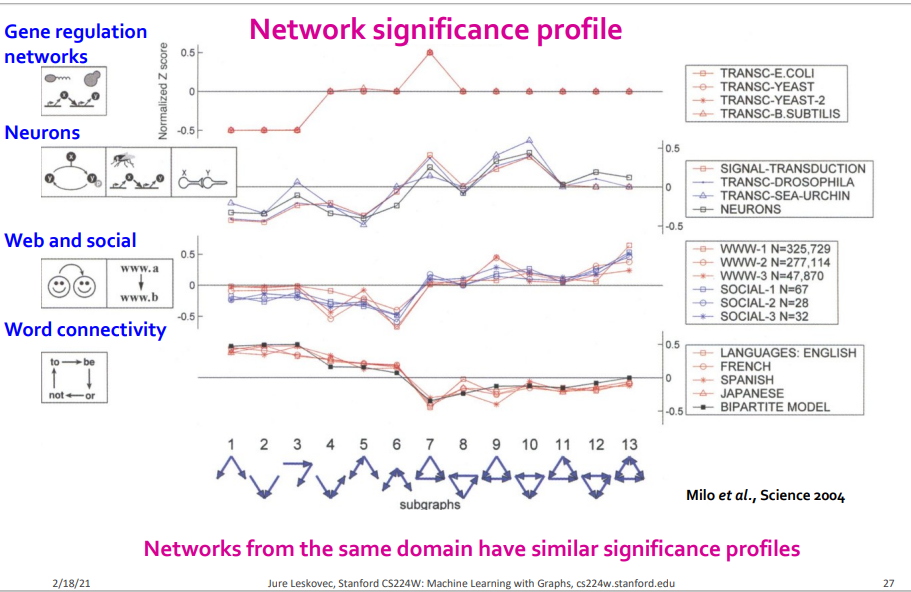
서로 다른 도메인의 network는 서로 다른 network significance profile를 가진다는 것을 알 수 있고 서로 같은 도메인의 network는 서로 같은 network significance profile을 가진다는 것을 확인할 수 있다. 따라서 우리는 network significance profile을 통해서 해당 도메인의 고유한 특성에 대한 insight를 얻을 수 있다.
- 요약
- Subgraphs and motifs are the building blocks of graphs (motifs는 graphs의 일부분)
- Understanding which motifs are frequent or significant in a dataset gives insight into the unique characteristics of that domain (motifs의 significant를 통해서 우리는 해당 도메인의 고유한 특성에 대한 insight를 얻을 수 있음)
- Use random graphs as null model to evaluate the significance of motif via Z-score (random graphs는 motif의 significance를 평가하기 위한 null model로써 사용됨)
2. Neural Subgraph Representations
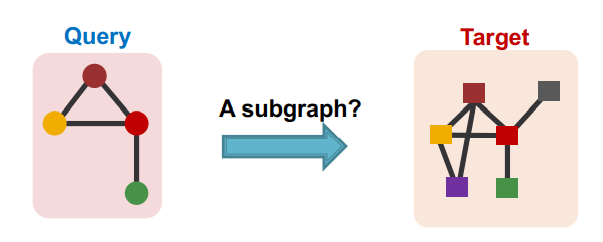
우리는 다음과 같이 Query와 Target 그래프가 주어졌을때 Query가 Target의 subgraph 인지 판단하기 위해서 embedding space의 geometric shape을 활용한다. 여기서 우리는 embedding space의 geometric shape을 구하기 위해서 GNN을 활용한다.
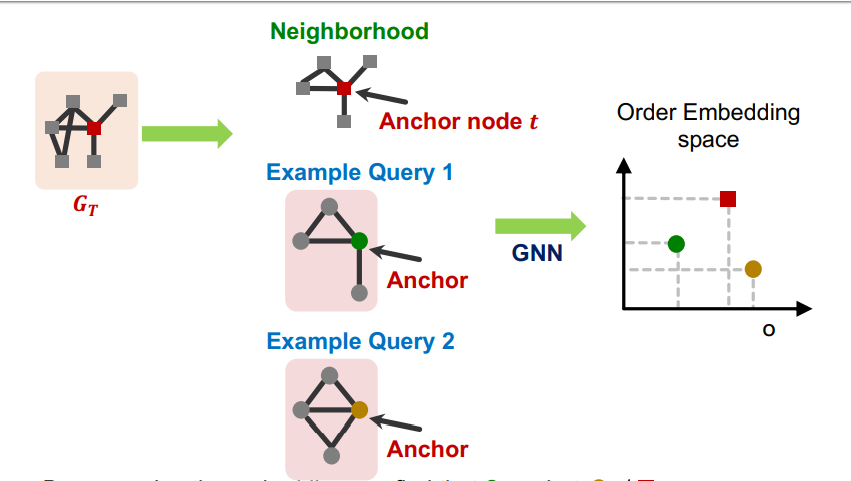
다음과 같이 embedding space 안에 Target과 Query1, Query2를 Representation했을 때 Query1은 Query1 <= Target의 관계를 가지기 때문에 Target의 Subgraph라고 할 수 있다. 그러나 Query2는 Query2 <= Target의 관계를 가지지 못하기 때문에 Target과 다른 그래프라고 할 수 있다.
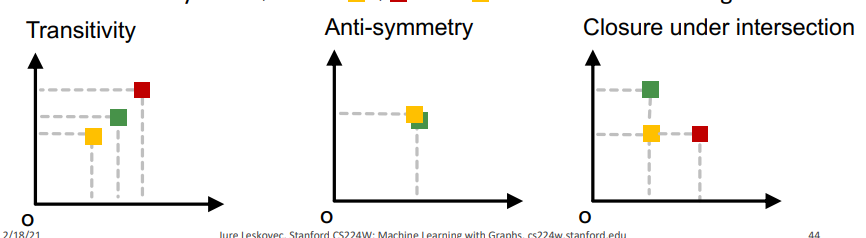
Subgraph isomorphism relationship 은 3종류로 다음과 같이 embedding space에 Representation 된다. Transitivity는 노란색 <= 초록색 / 초록색 <= 빨간색 / 노란색 <= 빨간색 의 관계를 가지는 형태로 노란색은 초록색의 Subgraph이고 초록색은 빨간색의 Subgraph이고 노란색은 빨간색의 Subgraph인 관계이다. Anti-symmetry는 노란색 == 초록색 의 관계를 가지는 형태로 노란색과 초록색이 서로 동일한 그래프인 관계이다. Closure under intersection은 노란색이 빨간색과 초록색의 부분적인 Subgraph인 관계이다.
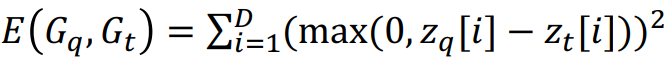
우리는 GNN을 다음과 같은 Max-Margin Loss 함수로 학습하여 embedding space 구한다. 이면 는 의 Subgraph가 이고 이면 는 의 Subgraph가 아니다.
3. Mining Frequent Motifs

가장 빈도수가 높은 size-k의 Motifs를 찾기 위해서는 다음 2가지를 해결해야 한다. 그런데 이렇게 Enumerating하고 Counting하는 것은 가능한 모든 패턴들을 조합시켜서 Combinatorial explosion을 가져오기 때문에 매우 hard computational problem 이다. 따라서 우리는 이러한 문제를 Representation learning을 통해서 해결한다.(GNN을 이용하여 그래프의 임베딩을 서로 비교하면서 두 그래프의 관계를 찾아서 해결한다는 것으로 이해함)
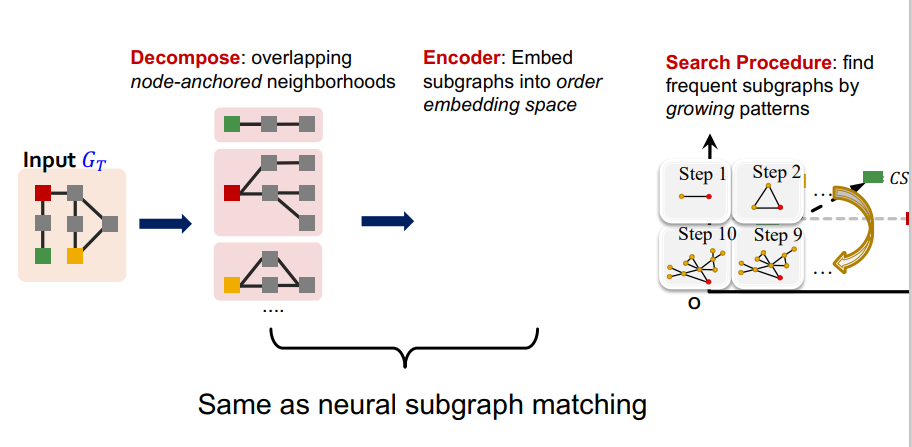
가장 빈도수가 높은 size-k의 Motifs를 찾는 하나의 neural model이 바로 SPMiner이다. 그래프를 임베딩 공간에 나타난 뒤에 주어진 Subgraph 를 모두 비교하며 Subgraph 빈도 수를 구하는 것이다. (여기서 Subgraph의 집합이 나는 size-k의 Motifs의 후보라고 이해를 했음)
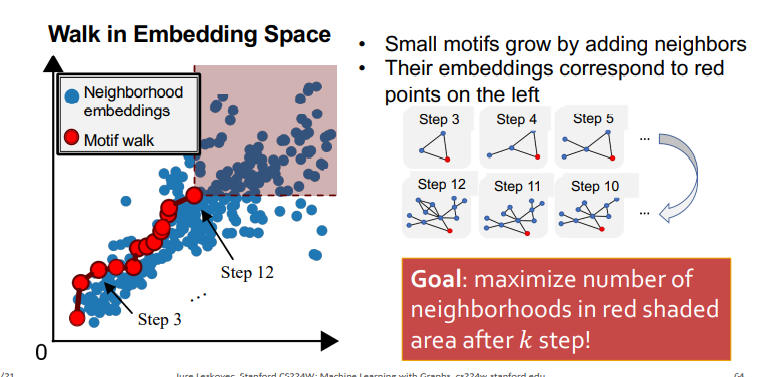
SPMiner 목표는 k step 마다 가장 많은 eighborhood embeddings를 포함하는 Motif를 찾는 것이고, 학습은 무작위로 한개의 노드를 초기의 값으로 선택한 후에 각 step 마다의 subgraph를 저장하는 과정으로 이루어지고, 지정한 k에 도달하면 학습이 멈춘다. (나는 저장된 subgraph들 중에서 자신이 원하는 size-k의 Motifs를 결정하는 것으로 이해를 함, 왜냐하면 각 스텝마다 제일 많은 Neighborhood embeddings를 포함하는 Motif들 이기 때문에)