그래프 알고리즘

SeoYng·2020년 9월 4일

다익스트라 알고리즘 최단경로 최소신장 트리 크루스칼 프림

최단경로 [다익스트라], 최소신장 트리[크루스칼, 프림] + union/find 정리

1) 최단경로 알고리즘

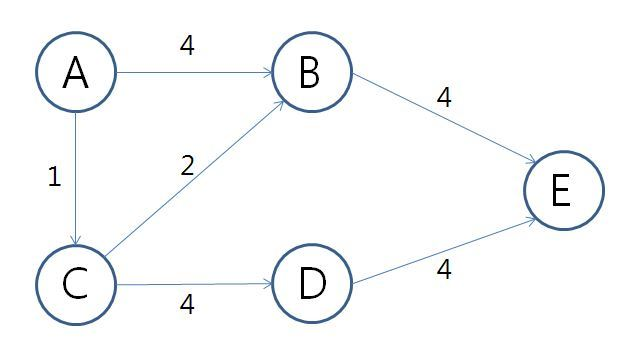
start 노드에서 end노드까지 가는데 걸리는 가장 짧은 경로

예시

A > C > B > E
1+2+4 = 7

# 다익스트라 알고리즘

첫 정점을 기준으로 연결되어 있는 정점들을 추가하며 최단거리를 갱신하는 방법
- BFS 와 유사, 큐/힙 사용

거리정보 배열 초기화
[0, inf, inf, inf ....]
큐/힙을 이용하여 BFS 형태로 인접 노드를 방문하며 거리정보 배열 업데이트
이때 기존값과 현재노드 + 간선 거리값 중 더 작은 값으로 갱신
[0, 4, 1, inf...]
...
[0, 3, 1, 5, 7]

시간복잡도 : O(ElogE)

2) 최소신장 트리(Minimun Spanning Tree)

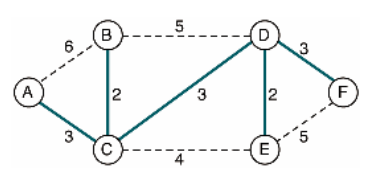
모든 노드가 연결되어 있으면서 사이클이 존재하지 않는 신장 트리 중 간선의 가중치 합이 가장 짧은 트리

예시

3+2+3+2+3 = 13

# 크루스칼 알고리즘

모든 간선을 가중치 기준으로 정렬 한후 비용이 작은 간선부터 연결시키고자 한다.
두 정점의 최상위 정점을 확인한후 다르면 연결한다
(서로 다른집합일 때, 즉 사이클이 생기지 않을 때)
모든 간선이 연결될 때까지 반복한다.

# 프림 알고리즘

시작 정점을 선택한 후 인접 간선을 힙에 넣고 가장 작은 간선을 연결시키고자 한다.
두 정점의 최상위 정점을 확인한 후 다르면 연결한다
(서로 다른집합일 때, 즉 사이클이 생기지 않을 때)
새롭게 연결된 노드에서 인접간선을 추가로 힙에 넣고 과정을 반복한다.
모든 간선이 연결될 때까지 반복한다.

개인적으로는 프림알고리즘이 더 이해하기도 구현하기도 쉬웠다.

**사이클 생성여부 - # union & find

코드

# 파이썬
parent = { n:n for i in range(1, n+1) }

def get_parent(parent, node):
    return node if parent[node] == node else get_parent(parent, parent[node])
    
def find(parent, a, b):
    return get_parent(a, node) == get_parent(b, node)
    
def union(parent, a, b):
    a, b = get_parent(a, node), get_parent(b, node)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

def union_find(parent, a, b):
    a, b = get_parent(a, node), get_parent(b, node)
    if a != b:
       if a < b:
            parent[b] = a
       else:
            parent[a] = b