알고리즘 기본

코테 빈출

https://wikidocs.net/218198
구현 ★★★★
그래프 ★★★★
DFS/BFS ★★★★★
탐욕법/Greedy ★★★★
해시 응용★★★★★
문자열 ★★★★★
이분탐색 ★★★
동적계획법 (DP) ★★★
비트 마스킹★★
슬라이딩 윈도우 & 투포인터 ★★
누적합 ★★
최단경로 ★★
정렬 ★★
백트래킹 ★★
브루트포스 ★★
분할정복 ★★

슈도코드

• 무엇을 어떻게 동작하도록 작성할 지에 대하여 사람이 이해할 수 있는 언어로 작성하는 것

시간복잡도

빅-오메가(Ω(n)) : 최선
빅-세타(θ(n)) : 보통
빅-오(O(n)) : 최악

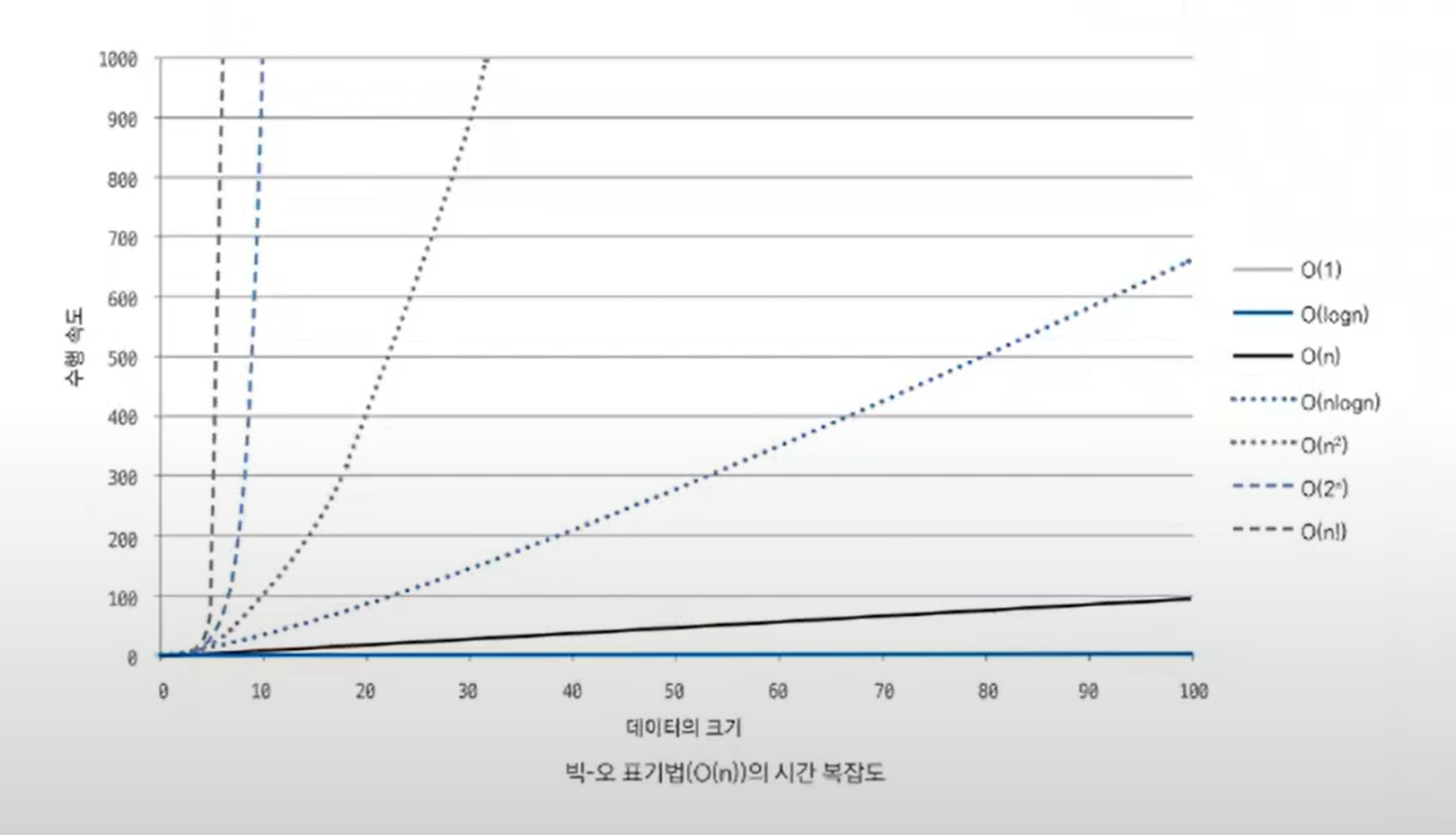
시간복잡도 도출 기준

• 상수는 제외
• 가장 많이 중첩된 반복문의 수행 횟수가 기준

시간복잡도 풀기

• 알맞은 알고리즘 선택
• 비효율적인 로직 효율적으로바꾸기

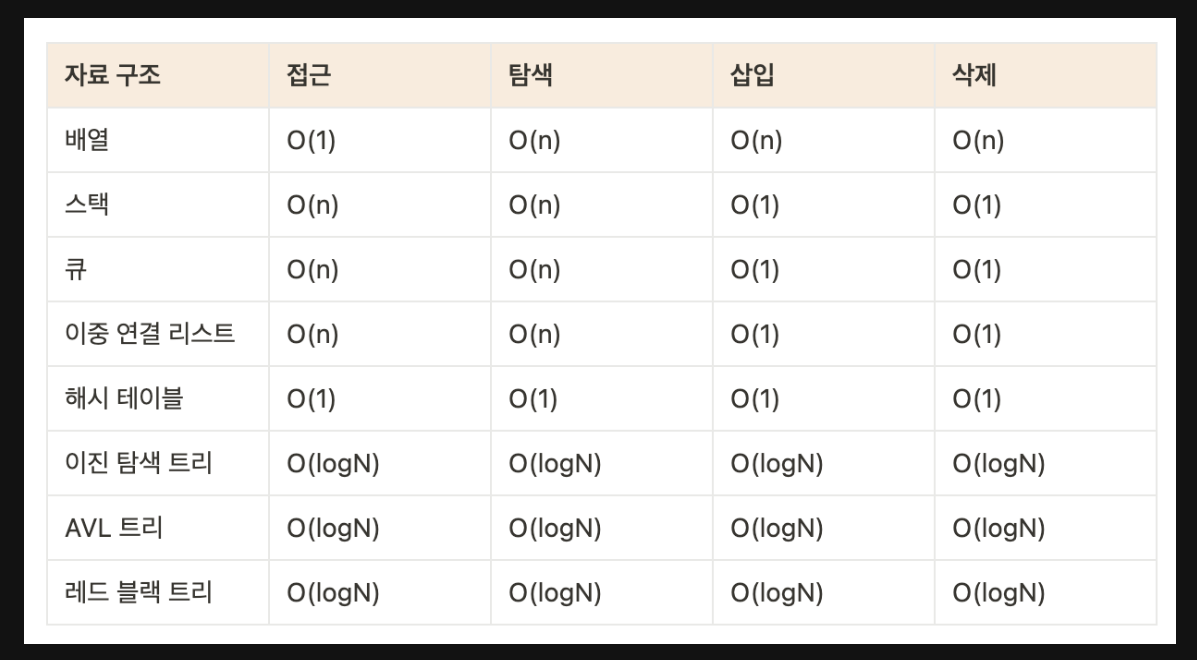
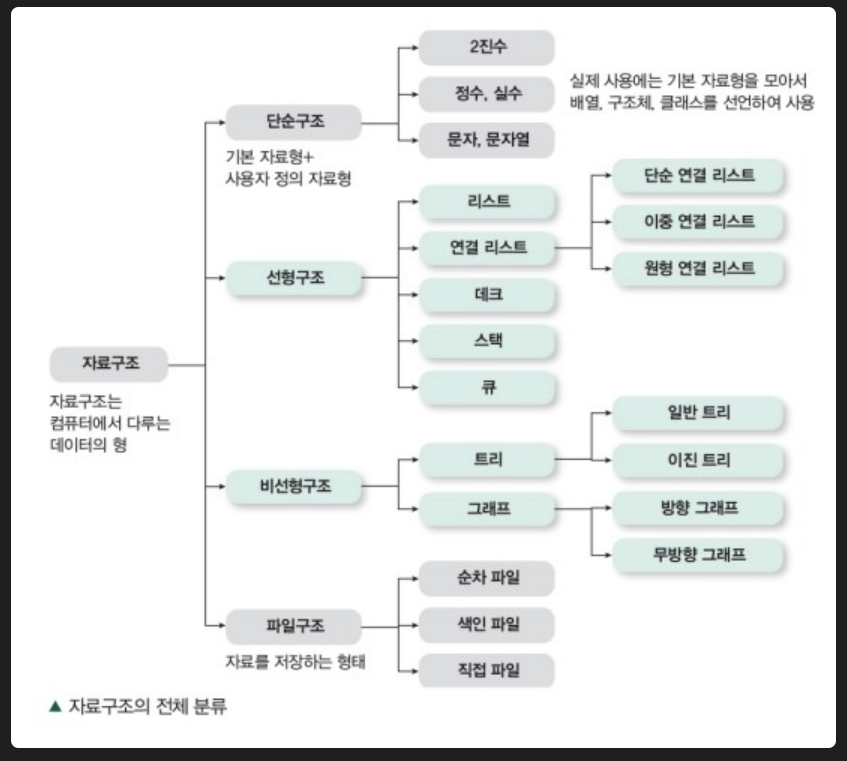
자료구조

배열과 리스트

배열과 리스트의 차이점

• 메모리 할당: 배열은 연속적인 메모리 공간에 할당되고, 리스트는 비연속적인 메모리 공간에 할당된다.

• 크기: 배열은 크기가 고정되어 있으며, 리스트는 가변적이다.

• 접근 방법: 배열은 인덱스를 통한 빠른 접근이 가능하지만, 리스트는 순차적으로 접근해야 한다.

• 삽입과 삭제: 배열은 삽입과 삭제가 번거롭고 시간이 오래 걸리지만, 리스트는 삽입과 삭제가 빠르다.

구간 합

수열에서 특정 구간의 합을 구할 때 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘

• 부분 합(Partial sum) : 처음부터 k번 인덱스까지의 합 ( = A[0] + A[1] + ... A[k] )

• 구간 합(Prefix sum) : i번부터 j번 인덱스까지의 합 ( = A[i] + A[i+1] ... + A[j-1] + A[j] )

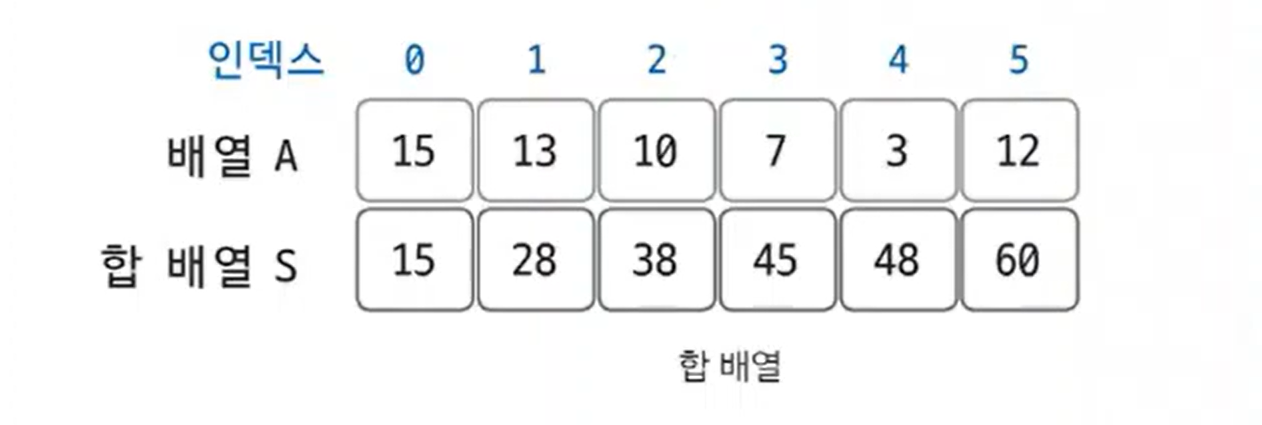
합배열 만드는 공식
S[i] = S[i-1] + A[i]

구간합 구하는 공식
S[j] - S[i-1]

투 포인터

• 2개의 포인터로 알고리즘 시간복잡도를 최적화

• 슬라이딩 윈도우
  2개의 포인터로 범위를 지정한 후 유지한체 이동하면서 문제를 해결

스택과 큐 ★★★

스택

• top : 삽임삭제가 일어나는 위치
• push, pop : 삽입, 삭제
• peek : top위치 데이터 확인
• 활용 : 우선탐색(DFS), 백트래킹, 재귀함수원리와 비슷

큐

• rear, front : 끝,앞데이터
• add : rear에 데이터 삽입
• poll : front 데이터 삭제하고(꺼내고) 확인
• peek : front 데이터 확인
• 활용 : 너비우선탐색(BFS)

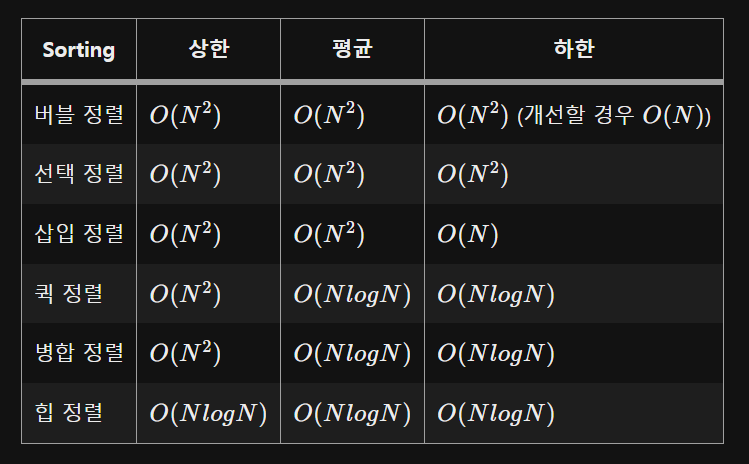
정렬알고리즘

버블 정렬 : loop돌면서 인접요소끼리 swap(n²)
선택 정렬 : 최대 나 최소데이터 찾아가며 선택
(구현방법 복잡하고 시간복잡도(n²) 코테에 잘 사용 x)
삽입 정렬 : 이미 정렬된 범위에 정렬되지 않은 데이터를 삽입(시간복잡도(n²) 코테에 잘 사용 x)

퀵정렬 : 기준값을 선정해서 작은데이터와 큰데이터로 분류 (nlogn)

병합정렬 : 분할정복방식을 사용해 데이터를 분할하고 분할한 집합을 정렬해서 합치는 알고리즘 (nlogn)

탐색 ★★★

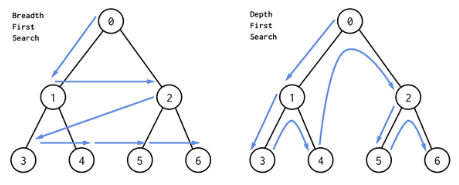
깊이우선탐색(DFS) : 그래프 완전탐색기법 중 하나 시작노드에서 출발하여 분기를 정하여 최대 깊이까지 탐색한 후 다른쪽분기로 이동

• 재귀함수로 구현 -> 스택오버플로 유의
• 스택(FILO) 자료구조 이용
• 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상정렬 등등에 활용

너비 우선 탐색(BFS) : 그래프 완전탐색기법 중 하나 시작노드에서 가까운 노드를 먼저 방문하면서 탐색

• 큐(FLFO) 자료구조

이진탐색 : 정렬되있는 상태에서 원하는 값을 찾아내는 알고리즘 중앙값과 찾고자하는값을 비교해 절반씩줄이면서 탐색

그리디 알고리즘 ★★★

현재 상태에서 보는 선택지 중 최선의 선택지가 전체 선택지 중 최선의 선택지라고 가정하는 알고리즘

• 해 선택 : 현재상태에서 가장최선이라고 생각되는 해 선택
• 적정성 검사 : 문제의 제약조건에 벗어나지않는지 검사
• 해 검사 : 전체문제를 해결할 수 있는지 검사

소수 구하기

• 대표적인 판별법으로는 에라토스테네스의 체 원리가 있습니다.
• 에라토스테네스의 체 : 작은 수부터 배수를 지워나가는 방법

오일러피 함수

서로소인 자연수의 개수

• 배열을 탐색하며 P[i] = P[i] - P[i]/K 수행(i는 K의 배수)

유클리드 호제법

두 수의 최대공약수(GCD)를 구하는 알고리즘 (MOD 연산)

그래프 ★★★

노드와에지로 구성된 집합

• 유니온 파인드 : 사이클이 생성되는지 판별하는 알고리즘

• 위상 정렬 : 싸이클x, 방향이 있는 그래프일때 그래프의 노드들을 선형으로 정렬(정렬 결과가 꼭 한개는 아님)
  i) 수강신청
  i) 게임 빌드오더

• 최단거리 알고리즘

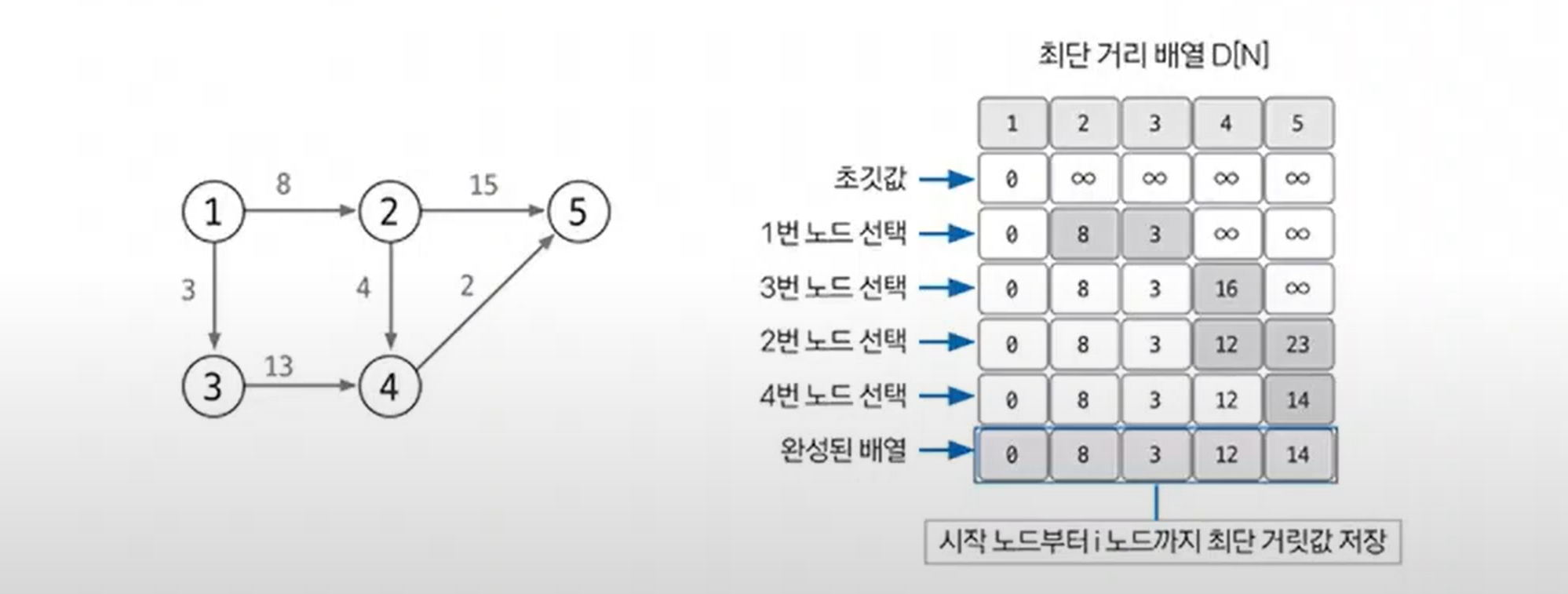
  1. 다익스트라 : 시작점이 있고 다른노드로 가는 최단거리를 구하는 알고리즘(단, 음수간선은 있으면 안된다)
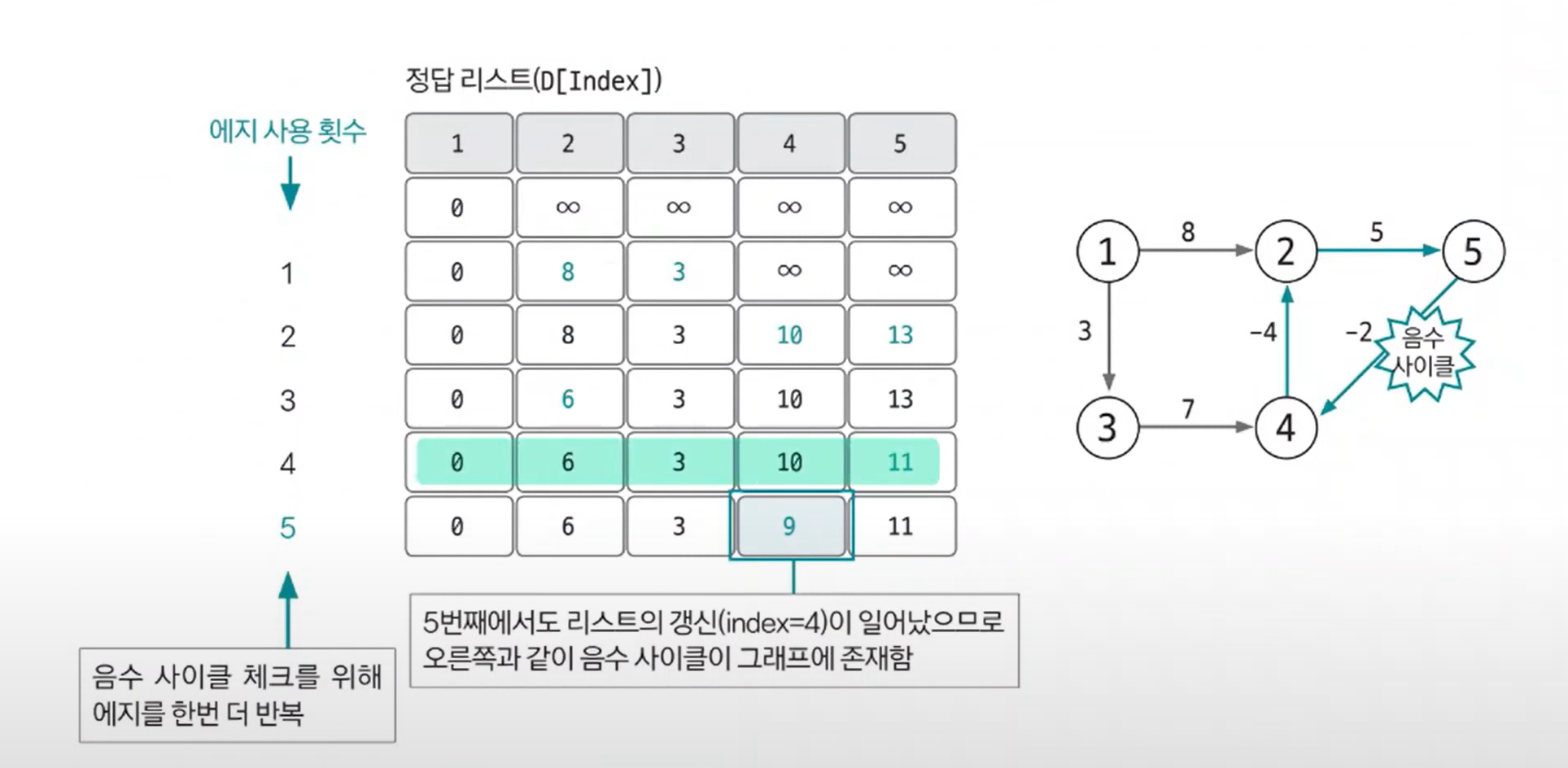
  2. 벨만-포드 : 시작점이 있고 다른노드로 가는 최단거리를 구하는 알고리즘(음수간선도 ok)
     i) 음수 싸이클있는지 체크하는문제
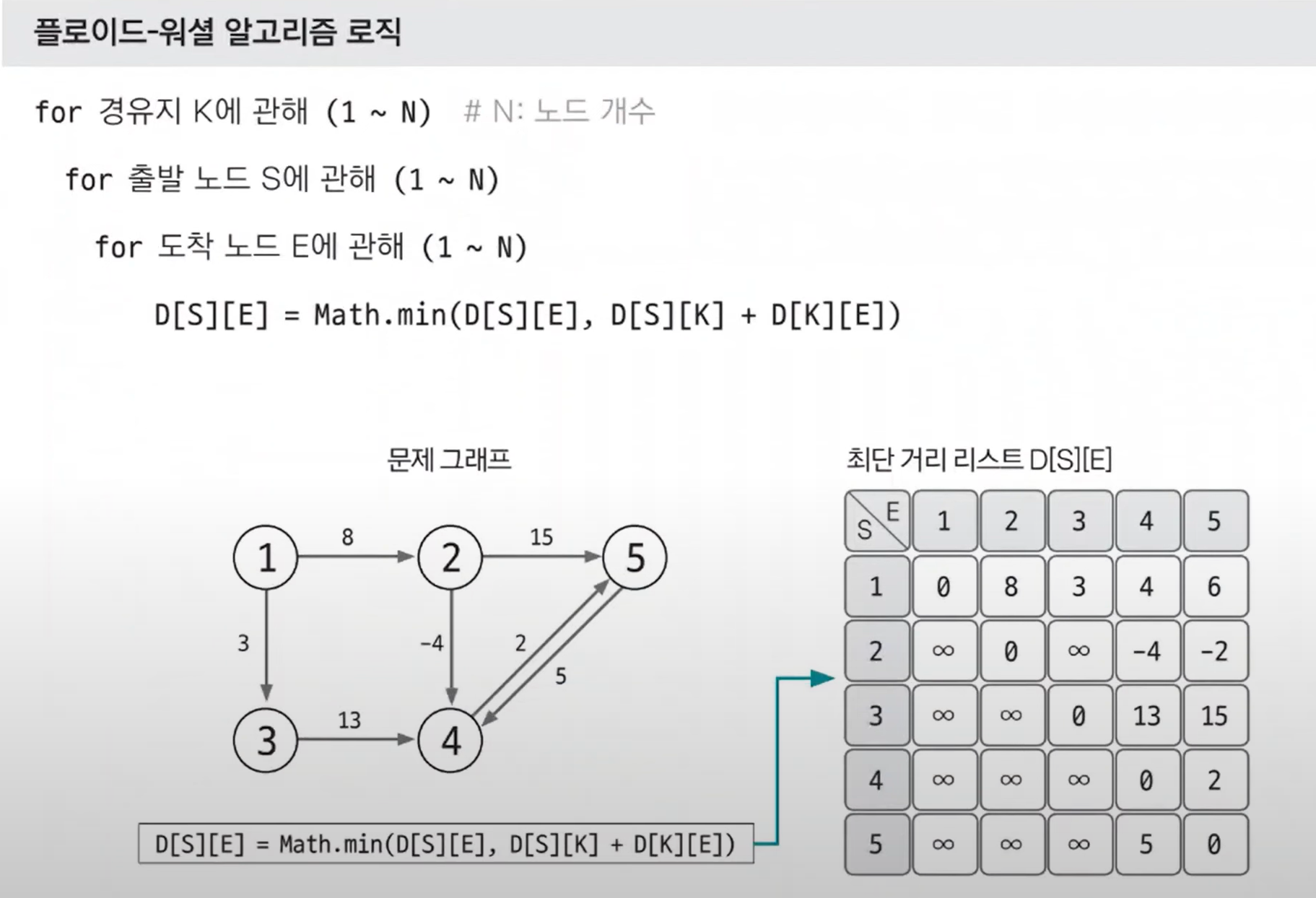
     ii) 시간여행, 웜홀 등등
  3. 플로이드-워셜 : 시작점없이 최단거리를 구하는 알고리즘 (시간복잡도 불리)
     i) 모든 도시안에 최단거리

• 최소 신장 트리 (MST) : 그래프에서 최소의 가중치 합으로 모든 노드를 연결할수있게 해주는 알고리즘
  i) 유니온 파인드 필요 (싸이클 나올 수 없게끔 방지용)

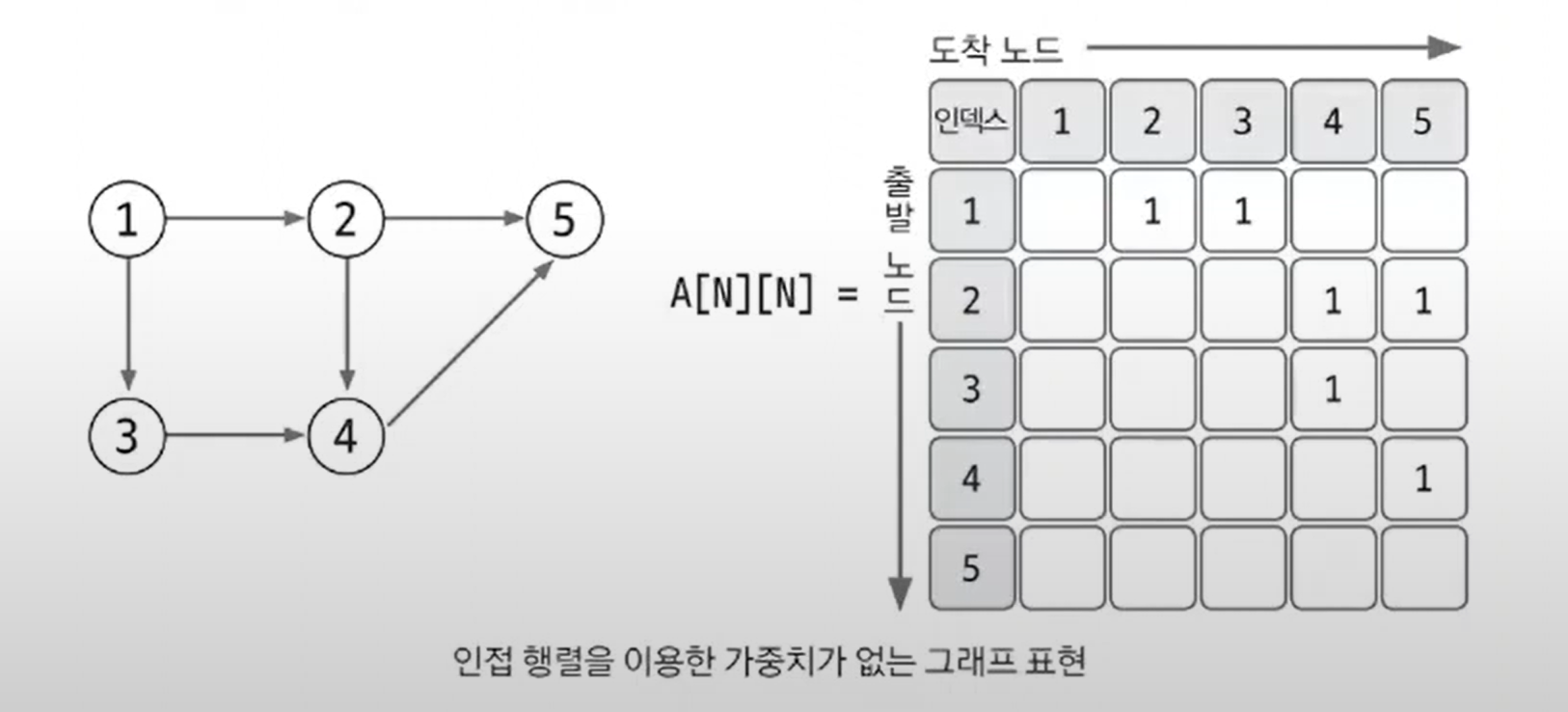
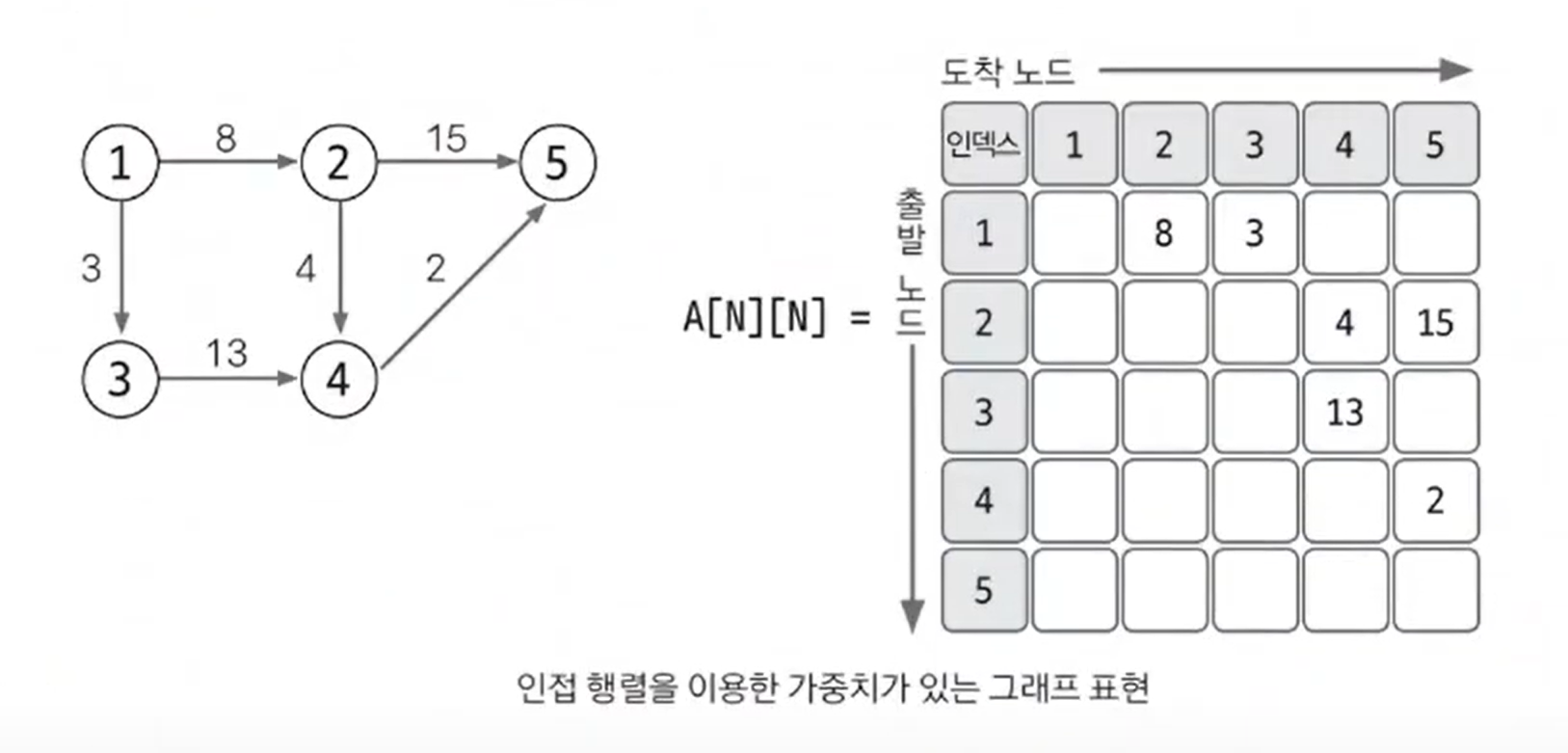
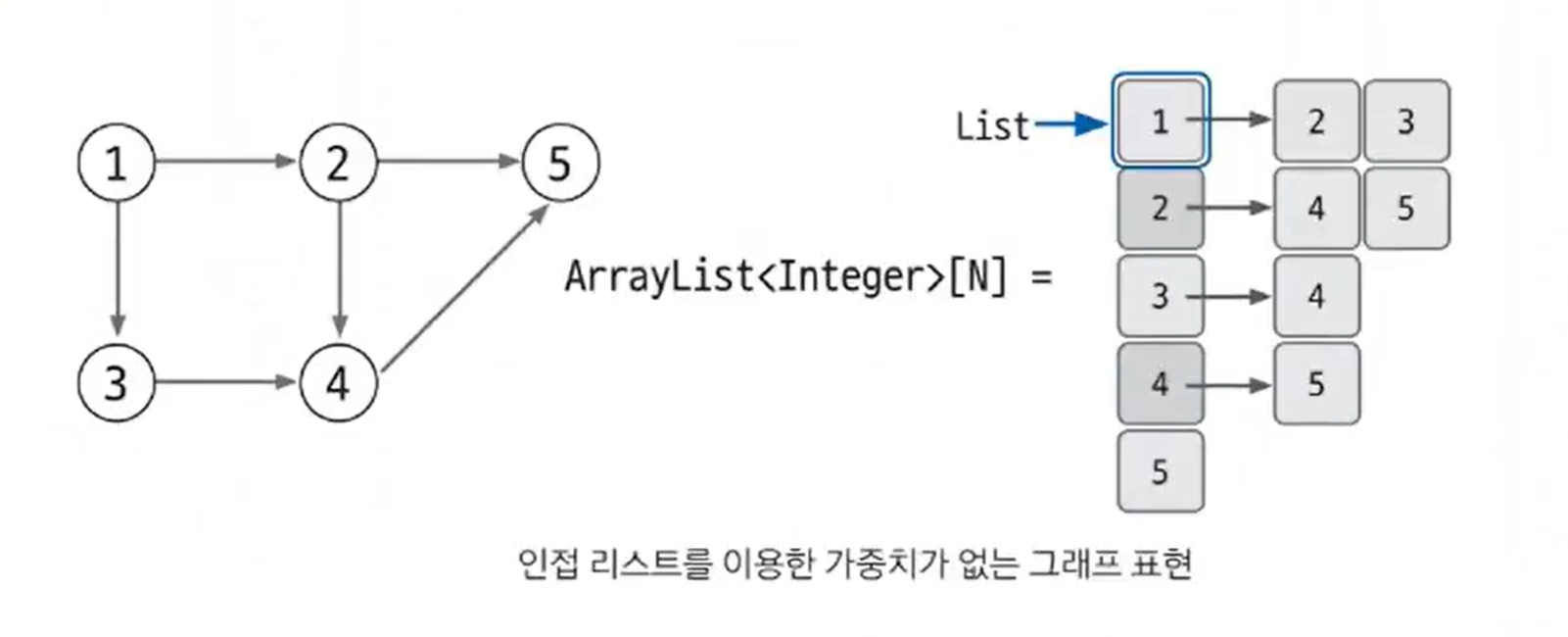
그래프의 표현

• 에지리스트
  
  

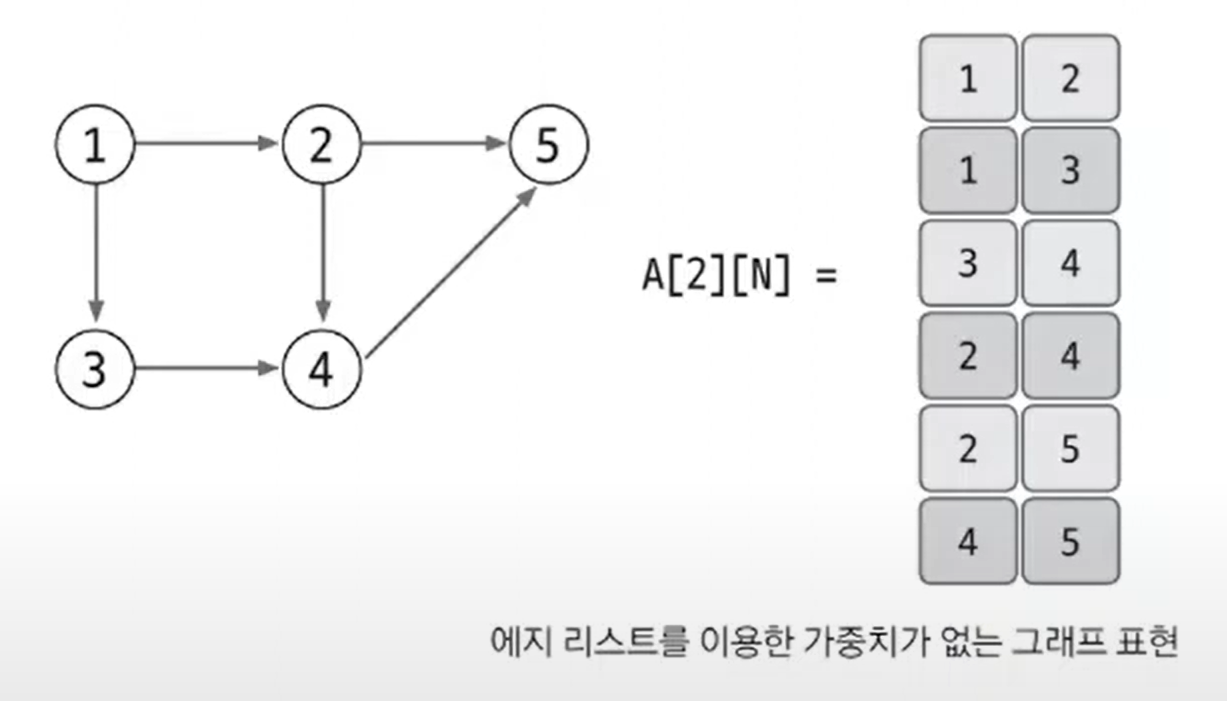
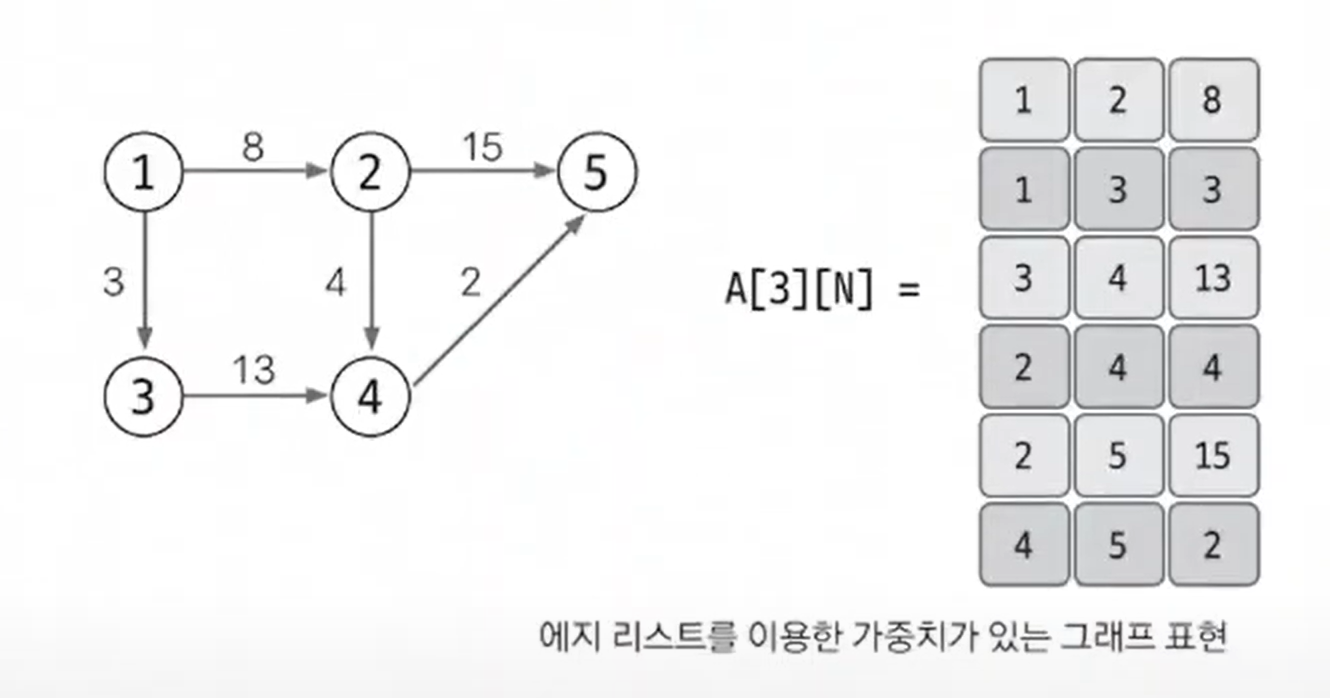
• 인접행렬

• 인접리스트

★★★

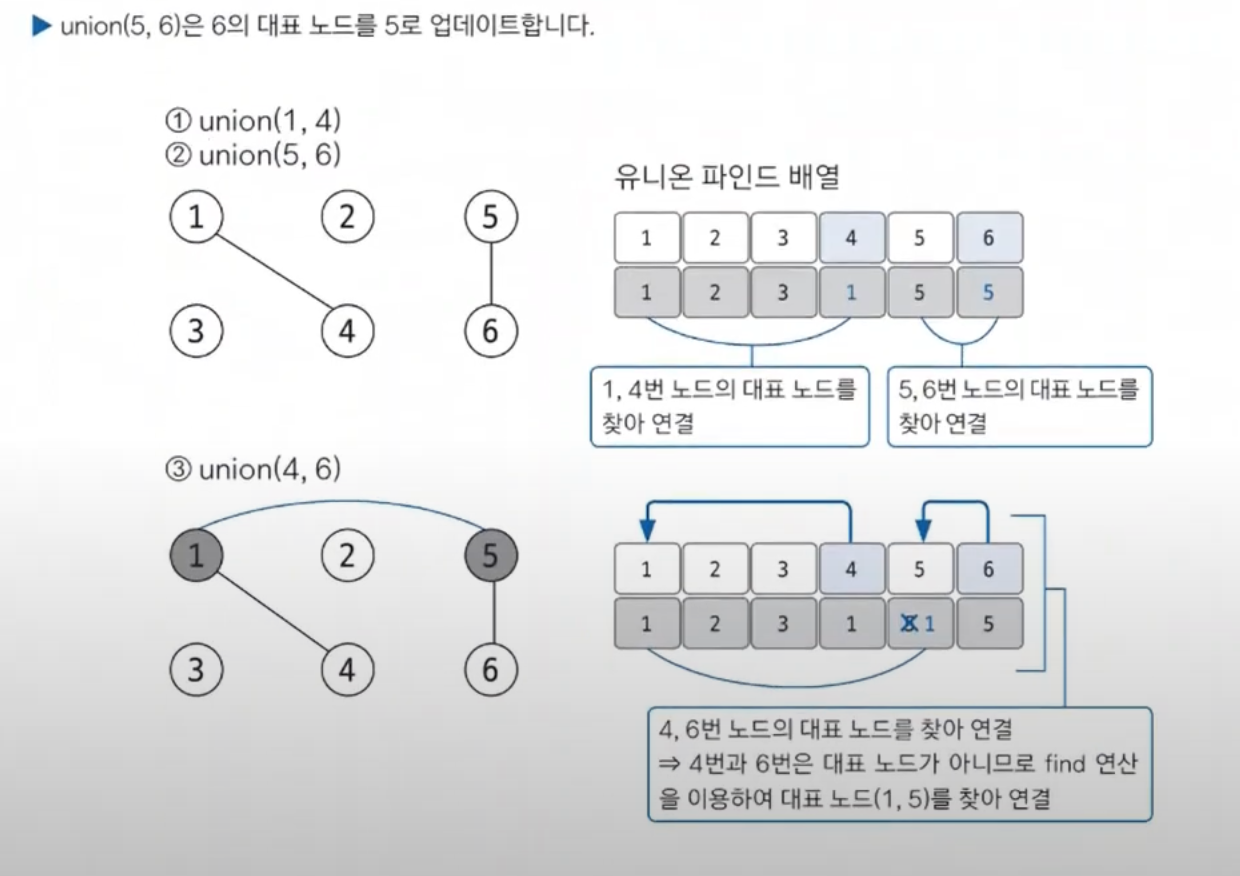
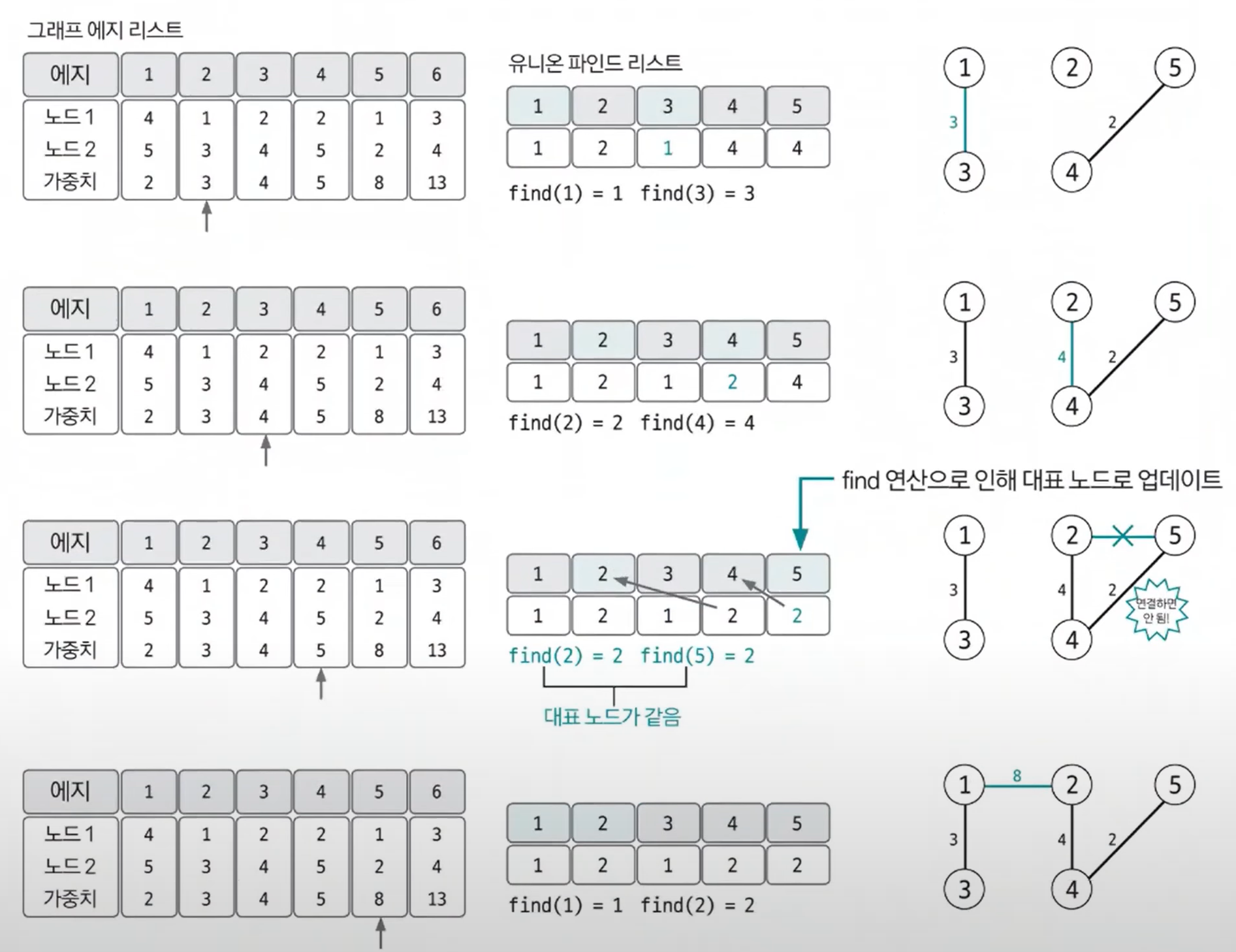
유니온 파인드

특정 노드 두개연결하는 union연산과 두노드가 같은집합에 속해있는지 확인하는 find연산으로 구성

• union 연산은 항상 대표노드끼리 연결해준다.
  

• find : 자신의 대표 노드를 찾는연산 -> 그래프를 정돈하고 시간복잡도 향상

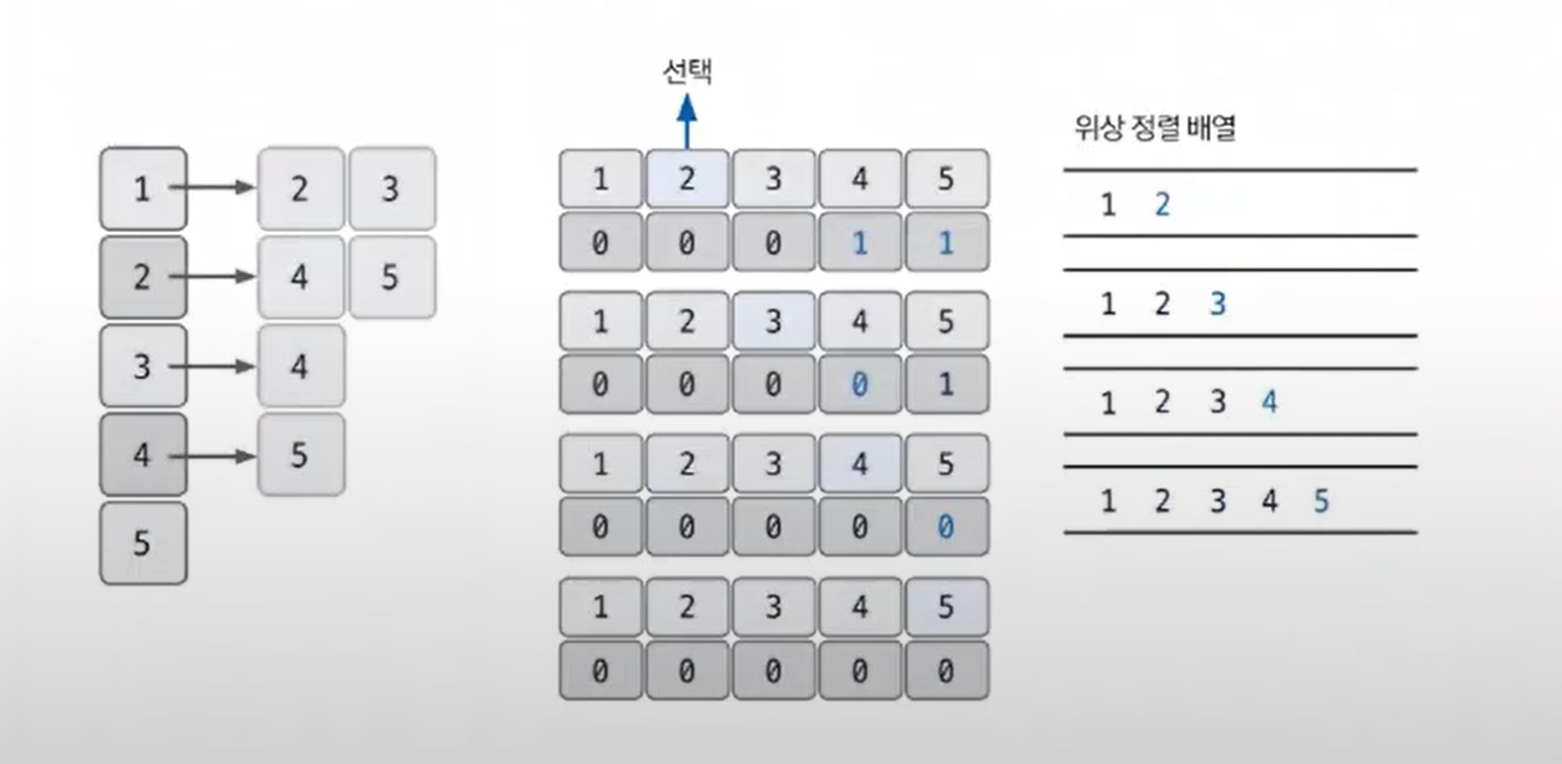
위상정렬

방향성이 있고, 사이클이 없는 그래프(DAG 그래프)에서 노드 순서를 찾는 알고리즘

다익스트라

그래프 최단거리를 구하는 알고리즘 (에지가 모두 양수여야함)

벨만포드

그래프 최단거리를 구하는 알고리즘 (음수간선도 가능)

• 사이클의 존재여부 판단가능
• 에지리스트로 구현

플로이드 워셜

• 그래프 최단거리를 구하는 알고리즘 (음수간선도 가능)

최소신장트리(MST)

• 그래프에서 모든 노드를 연결할때 가중치의 합을 최소로하는 트리
• 크루스칼 알고리즘
• 사이클을 포함하지않음(사이클이 있으면 최소가 될 수 없기때문에)
• 에지의 개수는 항상 노드(N) - 1

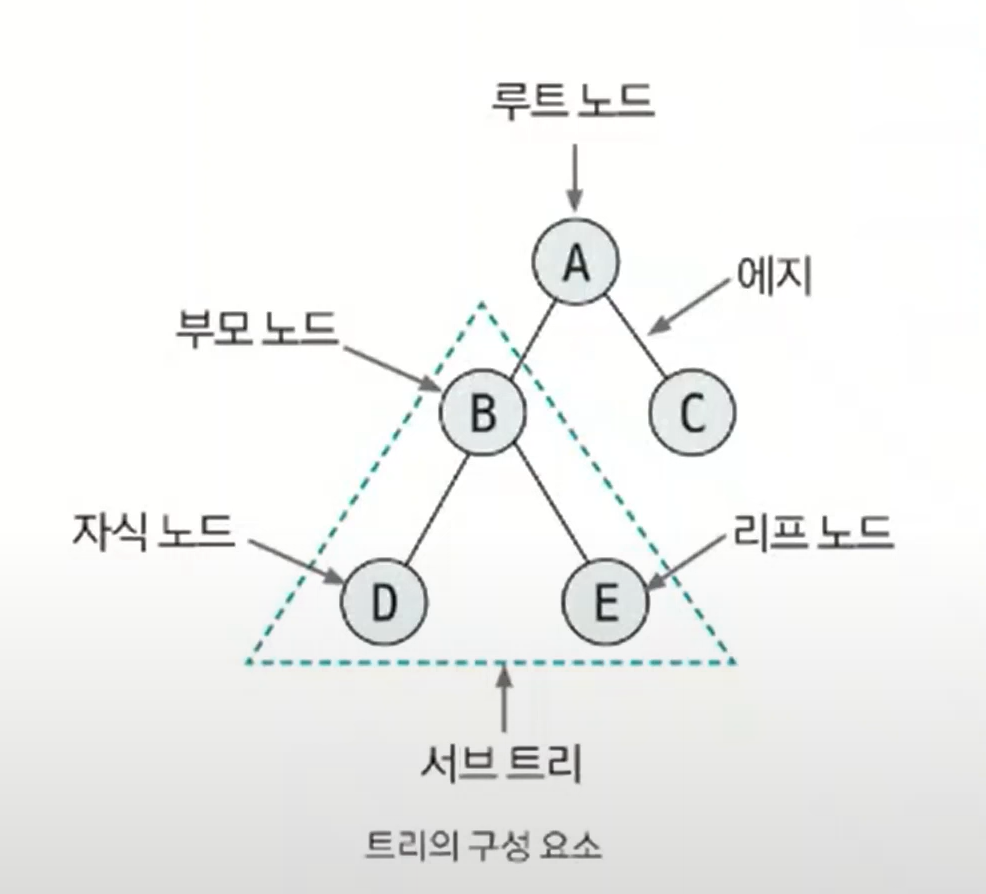
트리

그래프의 특수한 형태

• 1개의 루트노드 ( 싸이클x )

• 루트노드를 제외한 나머지는 모두 1개의 부모노드를 갖습니다

• 트리에서 임의의 두 노드를 이어주는 경로는 한개로 유일하다
  

• 그래프로 푸는 트리

  1. 인접리스트로 표현
  2. DFS / BFS

• 이진트리 / 세그먼트트리(index tree) / 최소 공통 조상 (LCA)

  1. 1차원 배열로 트리 표현
  2. 부모노드로 이동 (index / 2)
  3. 자식노드로 이동 (index 2 || index 2 + 1)

이진트리

자식 노드의 개수가 2개이하로 구성된 트리

• 배열로 표현

동적계획법 (DP)

복잡한 문제를 분리

• 한번만 계산해서 DP테이블에저장 재사용 (메모이제이션)
• 피보나치 수열 (D[N] = D[N-1] + D[N-2])