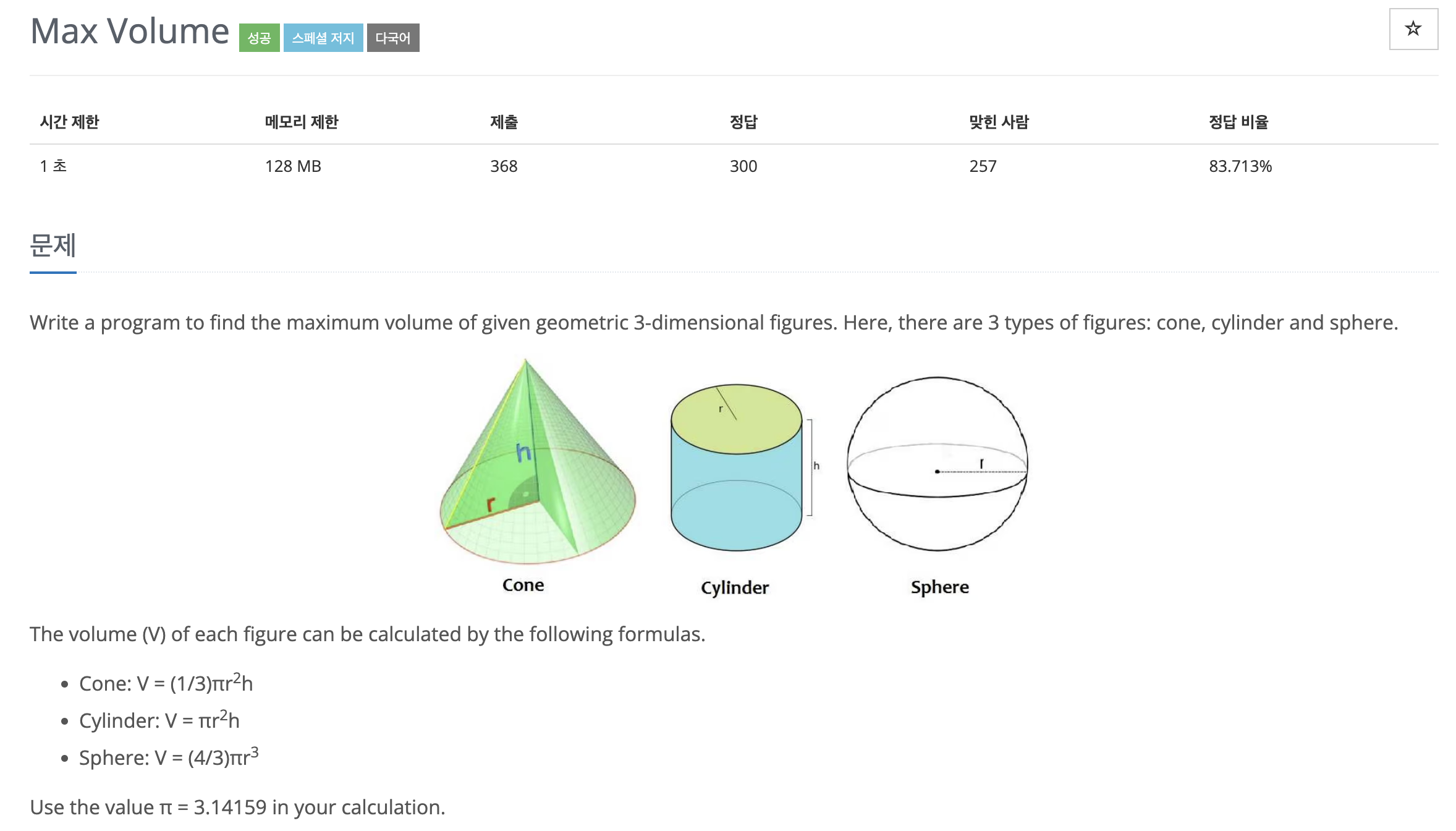
부피 계산 공식 문제 / 구현 / 실수 조심
📘 문제 설명
3차원 도형(구, 원뿔, 원기둥)의 부피를 각각 계산한 후,
가장 큰 부피를 소수점 셋째 자리까지 출력하는 문제이다.
🔹 입력 형식
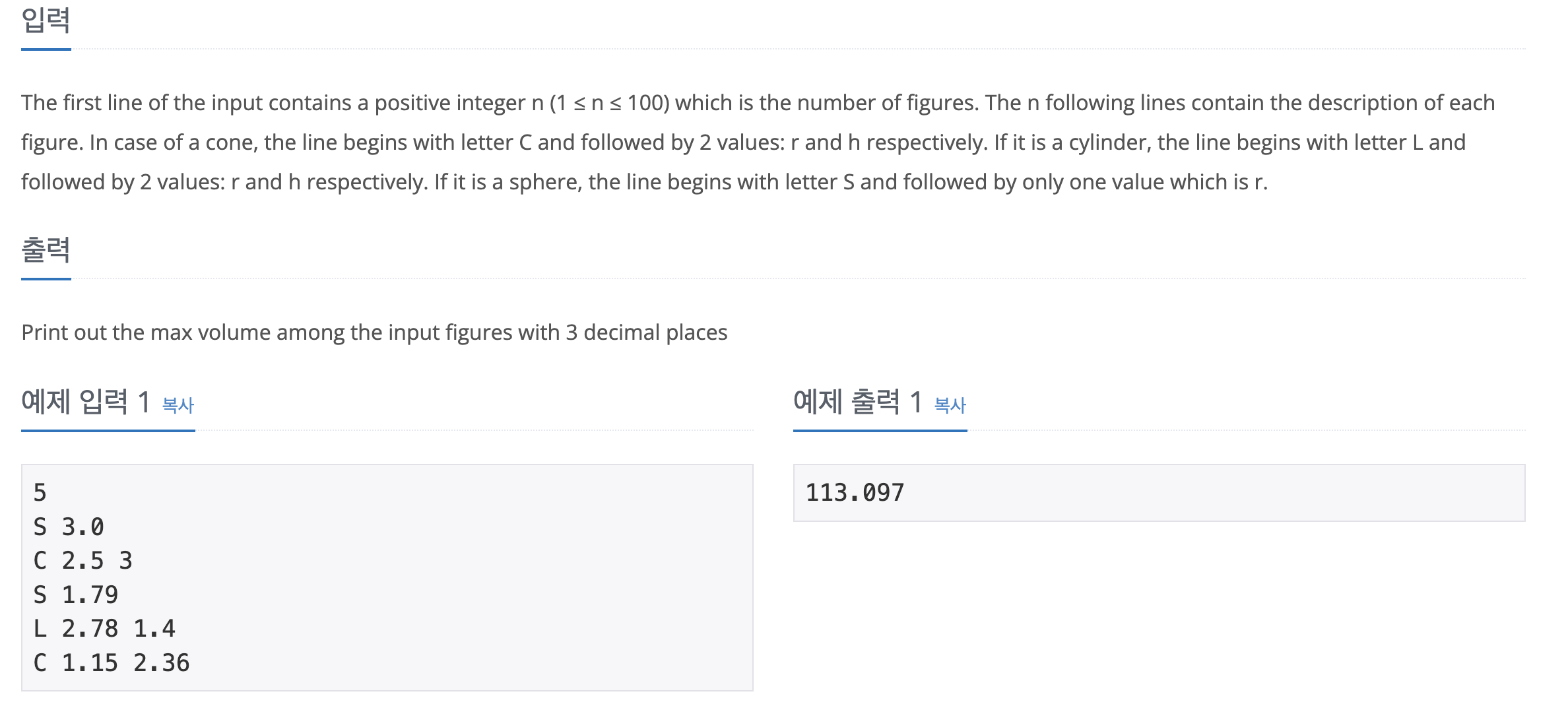
- 첫 줄: 도형의 개수
n (1 ≤ n ≤ 100) - 이후
n줄:S r: 구 (Sphere)C r h: 원뿔 (Cone)L r h: 원기둥 (Cylinder)
🔹 출력 형식
- 가장 큰 부피를 소수점 셋째 자리까지 출력
주의 ⚠️
math.pi 대신 π = 3.14159 고정 사용해야 정답 처리된다.
📌 도형별 부피 공식
| 도형 | 공식 |
|---|---|
| 구 (Sphere) | (4/3) × π × r³ |
| 원기둥 (L) | π × r² × h |
| 원뿔 (C) | (1/3) × π × r² × h |
문제 접근 💡
- 입력을 split()으로 받아 도형을 판별하고
- 조건문으로 부피 계산 후 max_volume에 저장
- 마지막에 소수점 셋째 자리까지 출력
🧾 풀이 코드 (Python)
PI = 3.14159
n = int(input())
max_volume = 0
for _ in range(n):
data = input().split()
shape = data[0]
if shape == 'S':
r = float(data[1])
volume = (4/3) * PI * r**3
elif shape == 'L':
r, h = map(float, data[1:])
volume = PI * r**2 * h
elif shape == 'C':
r, h = map(float, data[1:])
volume = (1/3) * PI * r**2 * h
max_volume = max(max_volume, volume)
print(f"{max_volume:.3f}")
