얼마 전, 파이썬으로 개발을 하던 중 csv 파일에서 import 해온 특정 카테고리를 분류하는 작업을 진행하다가 효율적인 자료구조가 매우 중요함을 깨닫는 시기가 있었다.
본론으로 바로 들어가보자,
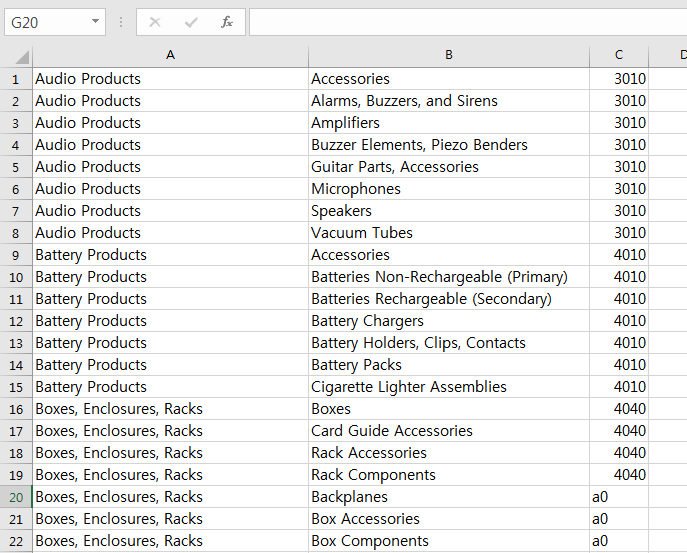
위 사진은 A, B, C 총 세개의 열이 존재하는 엑셀파일의 내용이다.
A열은 대분류,
B열은 소분류,
C열은 상품코드
총 3가지 카테고리로 구분이 되어있고 대분류의 갯수가 소분류의 갯수보다 작다.
이제 우리는 다른 사이트에서 대분류와 소분류 즉 A열과 B열에 해당하는 내용을 순서없이 크롤링해서 가져올것이다.
예를들어 한번에 가져오는 데이터가
(Audio Products, Speakers)이런식이면
이 때 가져온 내용과 엑셀의 A열과 B열 데이터를 매치시켜 C에 해당하는 값을 찾아야 하며,
A, B 의 데이터에 대한 C열의 매치 값은 N개가 될 수 있다.
방금 든 예시로 본다면 데이터 (Audio Products, Speakers)에 대한 C열의 상품코드는 3010가 되는것이다. (물론 사진엔 안나와있지만 저 데이터와 매치되는 상품코드가 더 있을 수 있다)
이제 생각해보자.
a, b, c 가 A, B, C열에 대한 하위 항목이라고 했을 때,
우리가 가져온 a, b 값으로 c를 찾기위해 어떤 자료구조를 사용할 것인가 ?
처음에 본인은 엑셀파일을 import 해온 뒤 다음과 같은 방법을 사용하려고 했다.
category_list = [
['Audio Products', 'Accessories', '3010'],
['Audio Products', 'Alarms, Buzzers, and Sirens', '3010'],
['Audio Products', 'Amplifiers', '3010']...]
for cat in category_list:
a, b, c = cat
if a, b == 'a', 'b':
return c이 방법이 꽤 직관적이고 괜찮다고 생각했지만,
- 첫 번째로
category_list안의 요소가 수천개라는 것을 간과했다. - 두 번째로
a와b에 해당하는c값이 여러개일 수도 있다는 것을 간과했다.
이렇게 되면 하나의 a, b 쌍에 해당하는 c를 찾으려고 시도할 때마다 수천번의 for문을 돌아야 한다.
즉, 엑셀을 매번 처음부터 끝까지 전부 다 읽어야 한다.
여기까지가 실리콘밸리의 개발자 친구와 이야기를 하기 전 마주한 문제다.
문제를 설명하고 난 뒤 친구는:
어떻게 해야 O(n)이 아니라 O(1)을 만들 수 있을까?
Dict는 N메모리를 사용해서 O(1)을 만들 수 있는 좋은 구조..
파이썬에서 dictionary는 Key와 Value를 저장할 때 메모리 위치 index값과 같이 저장하기 때문에, Key값으로 Value값을 바로 구할 수 있다.
따라서 다음과 같은 방법을 생각해냈다.
a, b를 Key로 하는 dict, 즉(a, b)tuple 값을 Key로 가지는 dict
-->{(a, b): [c, ...], ...}- a, b가 중첩된 dict
-->{a: {b: [c, ...], ...}, ...}
다행히 처음 생각해냈던 수천번의 for문을 돌린다는 생각에서는 벗어났지만,
두가지 방법 중 어떤 방법을 선택해야 할지 감이 안왔다.
다시 친구에게 물어본 결과, 다음 두가지를 수식으로 표기해 보라고 했다.
N개 row가 있다고할때
1. 튜플로 했을 때와dict[(a,b)] = c
2. 2차 dict로 했을 때dict[a][b] = c
- 메모리 사용량 (공간 복잡도)
- 검색 시 c를 찾기위한 루프 횟수 (시간 복잡도)
그래서 해봤다.
메모리 사용량 구하기(공간 복잡도)
Key 값의 사이즈를 생략한 대략적인 메모리 사용량을 계산해보자
a의 갯수는 (A열(대분류) 행의 갯수) M으로 표기
b의 갯수는 (B열(소분류) 행의 갯수) N으로 표기
한다고 했을 때
1번 case 의 메모리 사용량 : N
--> 왜냐면 해당 dict의 Key 갯수는 b의 전체 갯수와 똑같기 때문이다.
2번 case 의 메모리 사용량 : M + N
--> 왜냐면 Key의 갯수는 바깥쪽(1차) Key 갯수는 a와 같기 때문에 M개,
안쪽(2차) Key 갯수는 b의 갯수와 같기 때문에 N개이기 때문이다.
위 수식만으로는 부족하다. 실제 a와 b의 사이즈를 포함시키지 않았기 때문이다.
이제 위 수식을 조금 더 구체화 시키기 위해,
Key 값의 사이즈를 고려한 메모리 사용량을 구해보자
여기서는 a와 b의 사이즈를 각각 a'와 b' 로 가정해보자.
1번 case 의 Key 값 사이즈를 고려한 메모리 사용량 : (a'+ b') * N
--> 튜플에서 a와 b의 사이즈의 합은 a'+b', 여기에 dict Key의 갯수 N개만큼 곱해야 하기 때문이다.
2번 case 의 Key 값 사이즈를 고려한 메모리 사용량 : (a' * M) + (b' * N)
--> 1차 Key와 2차 Key를 나누어서 생각해보면,
- 1차 Key 값의 갯수(
M)에 a의 사이즈(a')를 곱한 만큼의 크기와a' * M - 2차 Key 값의 갯수(
N)에 b의 사이즈(b')를 곱한 만큼의 크기를 더해야 하기 때문b' * N
1, 2번 케이스 수식을 비교해보면
(a' * N) + (b' * N) 과 (a' * M) + (b' * N) 이다.
여기서 (b' * N)은 공통적으로 있는 부분이니 (a' * N)과 (a' * M) 의 크기를 비교하려면,
M과 N을 비교하면 된다.
이때 대분류의 갯수가 소분류의 갯수보다 작기 때문에 M < N,
즉 2번 case 의 메모리 사용량이 더 작다고 말할 수 있다.
검색 시 루프 횟수 구하기(시간 복잡도)
이제 검색 시 루프 횟수를 알아보자.
참고로 위에 본인이 작성한 코드에서는 루프 횟수가 N번이다.
for cat in category_list:
a, b, c = cat
if a, b == 'a', 'b':
return ccategory_list 의 요소 갯수(N)에 따라 루프 횟수가 결정되기 때문이다.
1번 case의 루프 횟수는 1번이다. (1차 Key loop 한번)
2번 case의 루프 횟수는 2번이다. (1, 2차 Key loop 각각 한번)
상수 횟수는 무시할 만한 수준이기에 고려하지 않아도 된다.
결론
시간복잡도가 1, 2번 case 모두 상수횟수로 고려하지 않아도 된다면,
공간복잡도를 계산해봤을 때 2번 case의 메모리 사용량이 더 적다.
물론, 저 이외에도 고려할 사항들이 충분히 더 많을 수도 있지만
우선적으로 두가지만 고려해보면 2번 case를 사용하는 것이 합리적일 것이다.
이번 경험을 통해서 그냥 생각나는대로 자료구조를 설계하는 것이 아니라
최소한 스스로 이런 과정을 거쳐야지만 나중에 누군가와 프로젝트를 진행할 때
문제에 대해 논의가 가능하다는 것을 느꼈다.
그래서 요약하자면
효율적인 구조를 설계하기 위해서는 시공간 복잡도를 수식으로 나타내고 계산해보는 과정을 거쳐보아야 한다.
