TIL - 2024/03/25

정렬

셸 정렬 → O(n^1.25)

단순 삽입 정렬의 단점을 보완하여 더 빠르게 정렬 가능한 정렬 방식

단순 삽입 정렬은 정렬이 되어있을수록 정렬 속도가 빠르지만 삽입할 위치가 멀면 이동횟수가 많아진다는 단점이 있다.

셸 정렬은 정렬할 배열의 원소를 그룹으로 나누어 각그룹별 정렬을 수행한다. 이후 그룹을 합치는 과정을 통해 이동 횟수를 줄인다.

예)

8개의 숫자를 정렬한다고 할때, 각 수를 n//2 만큼 떨어져 있는 수들과 반복하여 비교, 정렬한다. n // 2가 1이 되었을 때, 단순 삽입 정렬을 1번 수행해서 정렬을 완료할 수 있다.

def shell_sort(arr):
	n = len(arr)
	h = n // 2

	while h > 0:
		for i in range(h, n):
    	j =  i - h
    	temp = arr[j]
    			
    	while j >= 0 and a[j] > tmp:
    		a[j + h] = a[j]
    		j -= h
    	
    	a[j + h] = tmp
    	h //= 2

셸 정렬에서는 h 값을 지정하는 것이 중요하다. 위 예시처럼 h 값이 배수로 이루어져있으면(h: 4 → 2 → 1) 값이 적절하게 섞이지 않아 큰 성능 향상을 기대하기 힘들다.

그래서 h 값을 h = (h - 1) // 3 처럼 사용하면 보다 큰 효과를 얻을 수 있다.

퀵 정렬 → O(nlogn) , O(n^2)

퀵 정렬은 가장 빠른 정렬 알고리즘으로 널리 사용되고 있다.

기본 정렬 방식

피벗(pivot)이라는 그룹을 나누는 기준을 잡고 두 그룹으로 나누어 정렬이 진행된다.

양쪽 (pr, pl)에서 피벗을 향해 인덱스를 바꿔가며 순회하며 크기를 비교하여 큰 값이 피벗 오른쪽으로, 작은 값이 피벗 왼쪽으로 오게끔 정렬한다.

배열 순회는 양쪽 인덱스의 값이 교차되는 순간 종료된다.

# 피벗을 기준으로 두 그룹으로 나누기
def partition(arr):
	n = len(a)
	pl = 0
	pr = n - 1
	pivot = arr[n // 2]

	while pl <= pr:
		while arr[pl] < pivot : pl += 1
		while arr[pr] > pivot : pr -= 1
		if pl <= pr:
			arr[pl], arr[pr] = arr[pr], arr[pl]
    		pl += 1
        	pr -= 1	        

퀵 정렬도 분할 정복 알고리즘에 기원해서 하나의 원소만 가지는 그룹이 될때 까지 나누어서 정렬을 수행하게 된다.

def qsort(arr, left, right):
	pl = left
	pr = right
	pivot = arr[(left + right) // 2]

	while pl <= pr:
		while arr[pl] < x : pl += 1
    	while arr[pr] > x : pr -= 1
    	if pl <= pr:
    		arr[pl], arr[pr] = arr[pr], arr[pl]
        	pl += 1
        	pr += 1
        		
        	
	if left < pr: qsort(arr, left, pr)
	if right > pr: qsort(arr, pl, right)
        	

퀵 정렬의 경우 서로 이웃하지 않은 요소끼리 교환이 이루어지기 때문에 안정적이지 않은 알고리즘이다.

피벗 선택하기

퀵 정렬은 피벗을 어떤 값으로 선택하느냐에 따라 나뉘는 배열과 정렬 성능에 차이가 생긴다.
맨 앞의 값을 사용하면 한쪽으로 치우쳐져 정렬을 반복하기 때문에 이상적인 성능을 기대하기 힘들다.
가운데 값을 사용했을 떄 절반 크기의 그룹으로 나누어 이상적인 성능으로 사용할 수 있지만 가운데 값을 구하는 과정에서 계산 시간이 소모된다는 단점이 있다.

• 원소의 수가 3이상이면, 배열에서 임의 원소 3개를 꺼내 중앙 값을 피벗으로 선택한다.
• 나누어야할 배열의 맨 앞, 맨 뒤, 가운데 원소를 먼저 정렬하고 가운데 값과 맨 끝에서 두번째 원소(arr[-2]) 원소의 위치를 교환한다. 이 때 맨 끝에서 두번째 값이 피벗이되고, 나눌 대상을 arr[left -1:right - 1]로 제한 할 수 있다.
  

시간 복잡도

일반적인 상황에서는 문제를 작은 단위로 나눠 해결하기 때문에 O(nlogn)이지만, 피벗값을 선택하는 방법에 따라 실행도가 달라져 최악의 경우 O(n^2)까지 지연될 수 있다.

병합 정렬 → O(nlogn)

배열의 앞부분과 뒷부분의 두 그룹으로 나누어서 정렬한 후 기준에 따라 병합하는 과정을 반복하는 알고리즘

def merging_sort(arr, left, right):
    n = len(arr)
    center = (left + right) // 2
    
    # center를 기준으로 양 배열을 합병정렬 -> 재귀를 통한 분할 정복
    merging_sort(arr, left, center)
    merging_sort(arr, center + 1, right)
    
    buffer_inject_index = buffer_search_index = 0
    arr_search_index = arr_inject_index = left
    
    # buffer에 정렬된 앞부분 배열 삽입
    while buffer_inject_index <= center:
        buffer[buffer_inject_index] = arr[arr_search_index]
        buffer_inject_index += 1
    	arr_search_index += 1
        
	 # buffer와 정렬된 뒷부분 배열의 원소를 비교하며 정렬
	 while arr_search_index <= right and buffer_search_index < buffer_inject_index:
        if buffer[buffer_search_index] <= arr[arr_search_index]:
            arr[arr_inject_index] = buffer[buffer_search_index]
            buffer_search_index += 1
        else:
            arr[arr_inject_index] = arr[arr_search_index]
            arr_search_index += 1
    
        arr[arr_inject_index] += 1
    
	## buffer가 남아있는 경우 배열의 뒷부분에 병합
    while buffer_search_index < buffer_inject_index:
        arr[arr_inject_index] = buffer[buffer_search_index]
        arr_inject_index += 1
        buffer_search_index += 1

병합 정렬의 시간 복잡도는 O(nlogn)이다. 병합 정렬은 원소간 위치를 교환하는 것이 아니기 때문에 안정적이다.

힙 정렬 → O(nlogn)

‘부모의 값이 자식 보다 항상 크다.(or 항상 작다)’는 조건을 만족하는 최대 힙의 규칙을 만족하는 완전 이진 트리를 통해 정렬하는 알고리즘

힙 정렬 규칙

• 힙에서 최대값인 루트를 꺼낸다.
• 힙의 마지막 원소를 루트로 이동시킨다.
• 다시 힙이 되도록 위치를 이동시킨다.
  

def heap_sort(arr, left, right):
    def down_heap(arr, left, right):
        temp = arr[left]
        parent = left
    
    	while parent < (right + 1) // 2 :
	        cl = parent * 2 + 1
            cr = cl + 1
   			child = cr if cr <= right and a[cr] > a[cl] else cl
                
            if temp >= child:
                break
                
            a[parent] = a[child]
            parent = child
    
        a[parent] = temp
    
        n = len(arr)
    
	for i in range((n - 1)//2, -1, -1): # a[i] ~ a[n-1] 힙 구조 만들기
    	down_heap(arr, i, n - 1)
    
	for i in range(n-1, 0, -1): 
    	a[0], a[i] = a[i], a[0] # 루트 노드의 값과 힙의 제일 작은 값과 위치 변경
		down_heap(arr, 0, i - 1) # 힙 만들기
    
	return arr

힙 구조를 만드는 시간 복잡도가 O(logn)이므로, 배열을 순회하면서 힙 정렬을 통해 정렬하는데 걸리는 시간 복잡도는 O(nlogn)이다.

collections.deque()

• deque.append(n)
• deque.appedleft(n)
• deque.pop()
• deque.popleft()
• deque.extend(array) → 주어진 배열을 순회하면서 deque의 오른쪽에 추가한다.
• deque.extednleft(array) → 주어진 배열을 순회하면서 deque의 왼쪽에 추가한다.
• deque.remove(item) → 특정 item을 찾아 제거한다.
• deque.rotate(n) → n 만큼 deque를 회전시킨다. ( 양수인 경우 오른쪽, 음수면 왼쪽 )

우선순위 큐 (Priority Queue)

일반적으로 먼저 들어온 데이터가 먼저나가는 큐형식과 달리 높은 우선순위의 데이터가 먼저 나가는 큐를 의미한다.

우선순위 큐의 경우 힙(heap)으로 구현한다.

힙 (Heap)

힙은 완전 이진트리 형태의 자료구조를 말하며 마지막 레벨을 제외하고 모든 레벨이 모두 채워져 있어야하며 마지막 레벨의 경우 왼쪽부터 채워져 있어야한다.

• 최대 힙 ( Max Heap ) ⇒ 부모 노드의 키 값이 자식 노드보다 큰 구조
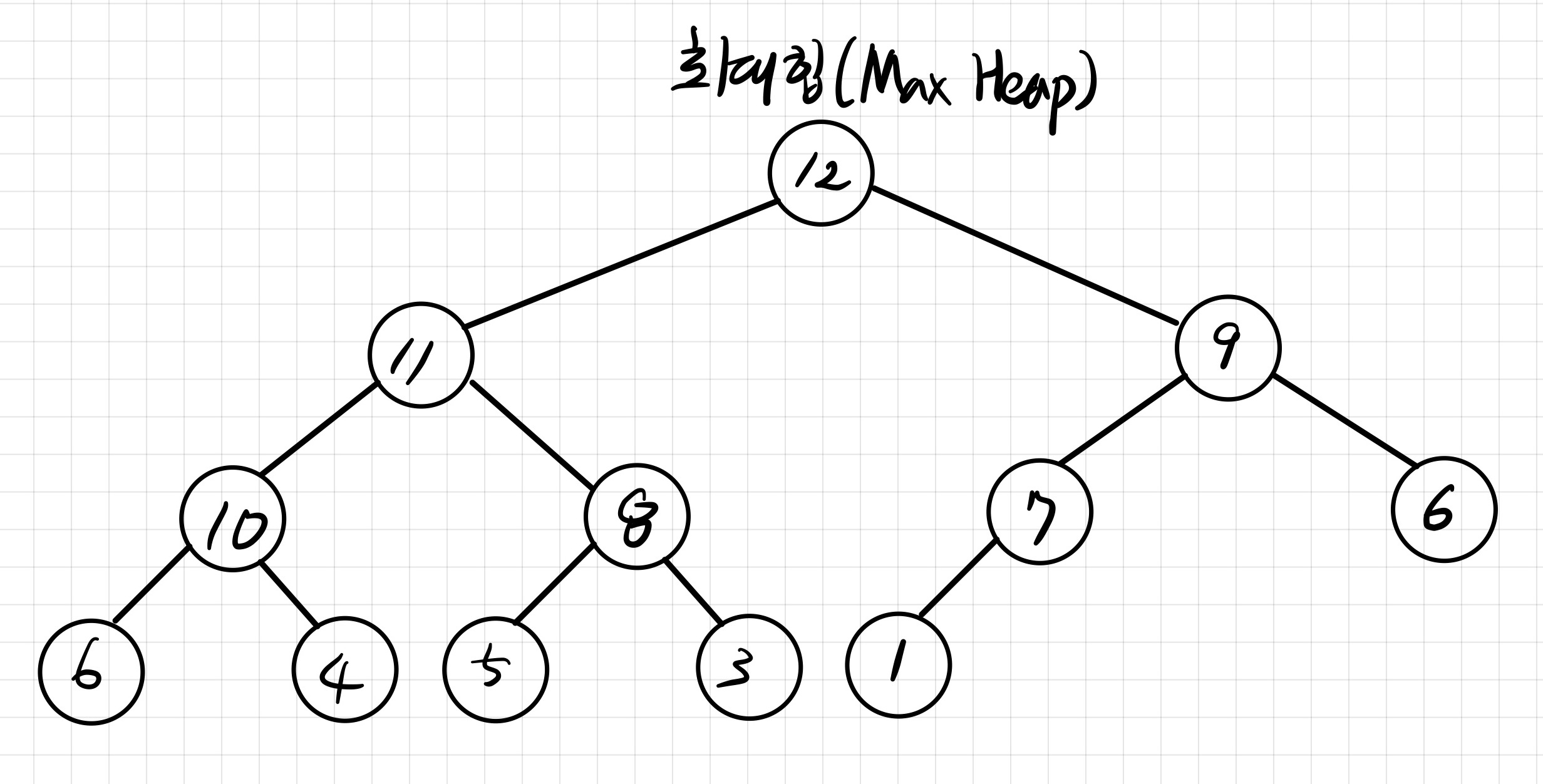
• 최소 힙 ( Min Heap ) ⇒ 부모 노드의 키 값이 자식 노드보다 작은 구조

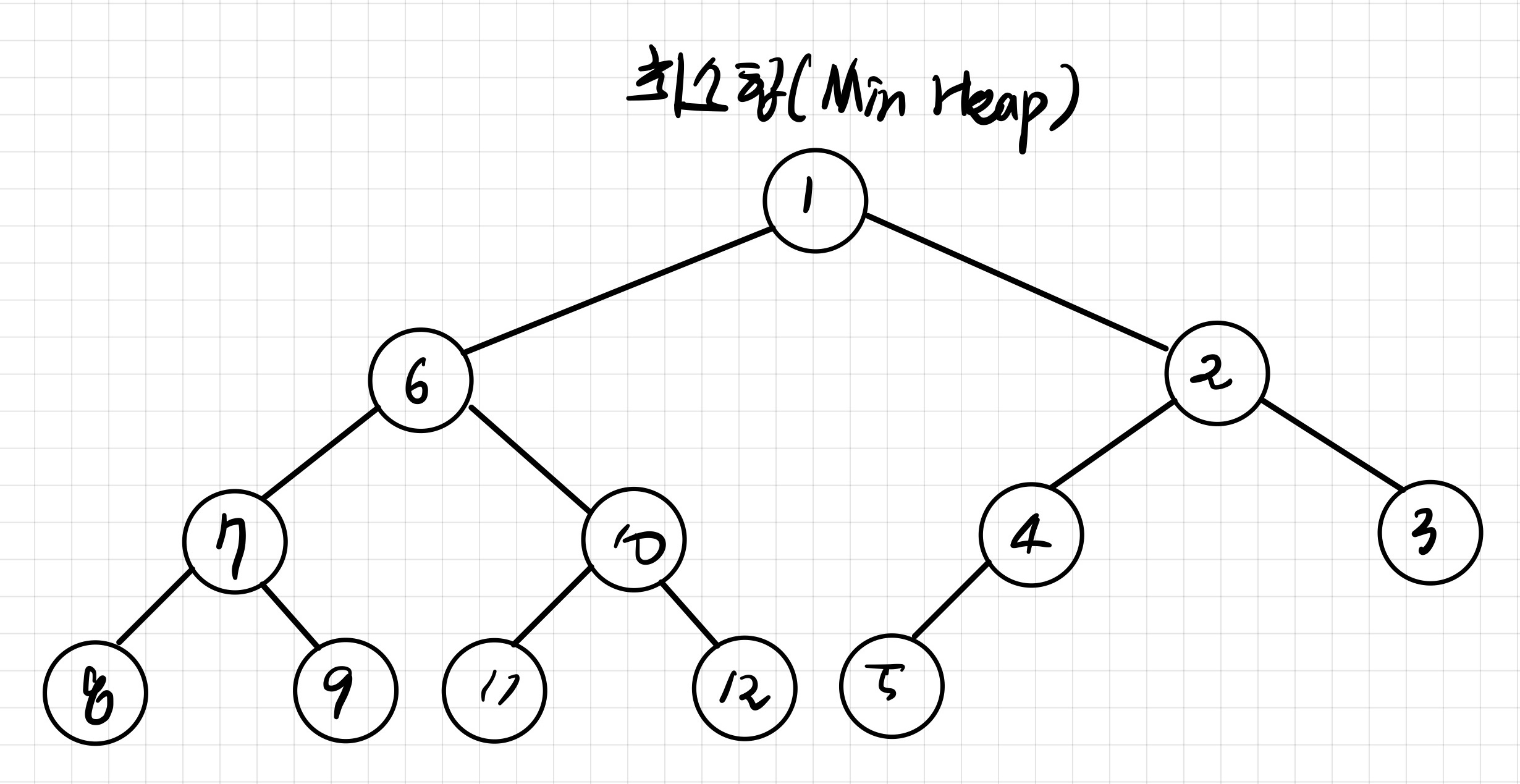
힙을 배열로 표현하기

• 왼쪽 자식 노드 → 부모 노드 index * 2
• 오른쪽 자식 노드 → 부모 노드 index * 2 + 1
• 부모 노드의 인덱스 → 자식 노드 (왼/오) // 2

priority queue vs heap queue

우선 순위 큐의 경우 Thread-Safe하고, 힙 큐의 경우 non-safe하다 정렬에 이써서 안정성을 추구해야하는 경우 우선순위 큐를 활용하고, 일반적으로는 heapq를 사용하자.

우선순위 큐의 내부 구현으로도 heapq를 사용한다. 우선순위 큐 라이브러리인 PriorityQueue()는 멀티 스레드 환경에서 현재 스레드에서 작업하는 내용이 다른 스레드로 부터 안전하다는 점을 보장하는 ‘Thead-safe’를 확인하는 과정이 포함되어 있기 때문에 heapq 보다 느리게 동작한다.

heapq로 최소힙/최대힙 구현

heapq 모듈 자체가 최소 힙을 구현하도록 만들어져있기 때문에 특별한 추가 구현이 필요없다.

하지만 heapq 모듈을 최대 힙을 사용하기 위해서는 약간의 데이터 조작이 필요하다.

# Max Heap

N = int(sys.stdin.readline())
numbers = [ int(sys.stdin.readline()) for _ in range(N) ]

hq = []

for n in number:
  match n:
    case 0:
      if len(hq) == 0:
        print(0)
      else:
        print(heapq.heappop(hq)[1])
    case _:
      heapq.heappush(hq, [n * -1, n])

heapq로 배열에 데이터를 넣을 때 튜플이나 리스트 형태로 놓고, 0번째 index의 값을 해당 값의 음수값을 넣어서 저장하면 0 번째 인덱스를 기준으로 최소 힙으로 삽입하기 때문에 최대 힙처럼 동작하도록 구현할 수 있다.

해시 테이블 (Hash Table)

key, value 구조를 통해 원하는 값을 빠르게 검색할 수 있는 방법.

해시 테이블은 각각의 Key 값에 대해서 해시함수(Hash Function)를 적용해 고유한 index를 생성하고 내부 배열의 인덱스와 비교하여 데이터를 저장한다.

해시 테이블의 경우 같은 키에 대해서 항상 같은 값을 보내주기 때문에 시간 복잡도는 O(1)이라고 볼 수 있다.

해시 충돌(Collision)

해시 함수에 의해서 생성된 키와 해시값의 관계는 항상 1대1이 아니라 다대일의 관계를 가진다. 이런 현상을 충돌이라고 부르고 체인법과 오픈 주소법을 통해서 문제에 대처할 수 있다.

• 체인법: 해시값이 같은 원소를 연결 리스트로 관리한다.
• 오픈 주소법: 빈 버킷을 찾을 때 까지 해시를 반복시킨다.

체인법(Open Hashing)

해시값이 같은 데이터를 체인 모양의 연결리스트로 연결하는 방법을 말하며 오픈 해시법이라고도 한다

# Node Class
class Node:
	def __init__(self, key: Any, value: Any, next: Node) -> None:
		self.key = key
		self.value = value
		self.next = next

class ChainedHash:
	def __init__(self, capacity):
		self.capacity = capacity
		self.table = [ None ] * self.capacity
		
	def hash_value(self, key: Any) -> int:
		if isinstance(key, int):
			return key % self.capacity
			
		return (int(hashlib.sha256(str(key).encode()).hexdigest(), 16) % self.capacity)
		

def search(self, key) -> Any:
	hash = self.hash_value(key)
	p = self.table[hash]
	
	while p is not None:
		if p.key == key:
			return p.value
		
		p = p.next
		
	
	return None

• 검색
  • 해시 함수를 통해 키를 해시값으로 변환한다.
  • 해시 값을 인덱스로하는 버킷을 바라본다.
  • 버킷이 참조하는 링크드리스트를 맨 앞부터 스캔해서 원하는 값이 발견되면 탐색을 마치고, 원하는 값을 찾지 못한채 링크드리스트가 종료되면 실패를 반환한다.

def add(self, key, value) -> bool:
	hash = self.hash_value(key)
	p = self.table[hash]
	
	while p is not None:
		if p.key = key:
			return False
		p = p.next
		
	temp = Node(key, value, self.table[hash])
	self.table[hash] = temp
	return True

• 삽입
  • 해시 함수를 통해 키를 해시값으로 변환한다.
  • 해시 값을 인덱스로 하는 버킷을 바라본다.
  • 버킷이 참조하는 링크드 리스트를 맨 앞부터 스캔해서 같은 값이 보이는 경우 추가 실패이고, 리스트의 맨 끝까지 해당 숫자가 존재하지 않으면 리스트의 맨 앞에 원소를 추가한다.

def remove(self, key) -> bool:
	hash = self.hash_value(key)
	p = self.table[hash]
	pp = None
	
	while p is not None:
		 if p.key == key:
			 if pp is None:
				 self.table[hash] = p.next:
				else:
					pp.next = p.next
			return True
			
		pp = p
		p = p.next
	return False
	

• 삭제
  • 해시 함수를 통해 키를 해시값으로 변환한다.
  • 해시 값을 인덱스로하는 버킷을 바라본다.
  • 버킷이 참조하는 링크드 리스트를 따라 삭제할 값을 발견하면 노드를 리스트에서 삭제한다. 그렇지 않으면 실패한다. 삭제하는 경우 이전 값(pp)와 다음값(p.next)를 연결함으로서 데이터를 삭제한다.

오픈 주소법( Open Addressing)

충돌이 발생하는 경우 재해시(rehashing)을 통해 버킷을 찾는 방법. 닫힌 해시법(closed hashing)이라고도 한다.

재해시 함수의 경우 자유롭게 설정이 가능하다.

• 추가
  • 해시를 통해 키를 해시값으로 변환한다.
  • 버킷에 값이 채워져있는 경우 임의로 설정한 재해시 함수를 통해 반복해서 빈버킷이 나올때 까지 재해시를 반복한다. (선형 탐사법)
• 삭제
  • 재해시를 하면서 해당 값이 나오거나(성공), 빈 버킷이 나올때(실패) 까지 반복한다.
• 검색
  • 재해시를 반복하며 해당 값이 나오는 경우 성공, 빈 버킷이 나오면 실패다.