그래프 알고리즘
그래프
에지로 연결한 추상적이고 일반적인 자료구조.
트리의 경우 사이클이 없는 그래프이고, 링크드 리스트의 경우 하나의 경로로만 이루어진 그래프이다.
용어
-
정점(vertext), 노드(node) ⇒ 어떤 대상의 객체
-
에지(Edge), 링크(Link) ⇒ Vertex 간의 관계
-
방향성
- 무방향 그래프
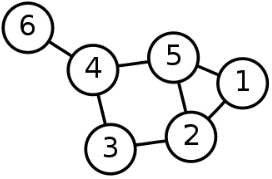
- 방향 그래프
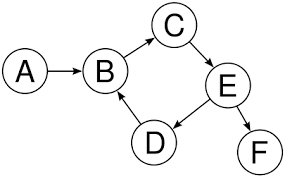
- 무방향 그래프
-
Arc
- 간선(Edge)과 같은 의미로 사용되며 방향성이 있는 그래프에서의 간선(Edge)을 의미한다.
- 간선(Edge)과 마잔가지로 두 vertex를 연결한다는 점이 같지만 간선(Edge)의 경우 A-B와 B-A를 동일하게 표시하지만, Arc의 경우 A → B, B → A는 서로 다르게 취급한다.
-
가중치(weight)
- a.k.a 비용(Cost). 두 노드를 연결하는 경로의 길이는 경로에 포함된 가중치의 합으로 정의. 최단 경로는 경로의 길이가 가장 짧은 경로로 정의.
- 가중치가 있는 그래프
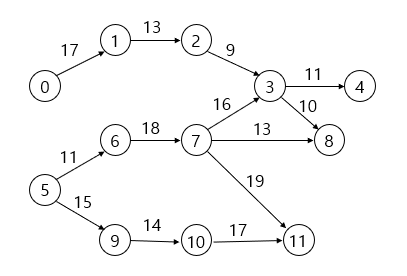
-
분지수(degree)
- in-deg(u)(in-dgree): 노드 u로 들어오는 방향 에지의 개수
- out-deg(u)(out-dgree): 노드 u에서 나가는 방향 에지의 개수
- deg(u) (degree of vertex) : 노드 u에 연결된 무방향 에지의 개수
- deg(G) (degree of graph) : 무방향 그래프 G의 최대 노드 분지수
-
사이클(cycle) ⇒ 한 노드에서 해당 노드로 다시 돌아오는 원형 구조
-
트리 ⇒ 사이클이 없는 연결 그래프
-
신장 그래프 → 부 그래프 중 모든 그래프의 노드가 등장하는 그래프
그래프의 표현 방식
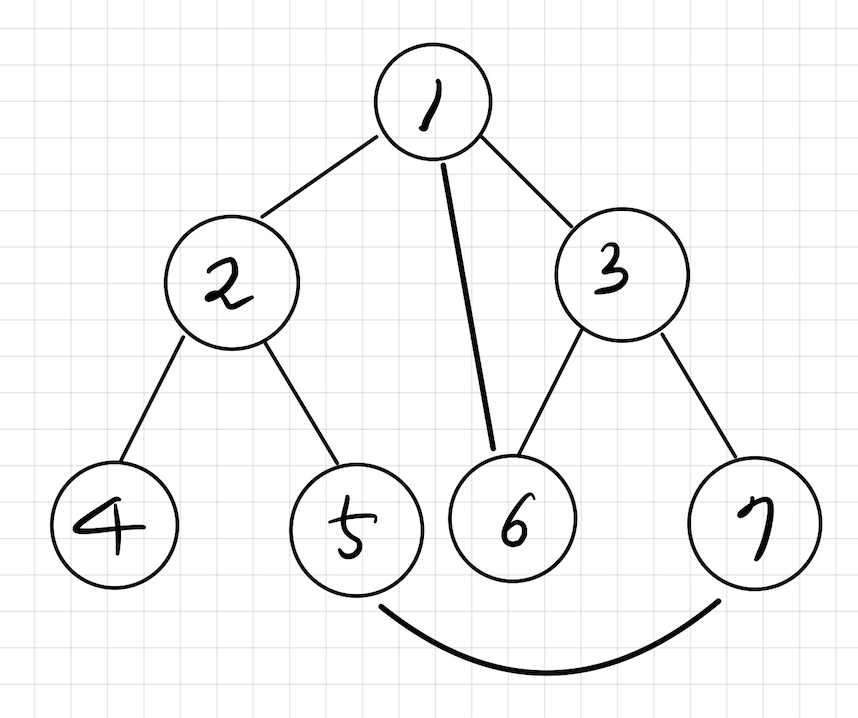
- 인접 리스트 (Adjacency Matrix)

- 인접 행렬 (Adjacency List)

깊이 우선 탐색(Depth First Search, DFS)
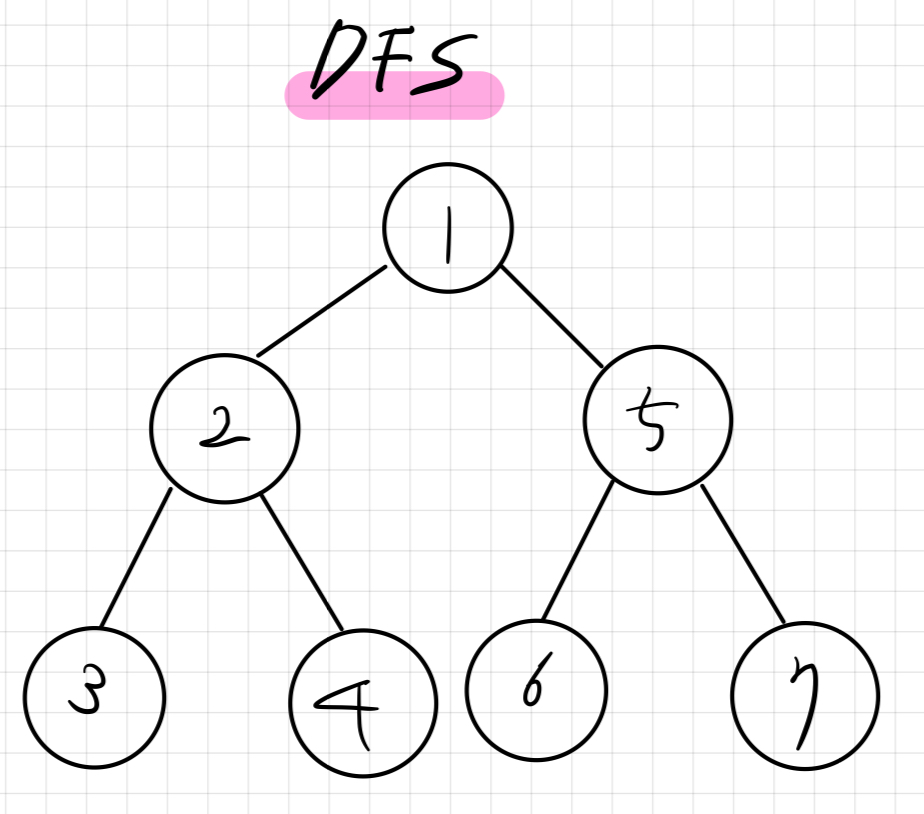
루트 노드에서 시작해서 다음 분기로 가기 전에 해당 분기를 완벽하게 탐색하는 것을 말한다.
- 모든 노드를 방문하는 경우 사용
- 깊이 우선 탐색이 너비 우선 탐색보다 간단.
- stack 또는 재귀함수를 통해 구현
def recursive_dfs(v, discovered = []):
discovered.append(v)
for w in adj_list[v]:
if not w in discovered:
discovered = recursive_dfs(w, discovered)
return discovered
def loop_dfs(start):
discovered = [ ]
stack = [start]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in adj_list[v][::-1]:
stack.append(w)
return discovered
너비 우선 탐색(Breadth-First Search, BFS)
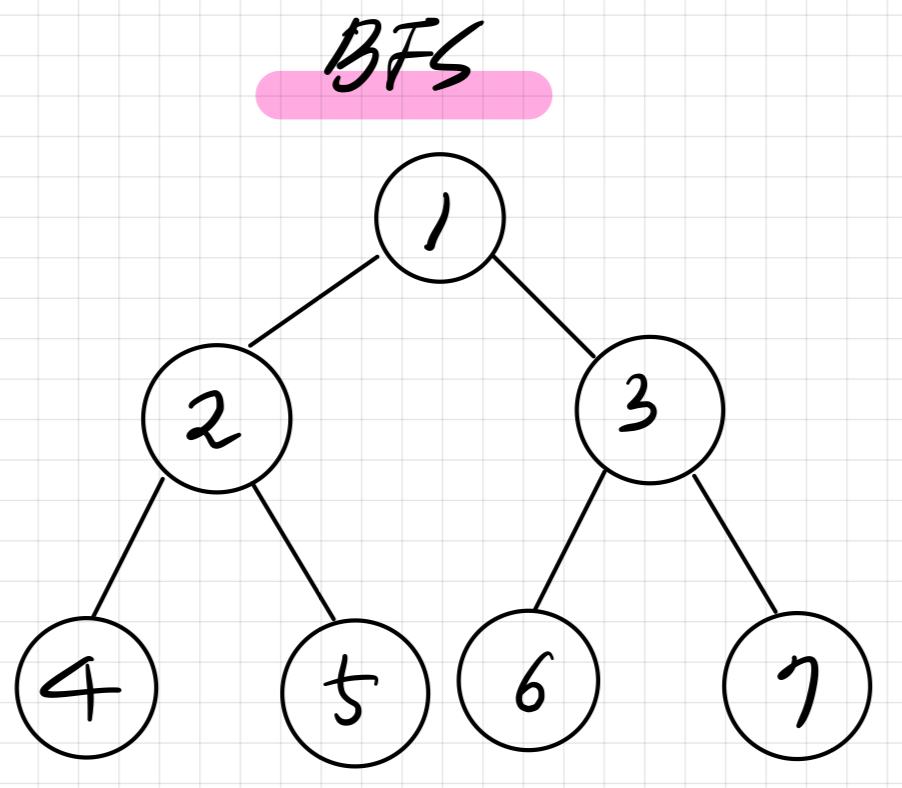
루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법.
- 노드 사이 최단 거리를 찾고 싶을 때 사용
- 큐를 통해 구현
def bfs(start):
discovered = [ start ]
queue = [ start ]
while queue:
v = queue.pop(0)
for w in adj_list[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discoveredDFS / BFS 구현해보기 🤔
[백준][Python] 1260번 DFS와 BFS(DFS/BFS 기본 구현 자세히)
백 트래킹 (Back Tracking)
한정 조건에 한해서 모든 경우의 수를 시도하는 문제 해결 방법. ‘한정 조건’으로 인해 많은 경우의 수가 배제되기 때문에 다중 for문 보다 빠른 속도로 문제를 해결할 수 있다.
백 트래킹의 경우 ‘한정된 조건 내에서 모든 경우를 탐색하는 방법’이므로 완전 탐색 기법인 BFS(Breadth First Search)와 DFS(Depth First Search)로 구현한다.
구현에 있어서는 특정 노드를 방문해서 한정 조건을 검사하고 조건에 부합하지 않은 경우 다시 이전 노드로 돌아와야하기 때문에 BFS보다 DFS로 구현을 하는 경우가 더 편하다.
트리 순회
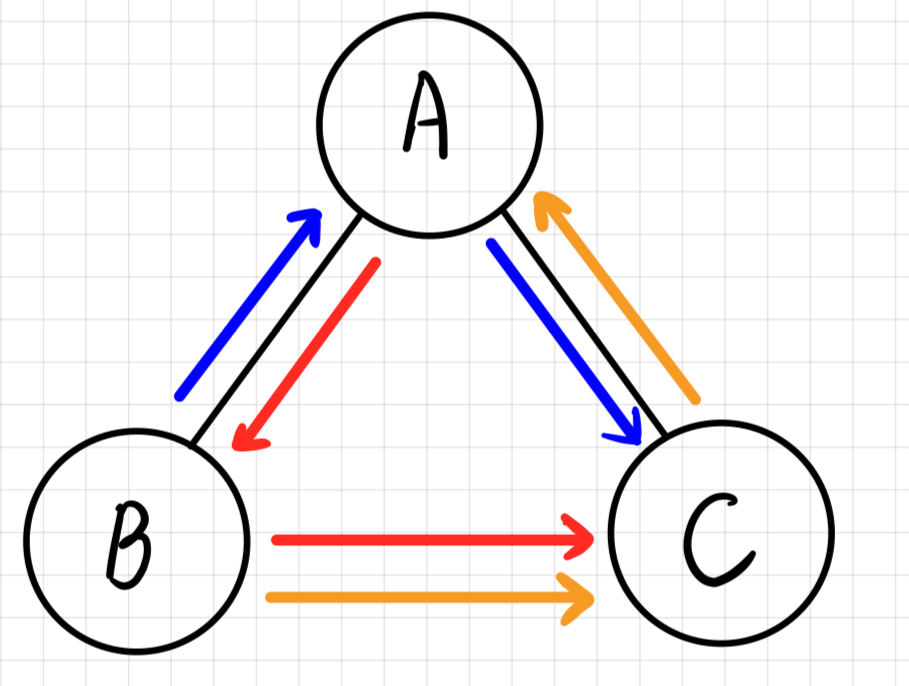
전위 순회: A → B → C
중위 순회: B → A → C
후위 순회: B → C → A
Reference
graph algorithm(요즘 IT) : https://yozm.wishket.com/magazine/detail/2411/
DFS/BFS (tistory blog) : https://devuna.tistory.com/32

