TIL - 2024/03/30
트라이 (Trie)
트라이는 문자열을 저장하교 효율적으로 탐색하기 위한 트리형태의 자료구조를 말한다.
실생활에서 ‘자동완성 기능’, ‘사전 검색’ 등에서 텍스트를 빠르게 검색할 때 주로 사용되고 있다.
래딕스 트리(Redix Tree), 접두사 트리(Prefix Tree), 탐색 트리(Retrieval Tree)라고도 불린다.
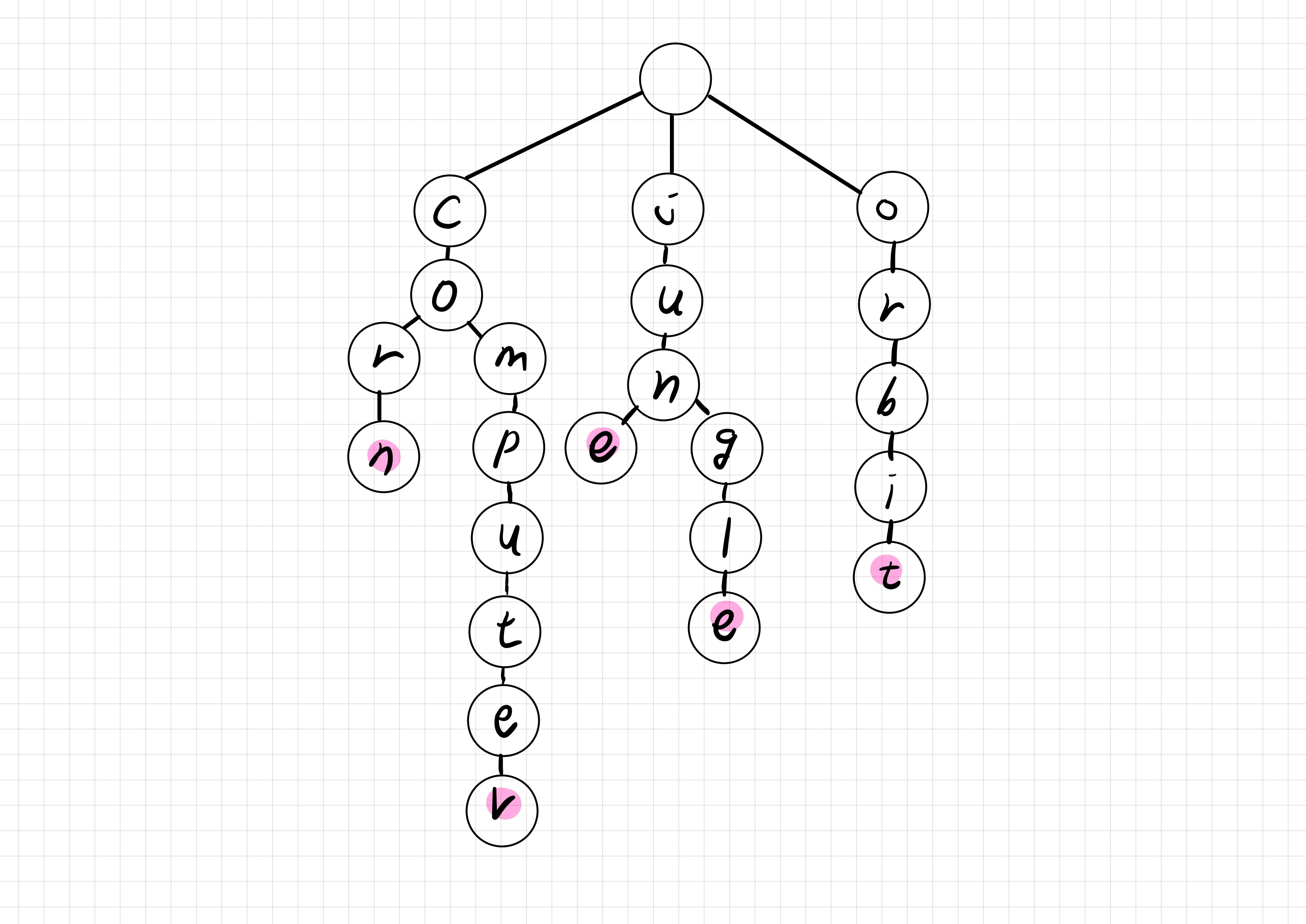
동작 과정
- 한 문자에 대해서 다음 문자들을 자식 노드로 넣는다.
- 문자열과 동일한 문자열이 나올때 까지 자식노드를 따라간다.
장점
- 문자열에 대해서 빠른 검색이 가능하다.
- 문자열의 길이만큼만 노드를 따라가면 되기 때문에 검색 과정은
O(L)의 시간 복잡도를 가진다. - 트라이에 단어를 삽입하는 경우 모든 문자열을 특정 노드 끝에 넣기 때문에
O(M * L)의 시간 복잡도를 가진다.
단점
- 많은 메모리가 소모된다.
- 영어 단어만이라고 하더라도 매 자리마다 모든 알파벳을 저장해야할 수 있기 때문에 메모리의 양이 매우 많이 소모된다.
Example
class Node(object):
def __init__ (self, key, has_end = False):
self.key = key
self.data = data
self.children = dict()
class Trie(object):
def __init__ (self):
self.head = Node(None)
def insert(self, string):
curr_node = self.head
for char in string:
if curr_node.children.get(char) is None:
curr_node.chiuldren[chr] = Node()
curr_node = curr_node.children[char]
curr_node.is_terminal = True
def search(self, string):
curr_node = self.head
for char in string:
if curr_node.children.get(char) is None:
return False
curr_node = curr_node.children[char]
return True관련 문제 : https://www.acmicpc.net/problem/5052
Python get value from dict
a_dict = {
'name': 'Paul',
'age': 12,
}
>>> a_dict['height'] # KeyError...! 😅
>>> a_dict.get('height') # None 😁
>>> a_dict.get('hegiht', 180) # 180 🤩
# 두번째 인자 값을 통해 default 값을 설정해서
# 해당 키의 값이 없는 경우에 default 값을 사용하게끔 할 수 있다.다익스트라 알고리즘(Dijstra Algorithm)
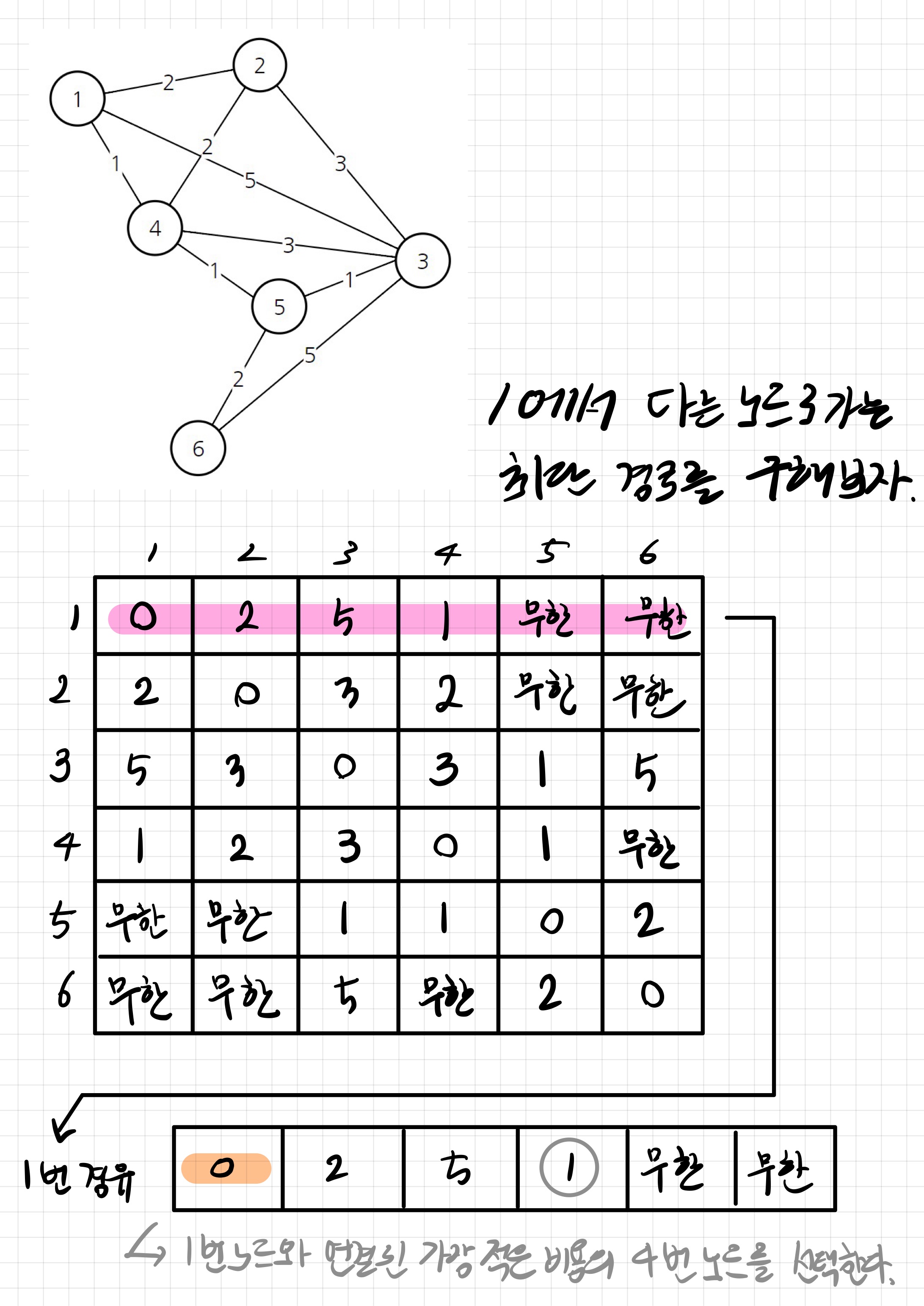
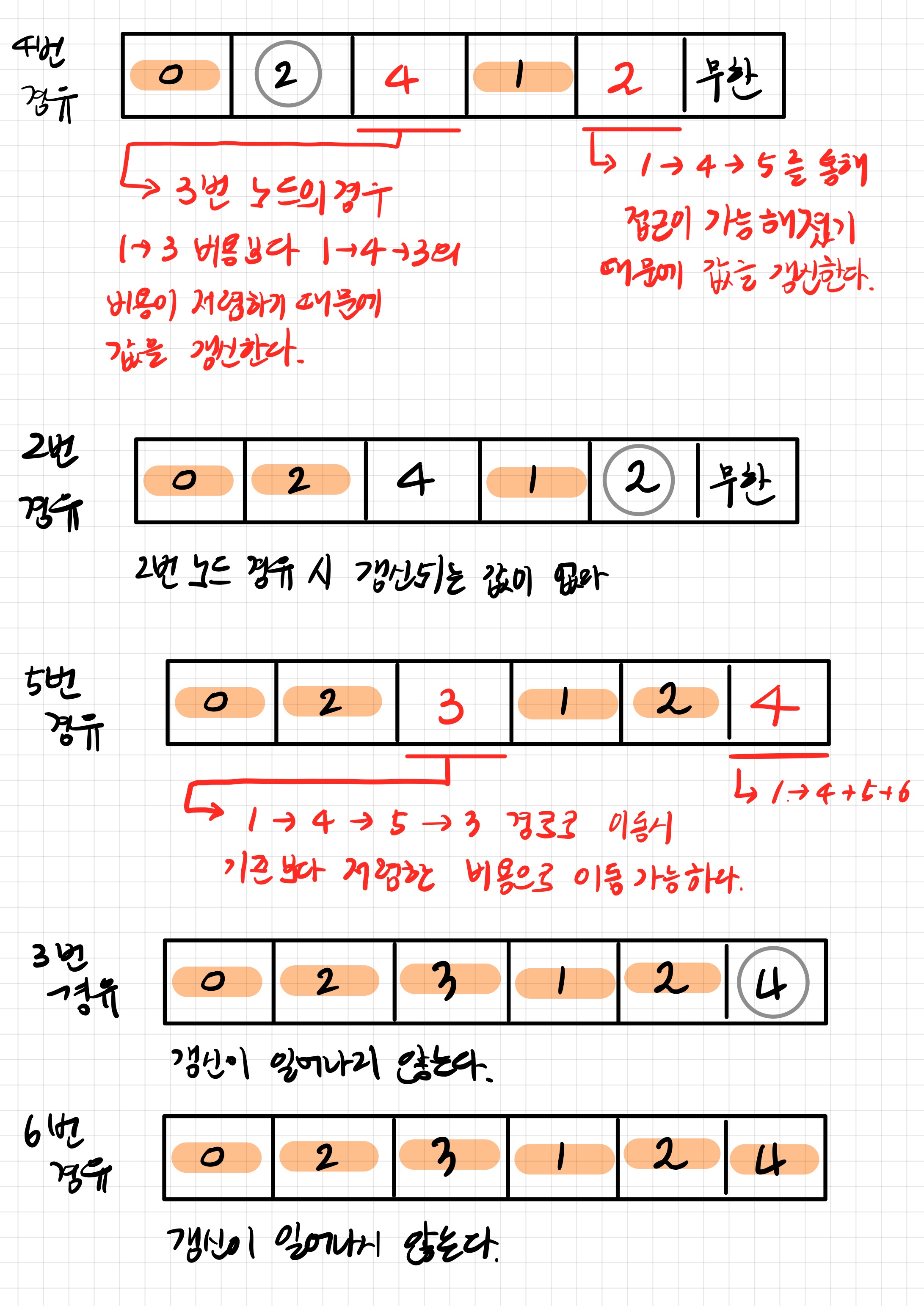
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 최단 경로 탐색 알고리즘이다.
하나의 정점에 대해서 다른 정점으로 가능 최단 경로를 알 수 있다. 이때 음의 가중치를 가지는 간선에 대해서는 고려하지 않기 때문에 현실세계에 적용하기 적합한 알고리즘으로 볼 수 있다.
참고: https://blog.naver.com/ndb796/221234424646
플로이드-워셜 알고리즘(Floyd-Warshell Algorithm)
가중치 그래프에서 최단 경로를 찾는 알고리즘. 다익스트라의 경우 한 정점에서 다른 모든 정점에 대한 최단 경로를 구하는 알고리즘이다. 하지만 플로이드-워셜 알고리즘은 모든 정점에 대한 모든 정점으로의 최단 거리를 구하는 알고리즘이다.
플로이드 워셜 알고리즘은 거쳐가는 정점을 기준으로 최단거리 알고리즘을 수정한다는 특징이 있다.

