
이진 트리 (Binary Tree)
자식 노드를 2개 이하로 가지는 트리.
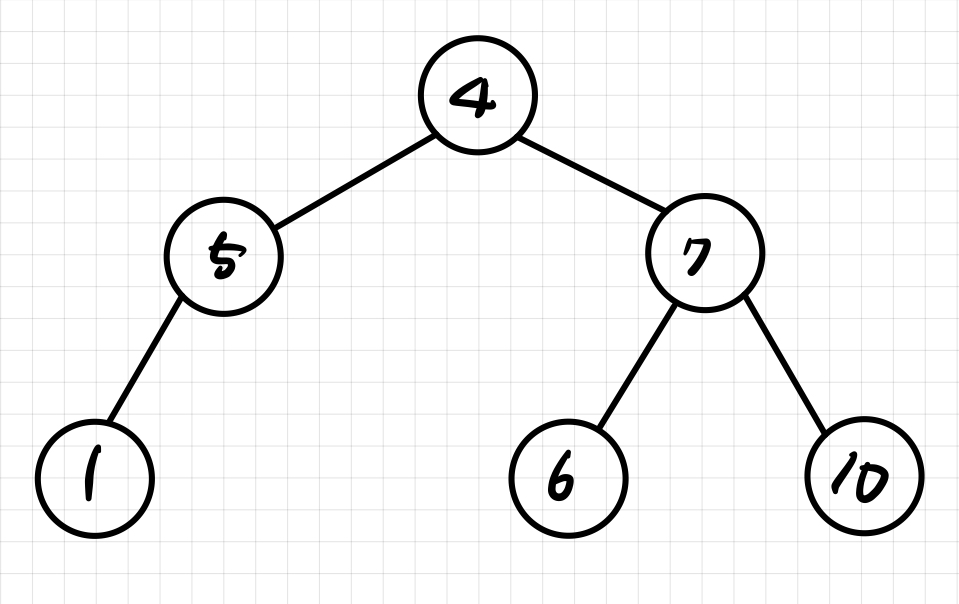
완전 이진 트리
마지막 레벨의 노드, 즉 leaf 노드를 제외하고 모든 레벨이 완전히 채워져 있어야하며, 마지막 레벨의 모든 노드는 왼쪽부터 채워져있어야 한다. 마지막 레벨 h에서 루트 노드까지 총 2^h - 1개의 노드를 가질 수 있다.
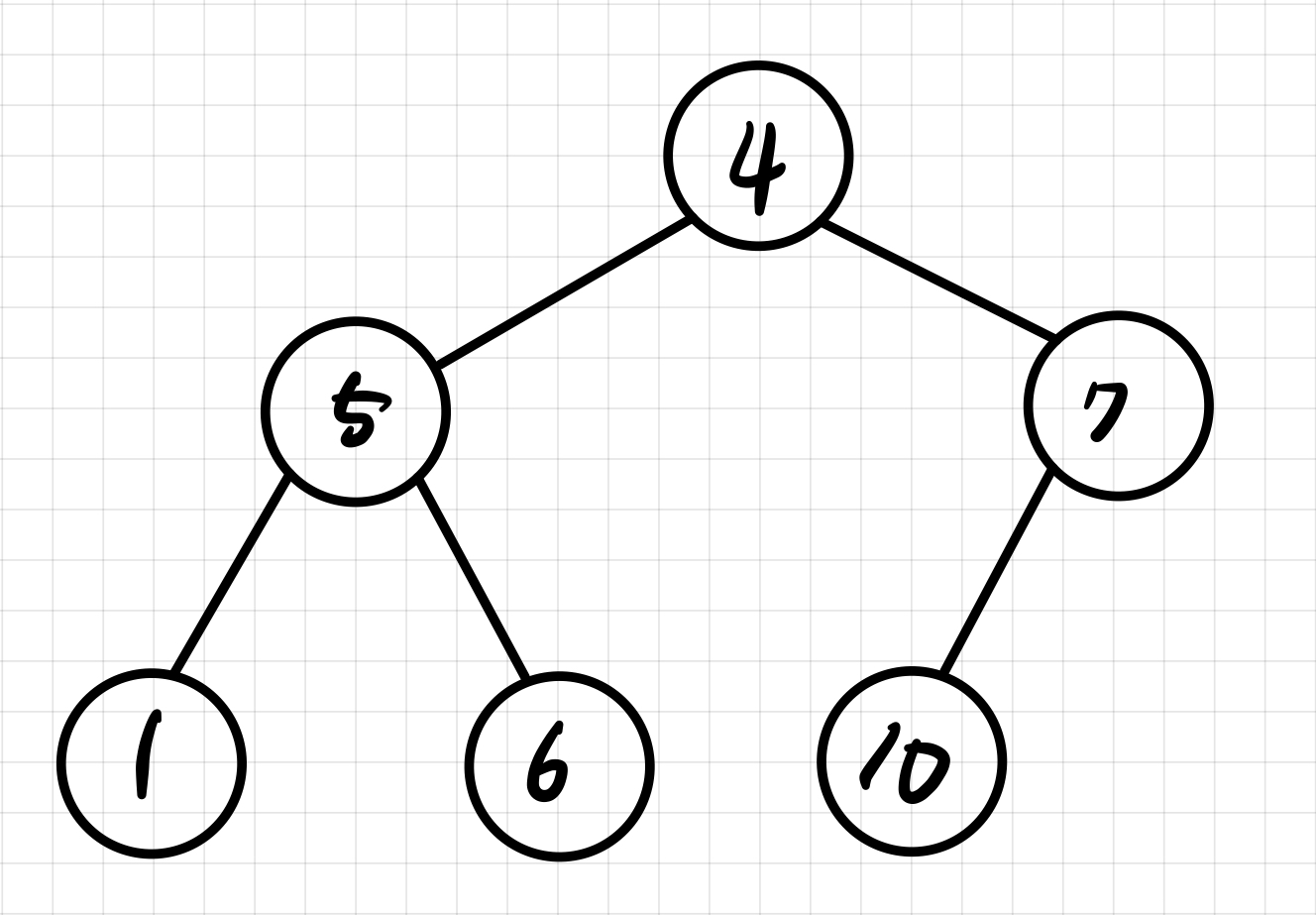
이진 탐색 트리
효율적인 탐색( O(log N) )을 위한 이진 트리로 노드를 기준으로 왼쪽에는 노드의 키값 보다 작은 값이, 오른쪽에는 노드의 키 값보다 큰 값이 들어간다.
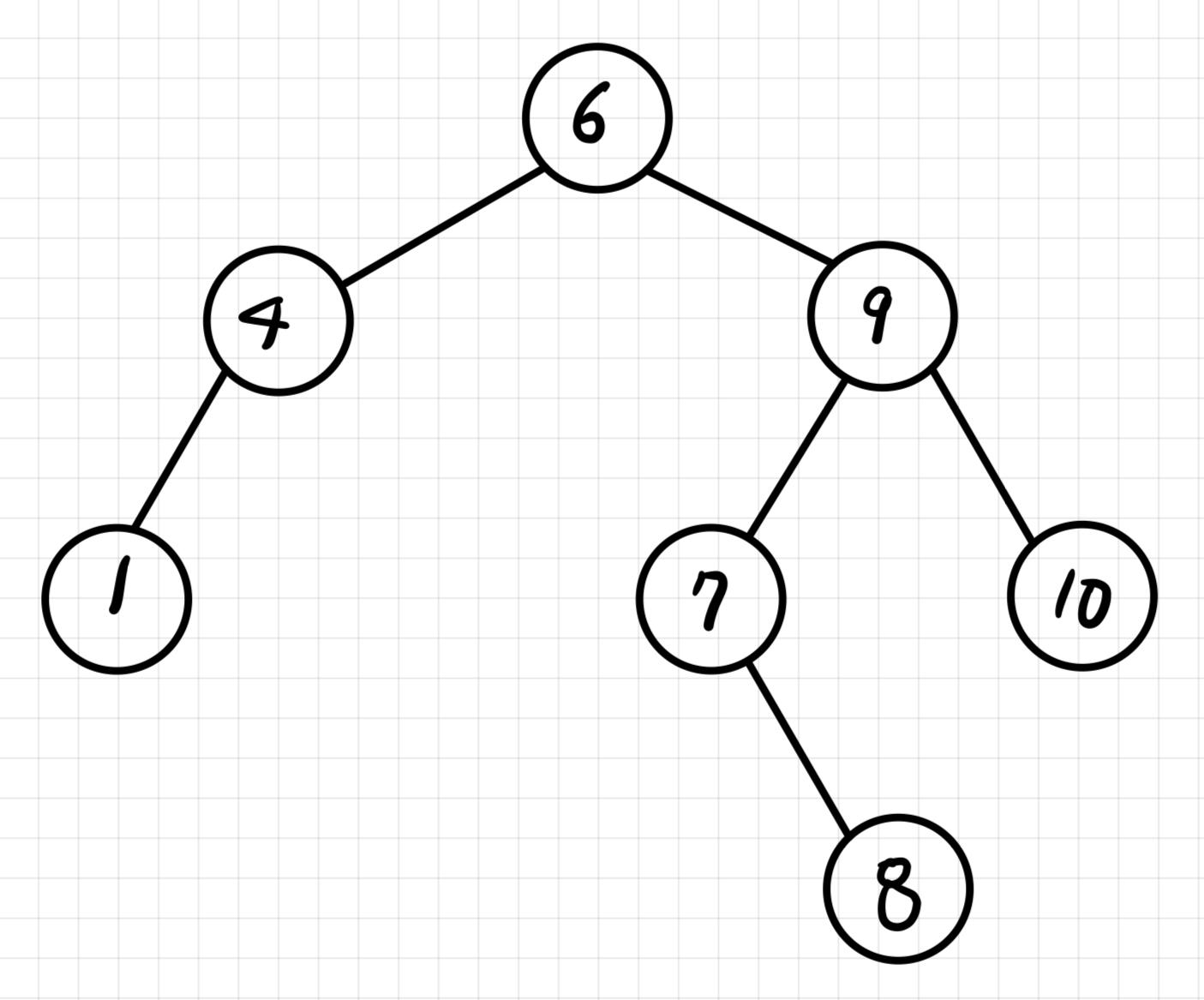 하지만 이진 탐색 트리는 루트 노드의 값에 따라 루트 노드를 기준으로 한쪽에 기울어진 형태의 트리를 가지게 된다.
하지만 이진 탐색 트리는 루트 노드의 값에 따라 루트 노드를 기준으로 한쪽에 기울어진 형태의 트리를 가지게 된다.
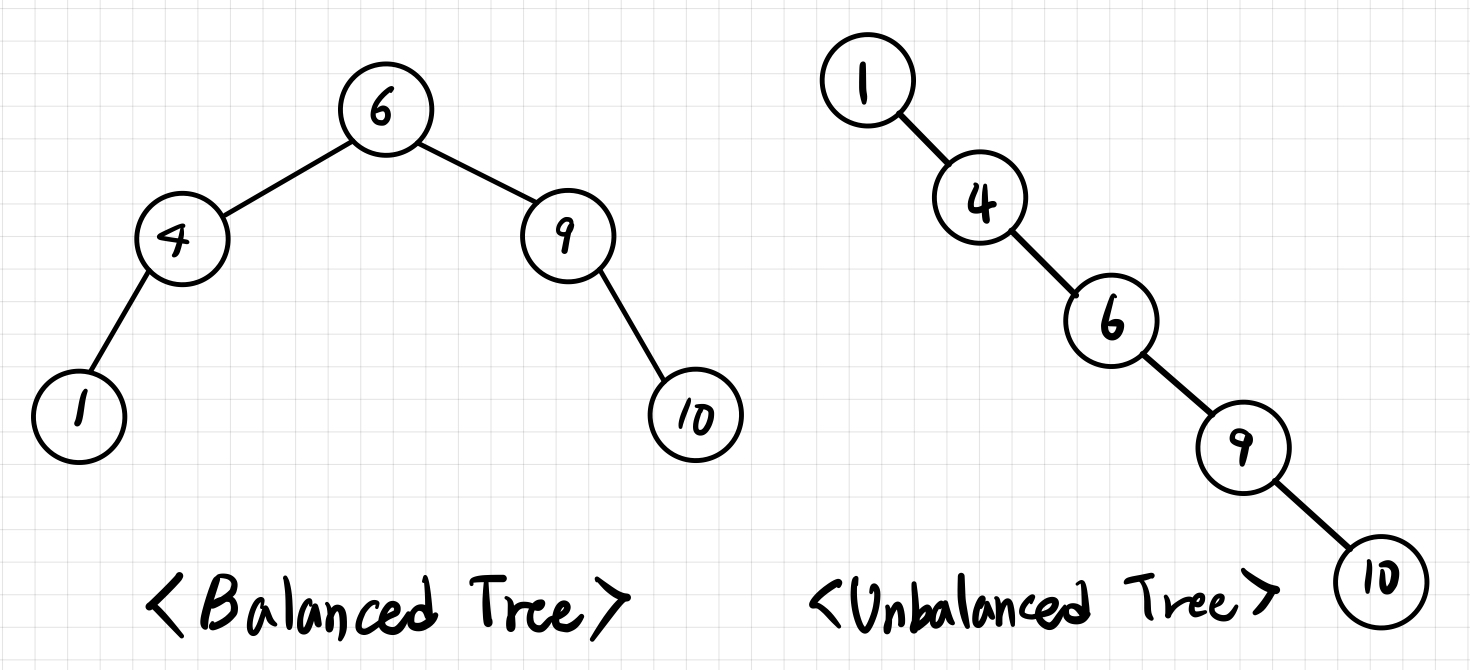 이러한 불균형에 의해서 이진 트리의 장점인 탐색 속도와 효율에 영향을 줄 수 있다.
이러한 불균형에 의해서 이진 트리의 장점인 탐색 속도와 효율에 영향을 줄 수 있다.
위 그림처럼 특정 한 방향으로만 이진 트리가 생성되는 경우 O(logN)보다 O(N)의 시간복잡도로 비효율적인 탐색 동작하게 된다.
-
추가적인 단점
- 메모리 : 이진 트리에서 각 노드는 좌/우 노드를 저장하는 메모리가 추가로 필요한 자료구조이다. 데이터가 많아지고, 트리가 깊어질수록 메모리 사용량이 늘어난다.
- 삽입 및 삭제 연산의 비효율성 : 삽입과 삭제를 하는 과정에서 트리의 불균형을 재조정(rebalancing)하는 과정이 필요할 수 있다. 이런 과정 때문에 성능이 저하 될 수 있다.
- 메모리 : 이진 트리에서 각 노드는 좌/우 노드를 저장하는 메모리가 추가로 필요한 자료구조이다. 데이터가 많아지고, 트리가 깊어질수록 메모리 사용량이 늘어난다.
균형 이진 트리 ( Balanced Binary Tree )
이진 트리의 단점인 불균형을 보완하기 위한 트리. 리프 노드들의 깊이 차이가 크지 않은 트리를 말한다. 균형을 우지함으로서 이진 트리의 탐색, 삽입, 삭제를 균형적으로 수행할 수 있게 해준다.
대표적으로 AVL Tree, Red-Balck Tree가 있다.
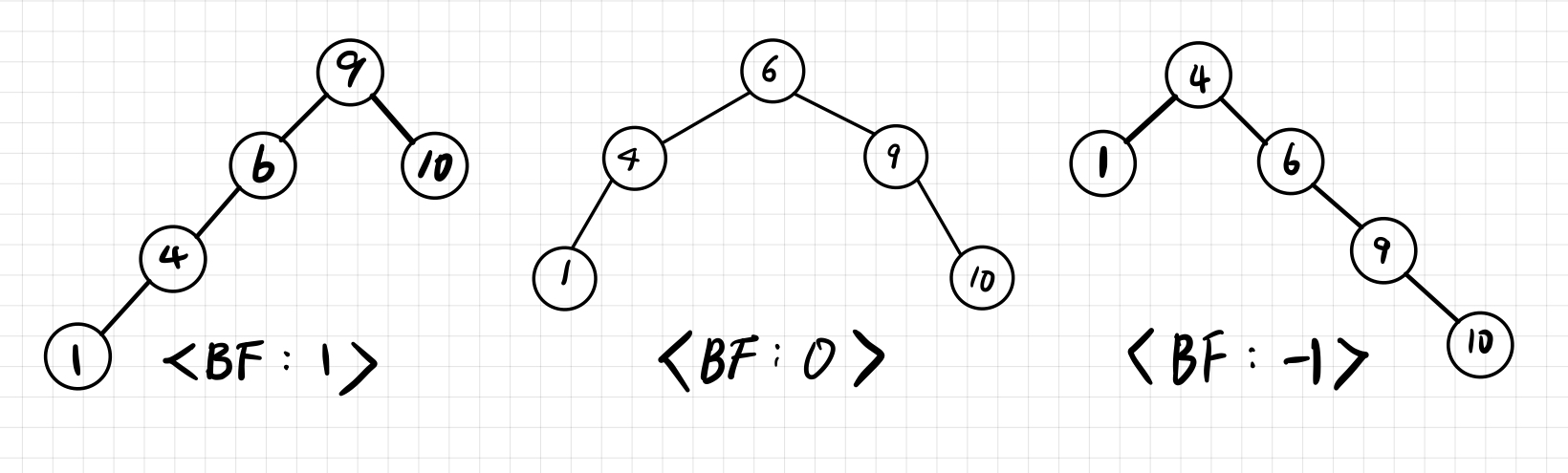
트리의 균형을 파악하는 요인을 BF(Balanced Factor)라고하는데, 왼쪽 노드의 높이에서 오른쪽 노드의 높이를 뺀 값으로 계산할 수있다.
따라서 균형 트리는 BF를 -1, 0, 1만 가지는 트리라고 할 수 있다.
 균형 이진 트리의 특징
균형 이진 트리의 특징
- 균형 : 일반적으로 깊이 차이를 1로 유지되어야 하며, 트리의 높이를 최소화하여 연산의 시간복잡도를 O(logN)을 유지한다.
- 균형 조정 : 이진 트리의 삭제, 삽입 연산시 자동으로 균형을 d유지하기 위한 연산이 수행된다.
회전
트리의 균형을 유지하기 위해 회전연산을 수행한다.
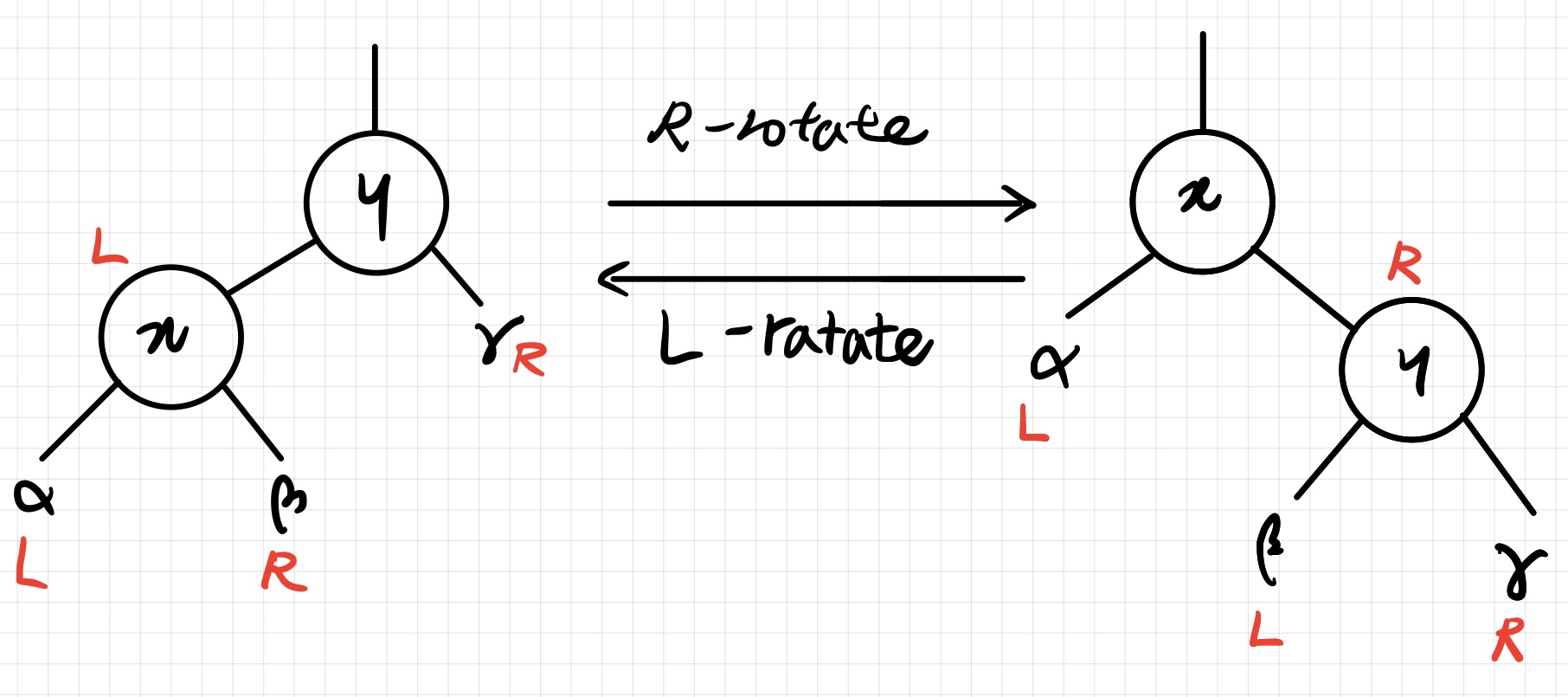
R-Rotate pseudo-code
RIGHT_ROTATE( T, y ):
x = y.left // Set x with y node's left node
y.left = x.right // Connect y node's left with x node's right child
if x.right != T.nil:
x.right.p = y
x.p = y.p // Connect x with parent of y node
if x.p == T.nil:
T.root = x
elseif y == y.p.left:
y.p.left = x
else
y.p.right = x
x.right = y
y.p = xL-Rotate pseudo-code
LEFT_ROTATE( T, x ):
y = x.right //Set y with x's right node
x.right = y.left
if y.left != T.nil: //Connect x node's right with y node's left child
y.left.p = x
y.p = x.p
if x.p == T.nil:
T.root = y
elseif x == x.p.left:
x.p.left = y //Connect y with parent of x node
else
x.p.right = y
y.left = x
x.p = yRotate Case
Left - Left Case
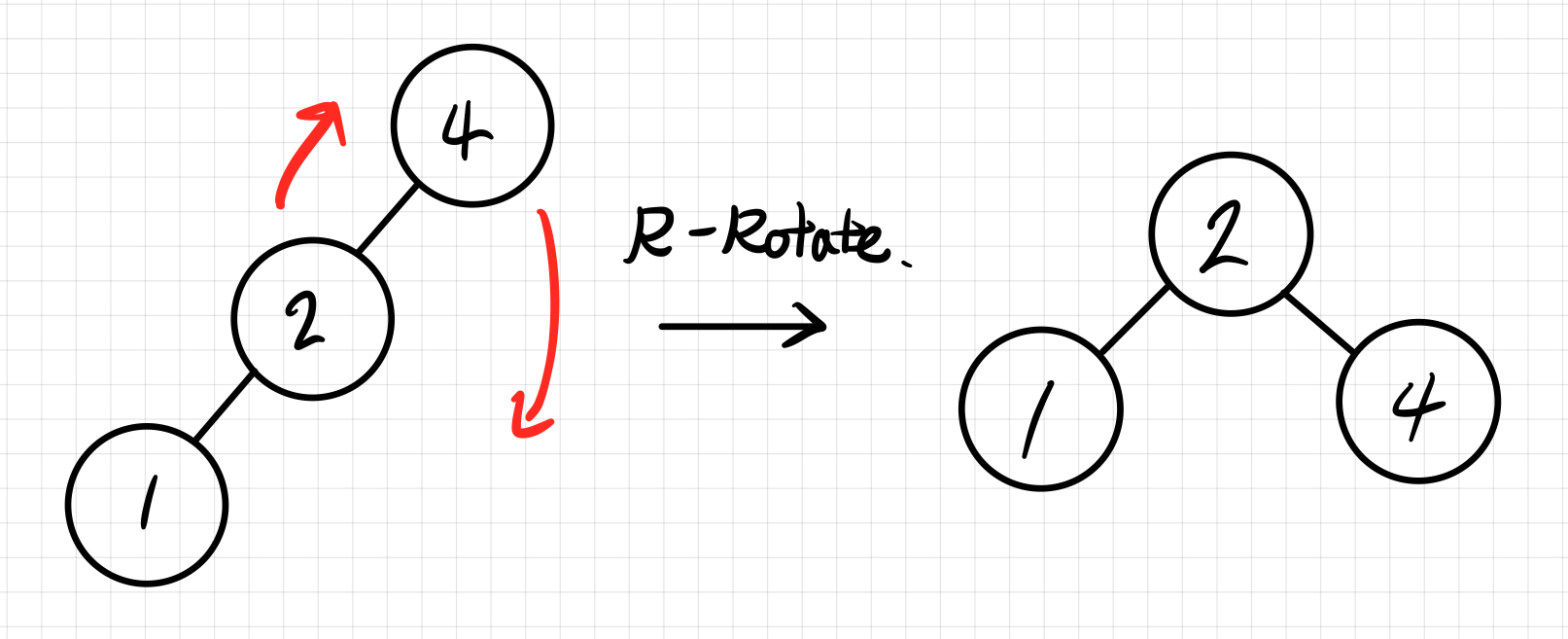
Right - Right Case
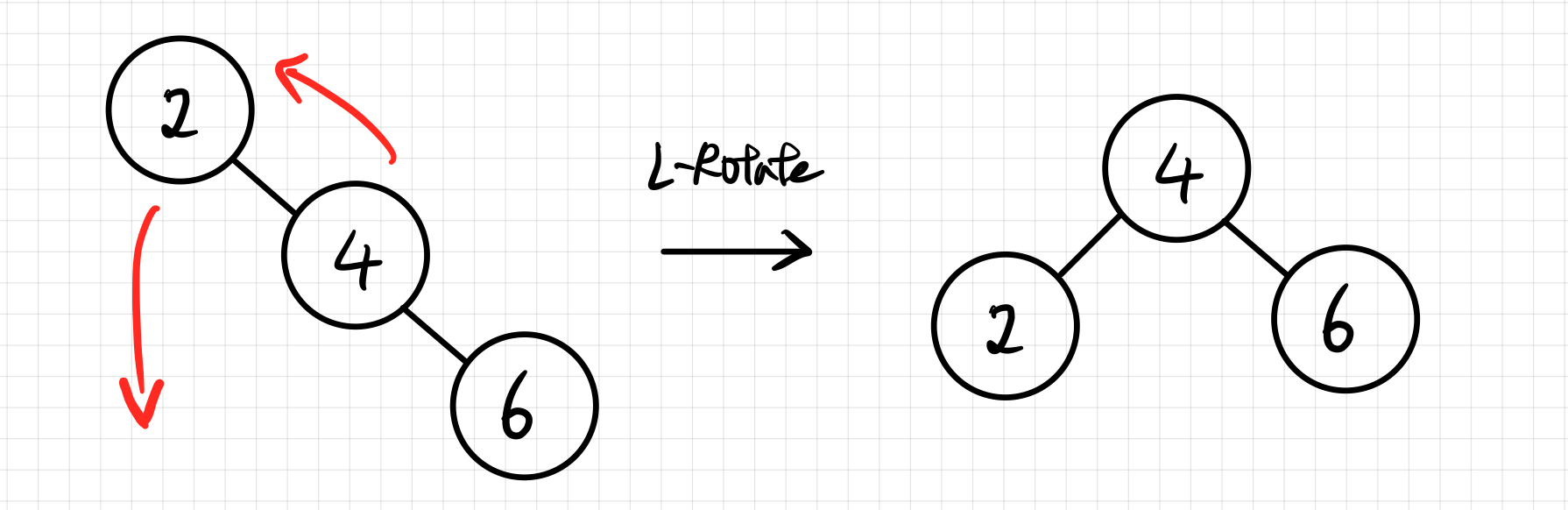
Left - Right Case
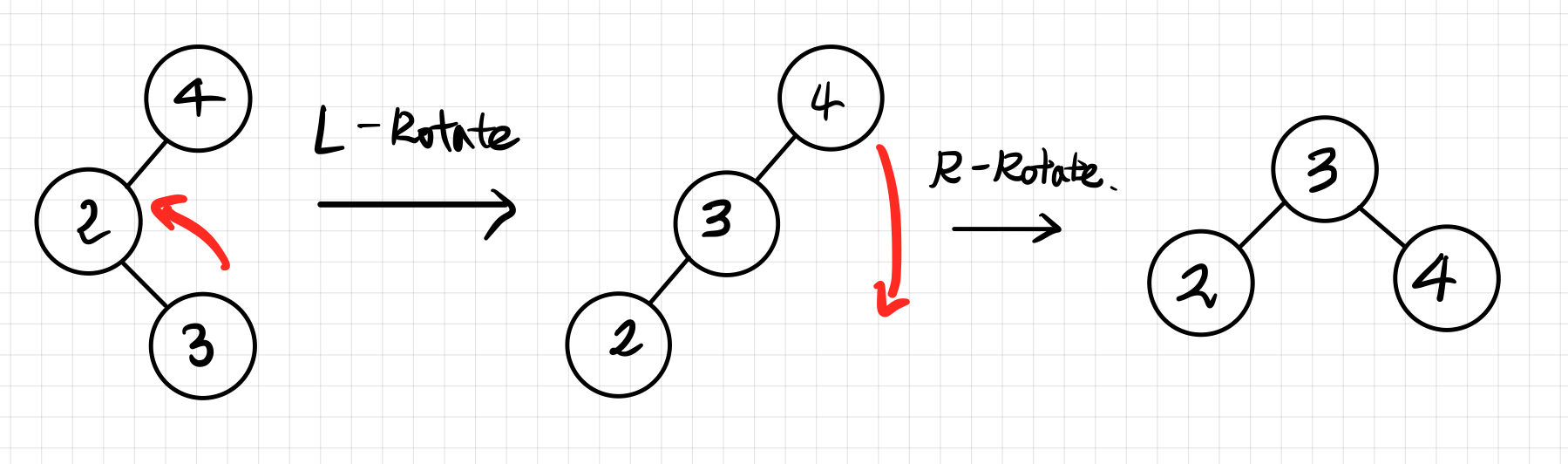
Right - Left Case
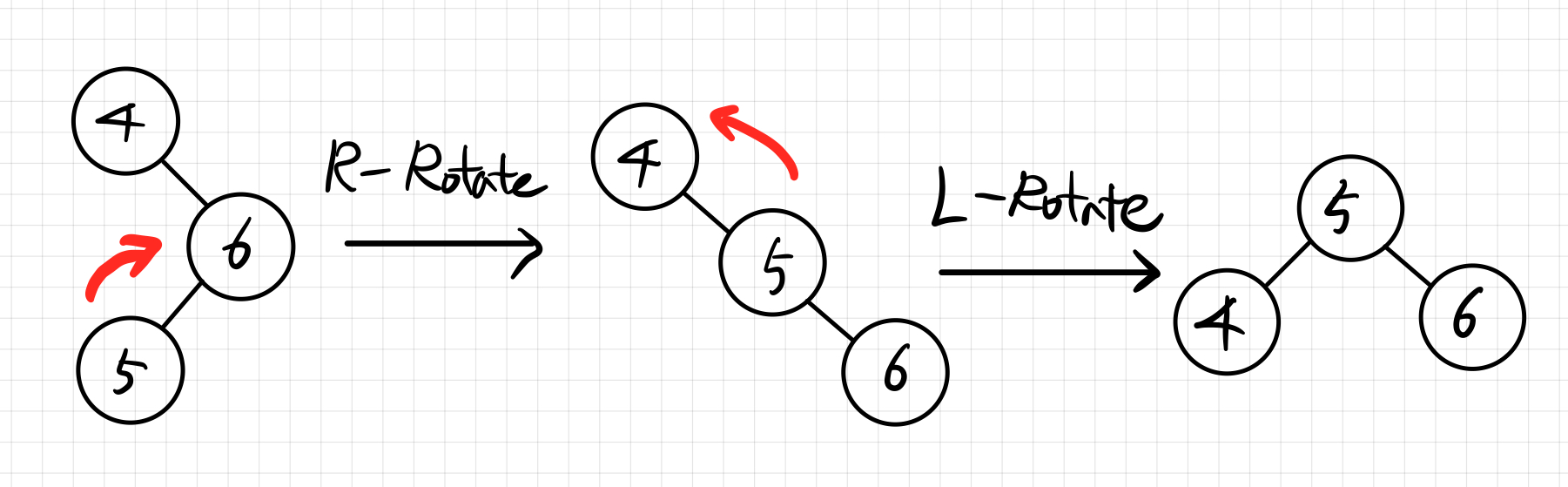
Red-Black Tree
개요 ( 영문 위키 번역 )
CS에서 red-black 트리는 빠른 저장과 정렬된 정보를 회수하고, 일정 시간내 동작을 마무리하는 것을 보장하는데 특화되어있는 이진 탐색 트리 구조이다. 다른 자가 균형 이진 탐색 트리와 달리, red-black tree의 노드들은 여분의 bit 공간을 가지고 있다.
이 공간에는 ‘Red’, ‘Black’으로 구분 되는 ‘색깔’ 정보를 저장한다. 이 색깔 정보는 트리가 항상 거의 균형 잡혀있음을 보장하기 위한 재구조화(re-organizing)를 할때 사용된다.
트리가 수정될 때, 새로운 트리는 최악의 케이스가 될 수도 있는 균형잡히지 않은 트리의 불균형 상태를 막기 위해서 색깔 속성을 수정하는 rearrange와 repainting 과정을 거친다. 이러한 특성들은 rearrange와 repainting 과정이 효율적으로 수행될 수 있도록 설계되었다.
이런 리밸런싱 과정이 완벽하진 않지만, n개의 요소가 트리에 있을때 시간 복잡도가 항상 O(logN)이 되는 것을 보장한다. 트리의 rearranging과 recoloring이 동반된 삽입과 삭제도 마찬가지로 O(logN)의 시간복잡도로 수행된다.
각 노드의 색을 추적하기 위해서 단 두개의 색만 사용하기 때문에 노드별로 1비트의 공간만 필요하다. 트리는 red-black tree애 대한 다른 고유 정보를 포함하고 있지 않기 때문에, 일반적인 이진 탐색 트리와 메모리 사용량이 거의 동일하다. 어떤 경우에는 추가 비트에 대한 메모리 비용없이 저장할 수도 있다.
용어
Red-Black Tree는 이진 탐색 트리의 특별한 종류 중 하나로, 텍스트 조각이나 숫자와 같은 비교 가능한 데이터의 조각을 정리하기 위해 사용하는 트리이다. key나 데이터를 옮기는 노드들은 ‘internal node’라고 불리기도 하고 ’non-NIL node’라고도 한다.
red-black tree의 리프노드는 key나 데이터를 가지지 않는다. 이 리프 노드들은 컴퓨터 메모리 내에서 각각 명시적으로 구분될 필요가 없다. 그래서 이진 트리 구조에서 사용하는 NULL 포인터를 사용해서 해당 노드에서는 자식 노드가 존재하지 않는다고 표현할 수 있다. 하지만 리프 노드의 자식들은 값이 없는 NULL 포인터로 표현하는 대신 NIL이라는 노드로 표현한다. NIL노드는 실제 값을 가지고 있는 노드는 아니지만 이후 삽입 과정에서 삽입의 위치를 표현하는 역할을 한다.
아래 사진(출처: red-black Tree Wiki)처럼 모든 리프 노드에 NIL 노드를 부여할 수 있지만 결국 경로의 끝, 노드 삽입 위치로 같은 의미를 가지기 때문에 고유한 NIL노드에 연결하여 구현하기도 한다.
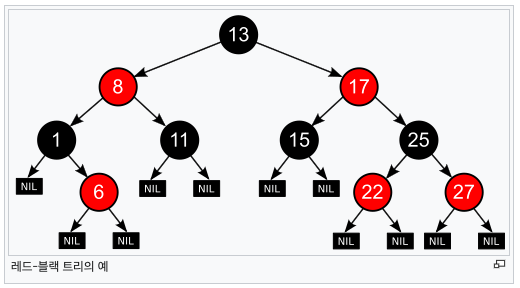
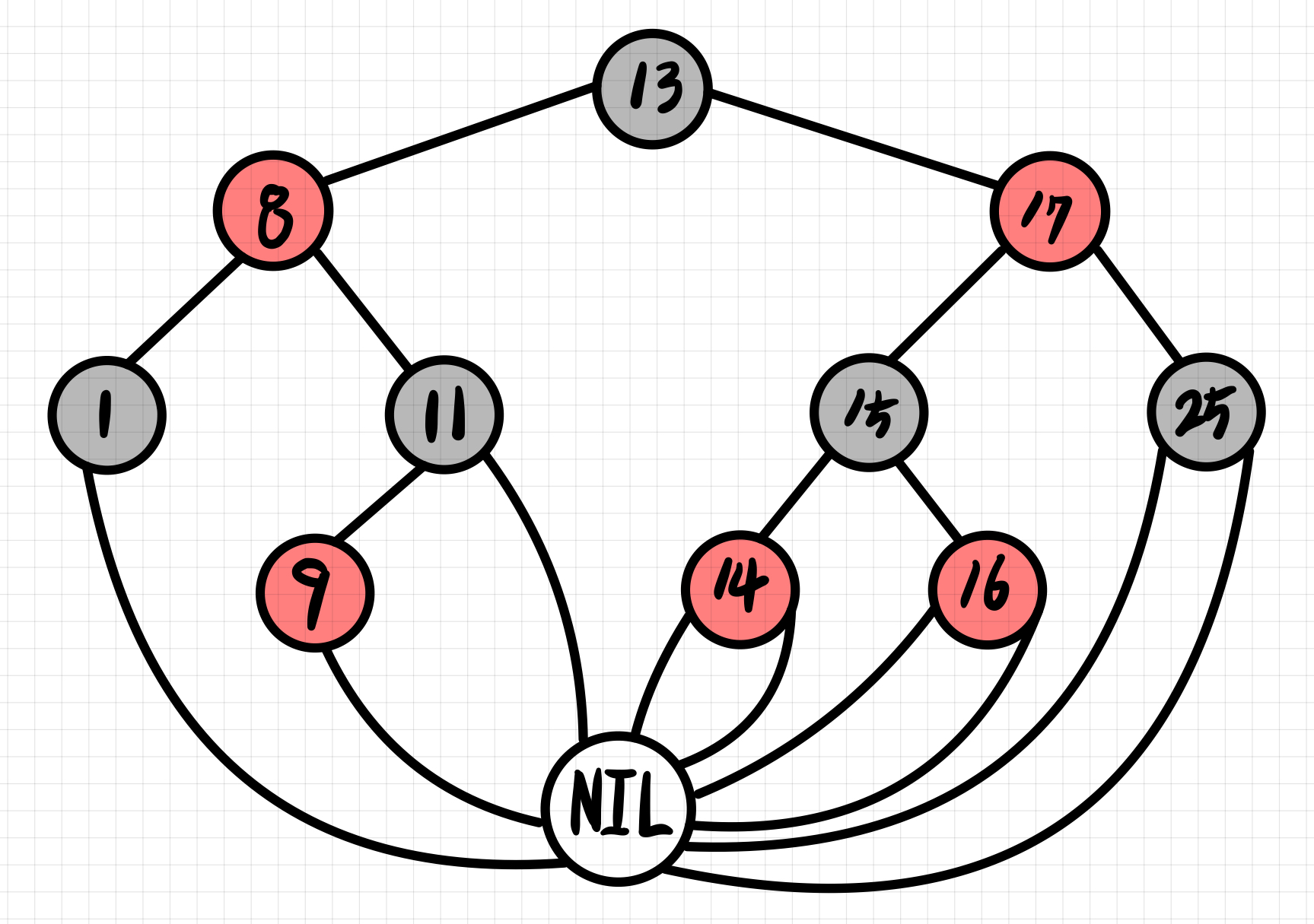
하나의 NIL 노드만 사용함으로서 각 노드마다 NIL 노드를 부여하는 것 보다 메모리를 절약할 수 있다.
트리의 높이
Black Depth는 루트노드에서 해당 노드까지 이동하면서 만난 Black 노드의 수를 의미한다. Red-Black Tree에서 Black Height는 루트 노드에서 리프 노드로 가는 어떠한 경로로 가더라도 항상 같은 값을 보인다.
특성
Red-Black 트리는 이진 탐색 트리의 특성에 더불어 아래의 규칙을 만족해야한다.
- 모든 노드는 Red 또는 Black이다.
- 모든 NIL 노드는 Black 노드이다. 모든 루트 노드는 Black이다.
- Red 노드는 Red 자식 노드를 가질 수 없다. (Red 노드가 연속되면 안됨)
- 주어진 노드에서 노드보다 아래에 있는 NIL 노드로 가는 경로에는 항상 같은 수의 Black 노드(Black Height)를 가진다. ( 개수에 본인은 제외. )
- 만약 N 노드가 하나의 자식을 가진다면, 반드시 Red 노드여야 한다. ( 해당 노드가 Black 노드면, 하위 경로에 있는 Black 노드의 개수에 영향을 주기 때문에 4번 규칙에 위배된다. )
삽입이나 수정 작업에서 1, 2번의 규칙은 잘 지켜지지만, Red Violation이라고 불리는 3번 규칙, Black Violation이라고 불리는 4번 규칙을 적용하기 위한 별도의 조작이 필요하다.
Red-Black Tree 삽입 ( O(log N ) )
과정
- 삽입 전 RB 트리 속성을 만족한 상태
- 삽입 방식은 일반적인 BST의 삽입 방식과 동일
- 삽입후 RB트리의 규칙 위반 여부 확인
- 위반했다면, 재조정
- RB 트리 규칙 위반 여부 재확인
ex)
insert(15)
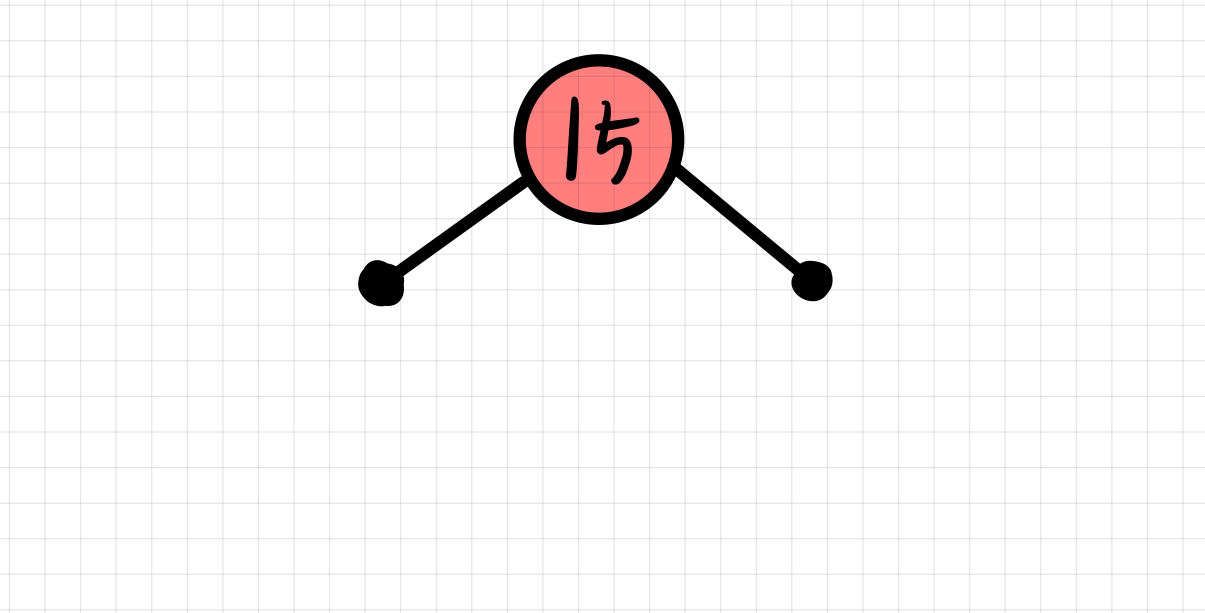
노드를 삽입한 후, 현재 2번 규칙을 만족하지 못하기 때문에 노드를 Black으로 바꾸어준다.
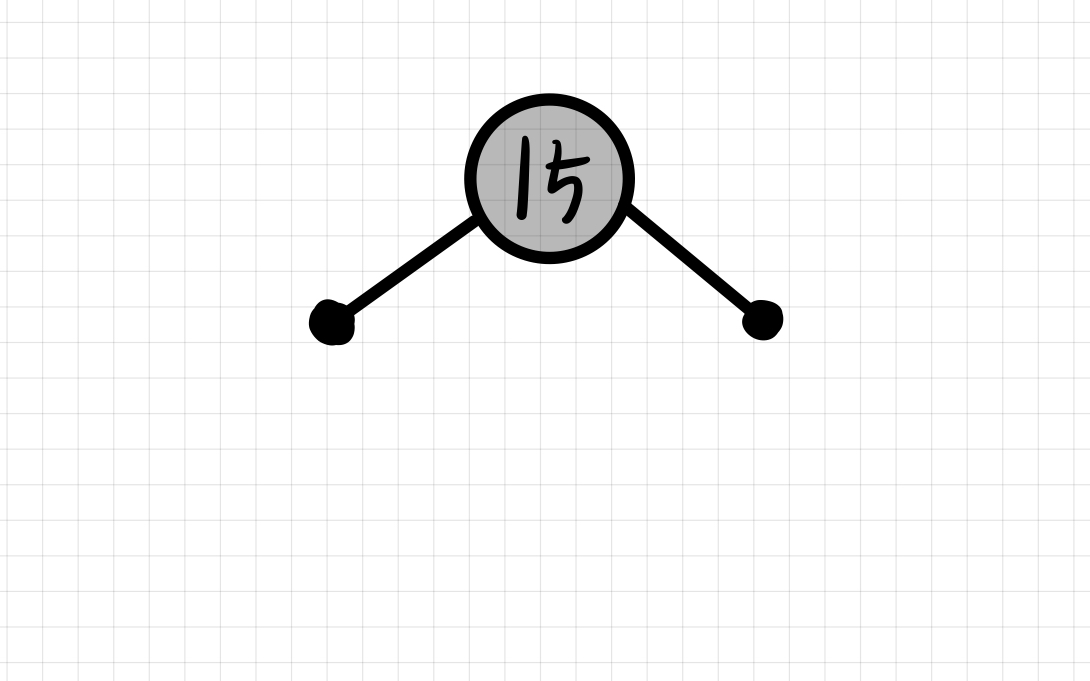
insert(10)
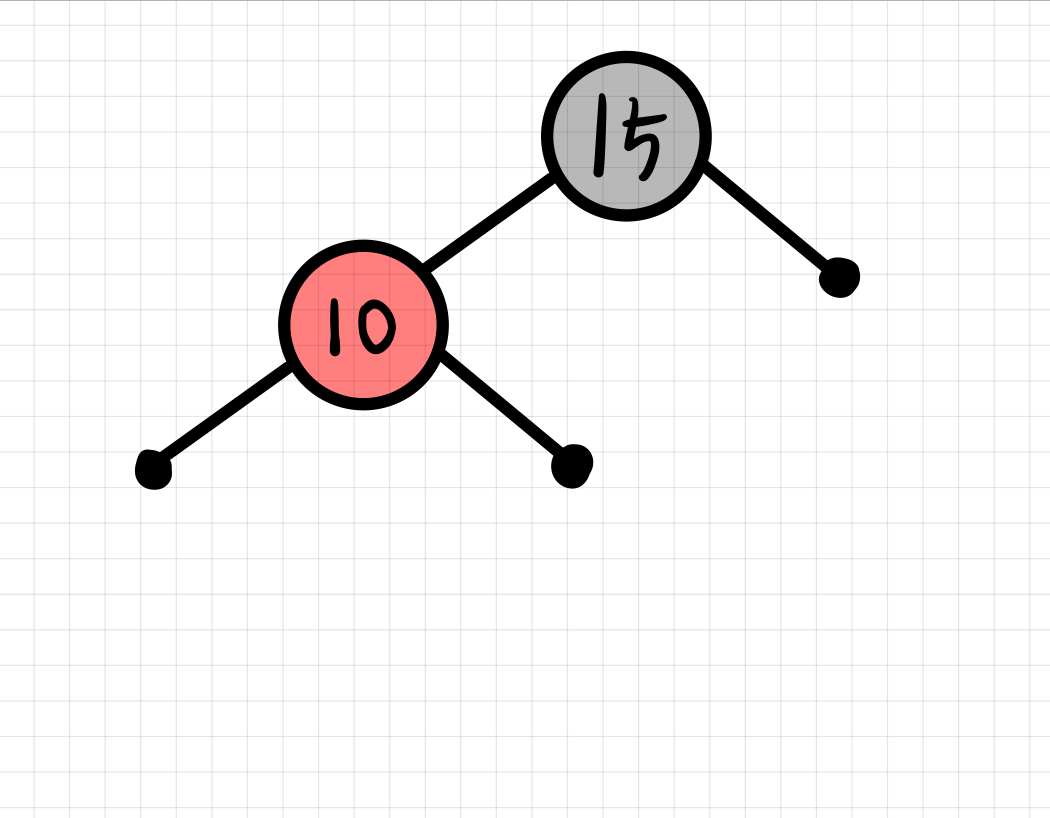
노드 10을 Red로 삽입한 후, 규칙을 점검해봤을 때 모두 만족하기 때문에 삽입을 완료한다.
왜 삽입하는 노드가 RED인가. 🤔
현재 삽입 전 트리는 모든 규칙을 만족하고 있는 RB 트리이다. 새로 삽입하는 노드가 BLACK이면 새롭게 삽입한 노드를 거치는 NIL노드로 향하는 경로와 거치지 않는 NIL노드로 향하는 경로에 있는 BLACK 노드의 수가 달라진다. 따라서 5번 규칙인임의 노드에서 리프 노드(NIL)까지 경로에 있는 BLACK 수가 같다.가 위반되기 때문에 새로 삽입하는 노드의 색깔은 RED여야 한다.
insert(8)
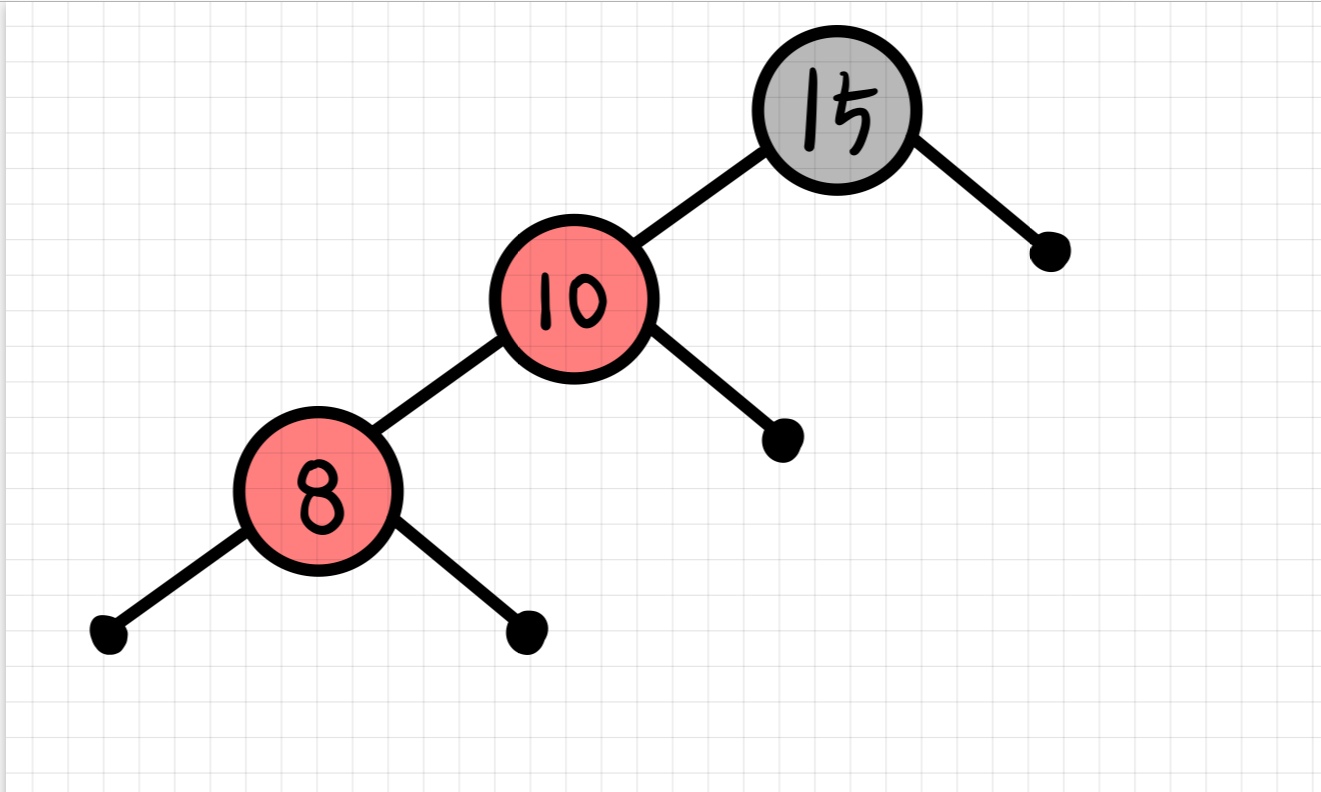
노드 8을 삽입하면, 규칙 3을 위반하기 때문에 트리의 재조정이 필요하다. 10을 기준으로 R-Rotate를 수행하고, 10과 15의 노드 색을 바꾸어주면 완료된다.
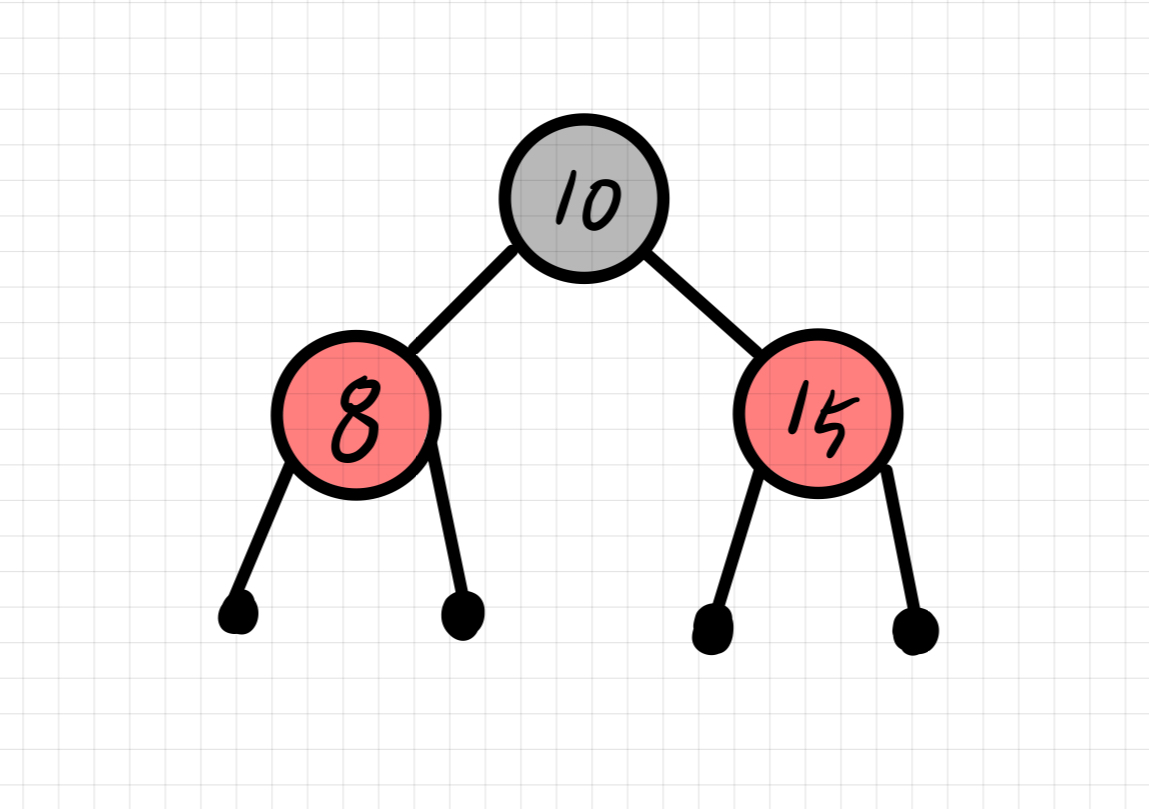
insert(13)
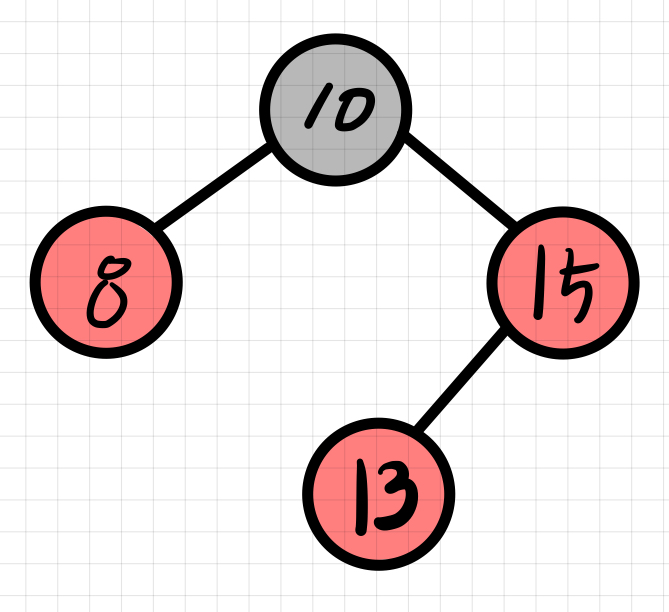
노드 13을 삽입한 후, 규칙 3을 위반하게된다. 8, 15 노드를 Black으로 바꾸고 10노드를 Red로 변경한다.
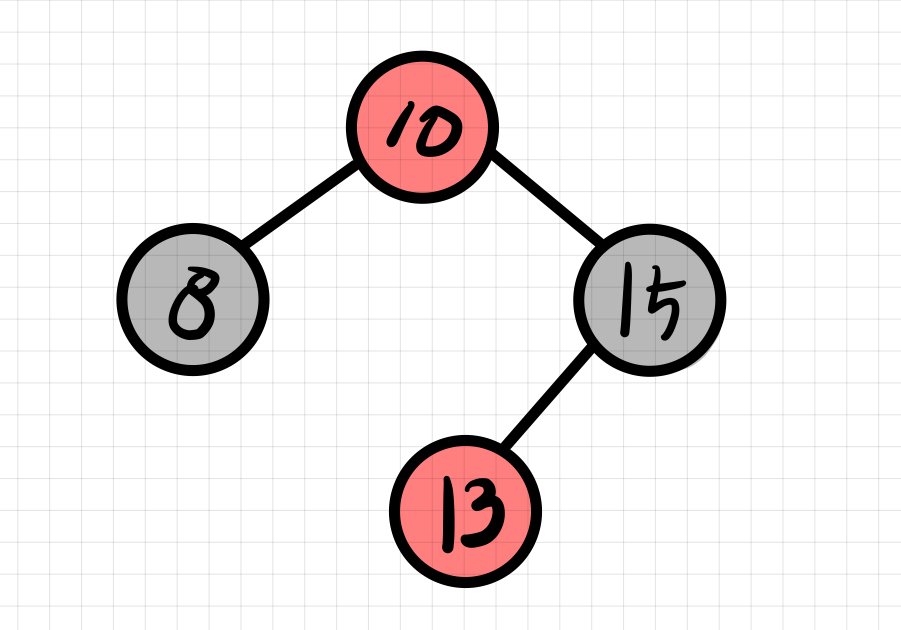
하지만 루트 노드인 10은 Red가 될 수 없기 때문에 Black으로 색상을 변경한다.
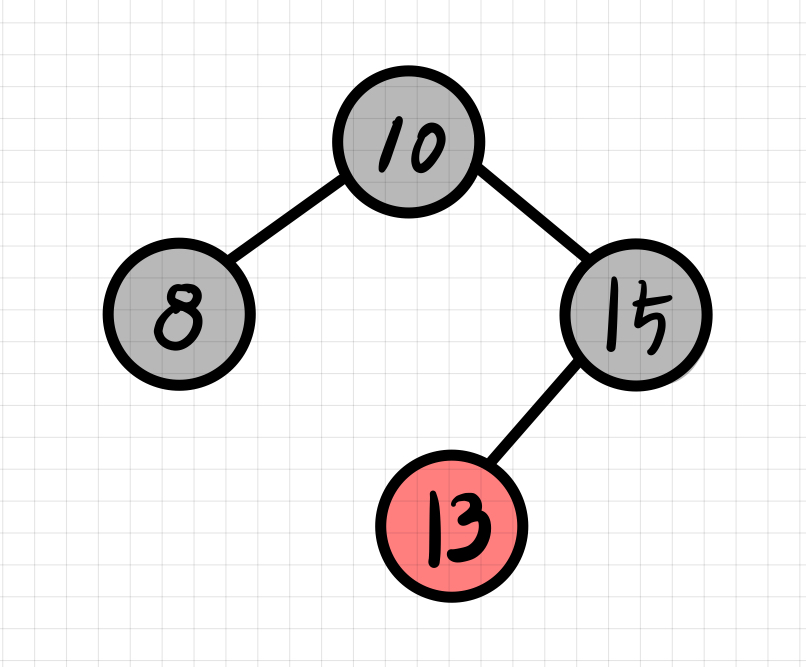
Red-Black Tree 삭제 ( O(log N ) )
- 삭제전 RB 트리 속성을 만족한 상태
- 삭제 방식은 일반 BST와 동일
- 삭제후 RB 트리 속성 위반 확인
- 위반 했다면 재조정
- RB 트리 속성 위반 재확인
삭제 CASE
- 삭제하려는 노드의 자녀가 없거나 하나라면 삭제되는 색 = 삭제되는 노드의 색
- 삭제하려는 노드의 자녀가 둘이라면 삭제되는 색 = 삭제되는 노드의 successor의 색
if. 삭제되는 색이 Red면 어떤 속성도 위반되지 않는다.
else. 삭제되는 색이 Black이면 규칙 2, 4, 5가 위반되는지 확인해야한다.
2번 규칙이 위반되는 경우 - 루트 노드 색을 Black으로 바꾼다.
5번 규칙이 위반되는 경우 - 규칙을 만족시키기 위해 삭제된 색의 위치를 대체한 노드에 Extra Black을 부여한다.
Extra Black을 부여한 노드를 지날때 하나의 black으로 카운트한다.
*doubly black : extra black이 부여된 black 노드
*red-and-black: extra black이 부여된 red 노드
- red-and-black 해결하기
→ red-and-black을 black으로 바꾸면 해결
- doubley black 해결하기
→ doubly black의 형제의 색과 그 형제 자녀의 색에 따라 케이스 분리
Case 4
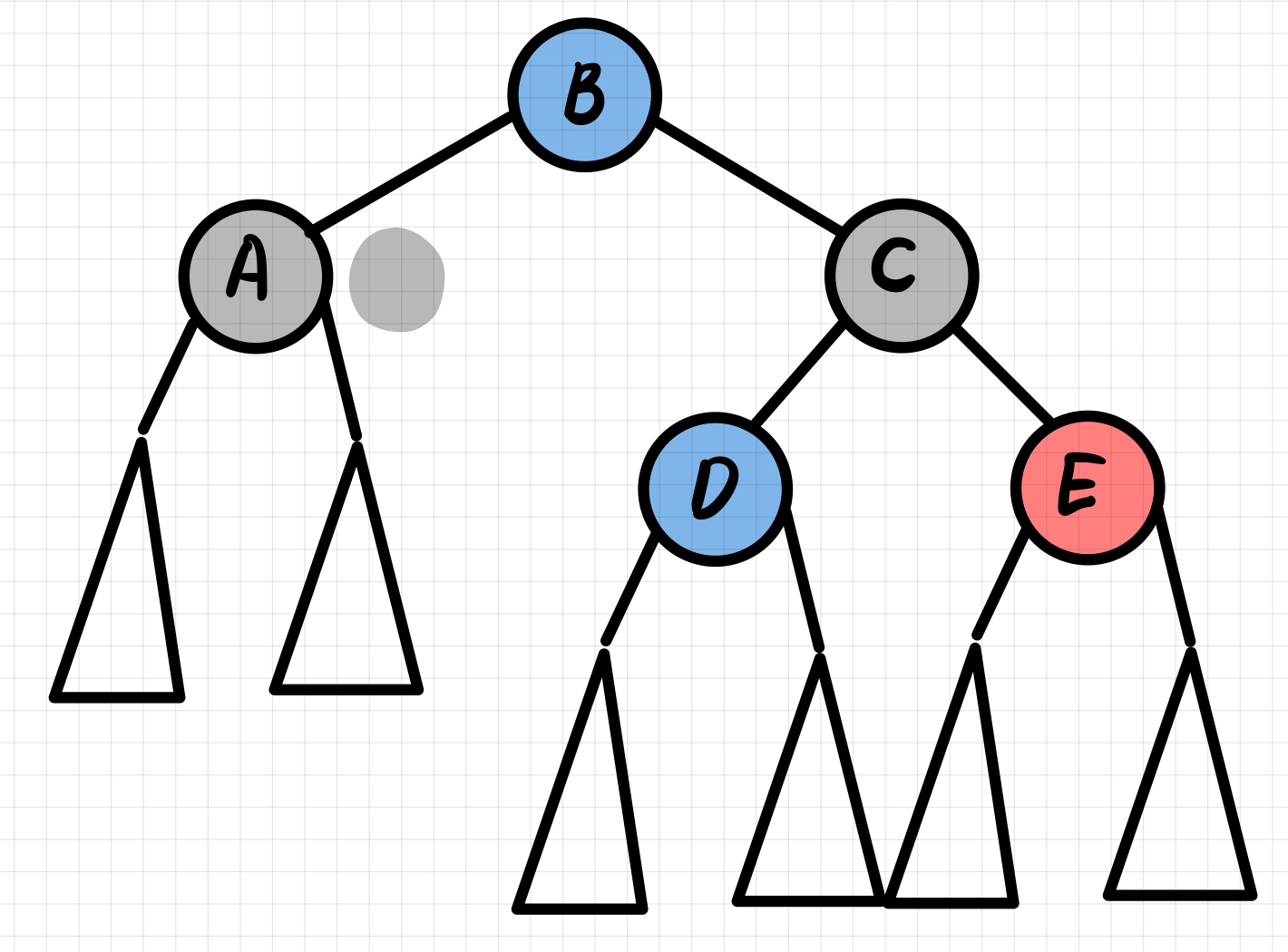 doubly black의 오른쪽* 형제가 black & 그 형제의 오른쪽* 자녀가 red일 때
→ 오른쪽* 형제는 부모의 색으로 오른쪽* 형제의 오른쪽* 자녀는 black으로 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽*으로 회전하면 해결
doubly black의 오른쪽* 형제가 black & 그 형제의 오른쪽* 자녀가 red일 때
→ 오른쪽* 형제는 부모의 색으로 오른쪽* 형제의 오른쪽* 자녀는 black으로 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽*으로 회전하면 해결
Case 3
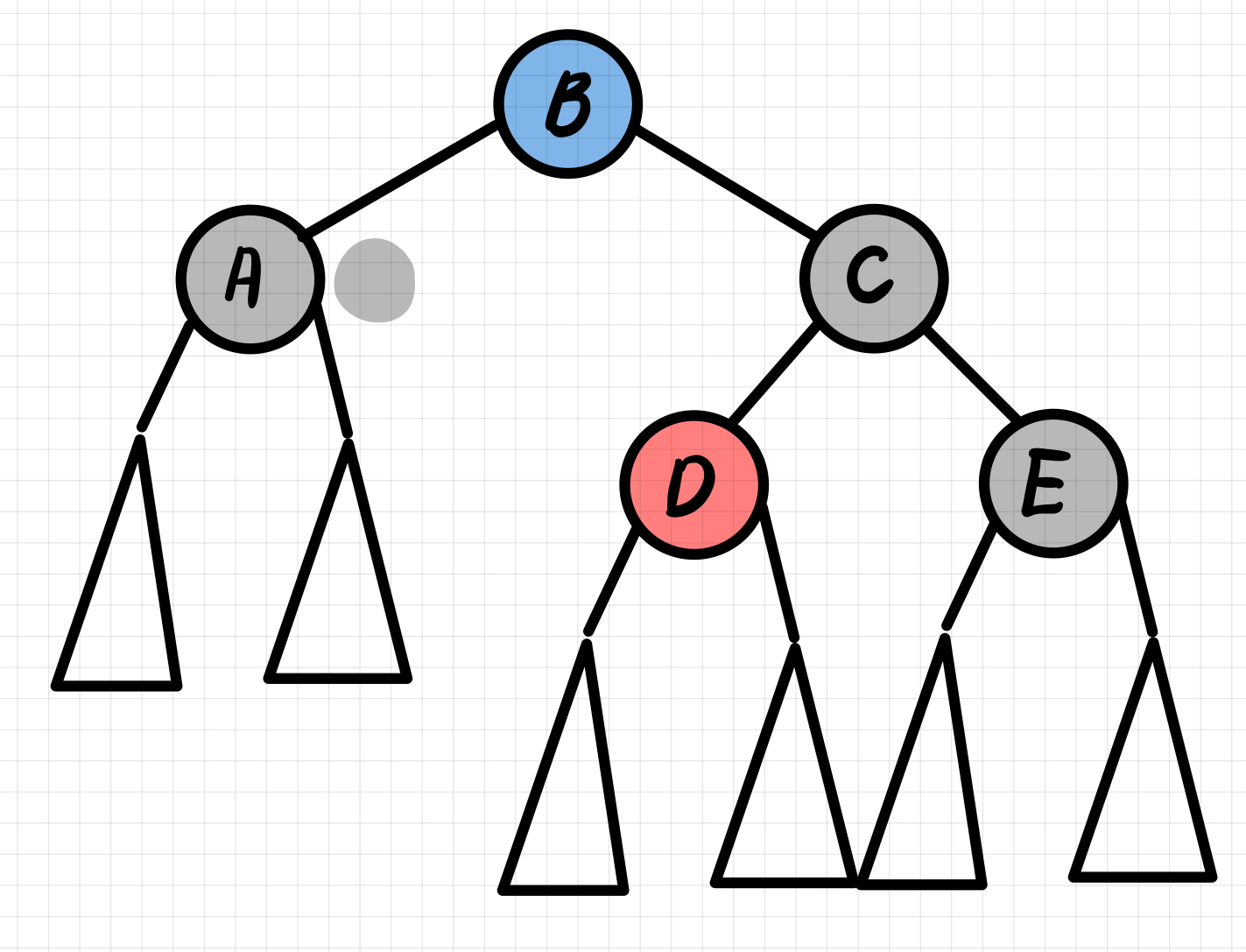 doubly black의 오른쪽* 형제가 black & 그 형제의 왼쪽* 자녀가 red일 때 & 그 형제의 오른쪽 자녀가 Black일 때
doubly black의 오른쪽* 형제가 black & 그 형제의 왼쪽* 자녀가 red일 때 & 그 형제의 오른쪽 자녀가 Black일 때
→ doubly black의 형제의 오른쪽* 자녀가 red가 되게 만들어서 이후엔 case 4 적용하여 해결
Case 2
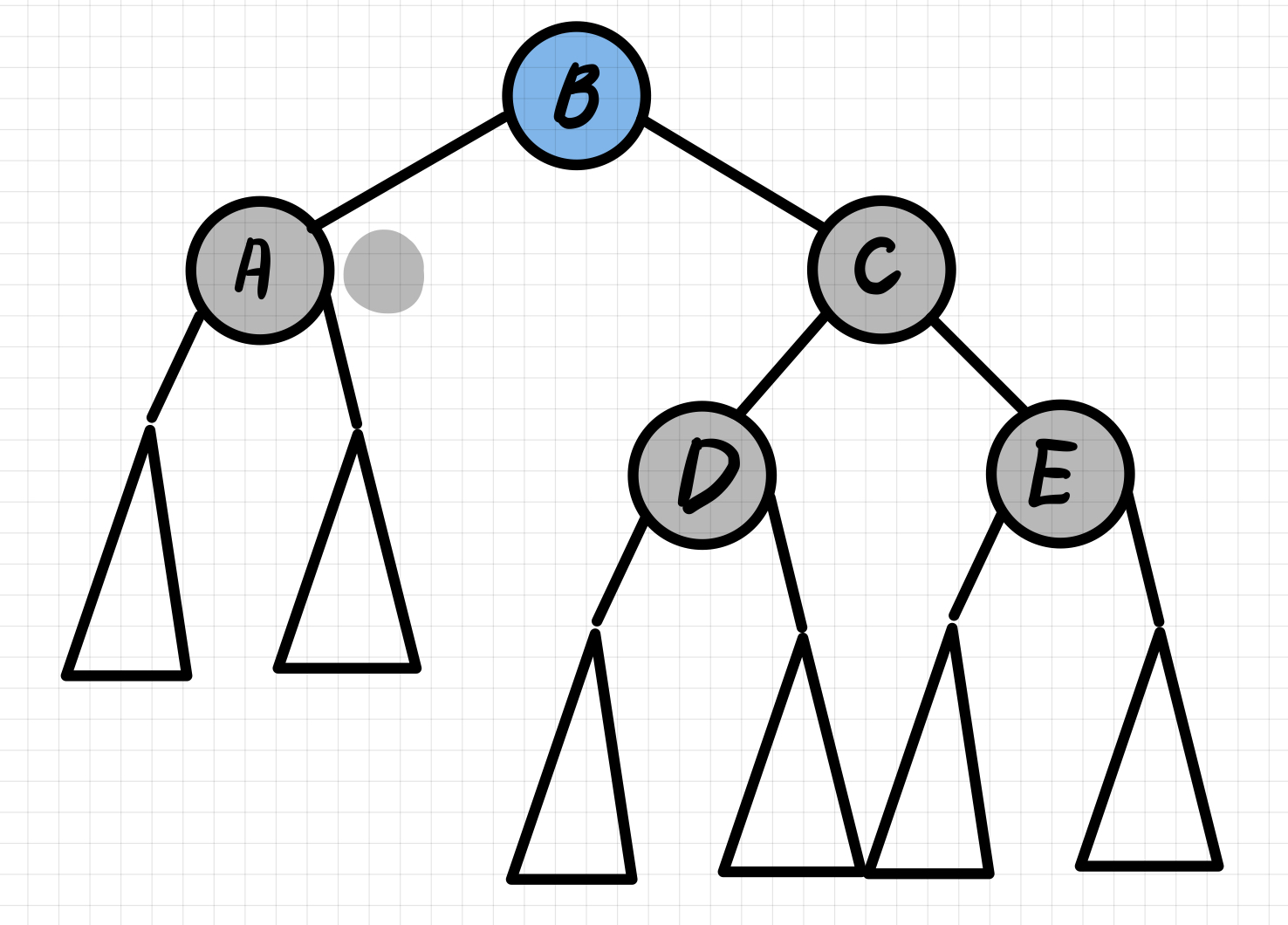 doubly black의 형제가 black & 형제의 양 자식 노드들이 black인 경우
→ doubly black노드와 그 형제 노드의 black을 모아 부모에게 전달, 부모에게 extra black을 해결하도록 위임한다.
doubly black의 형제가 black & 형제의 양 자식 노드들이 black인 경우
→ doubly black노드와 그 형제 노드의 black을 모아 부모에게 전달, 부모에게 extra black을 해결하도록 위임한다.
Case 1
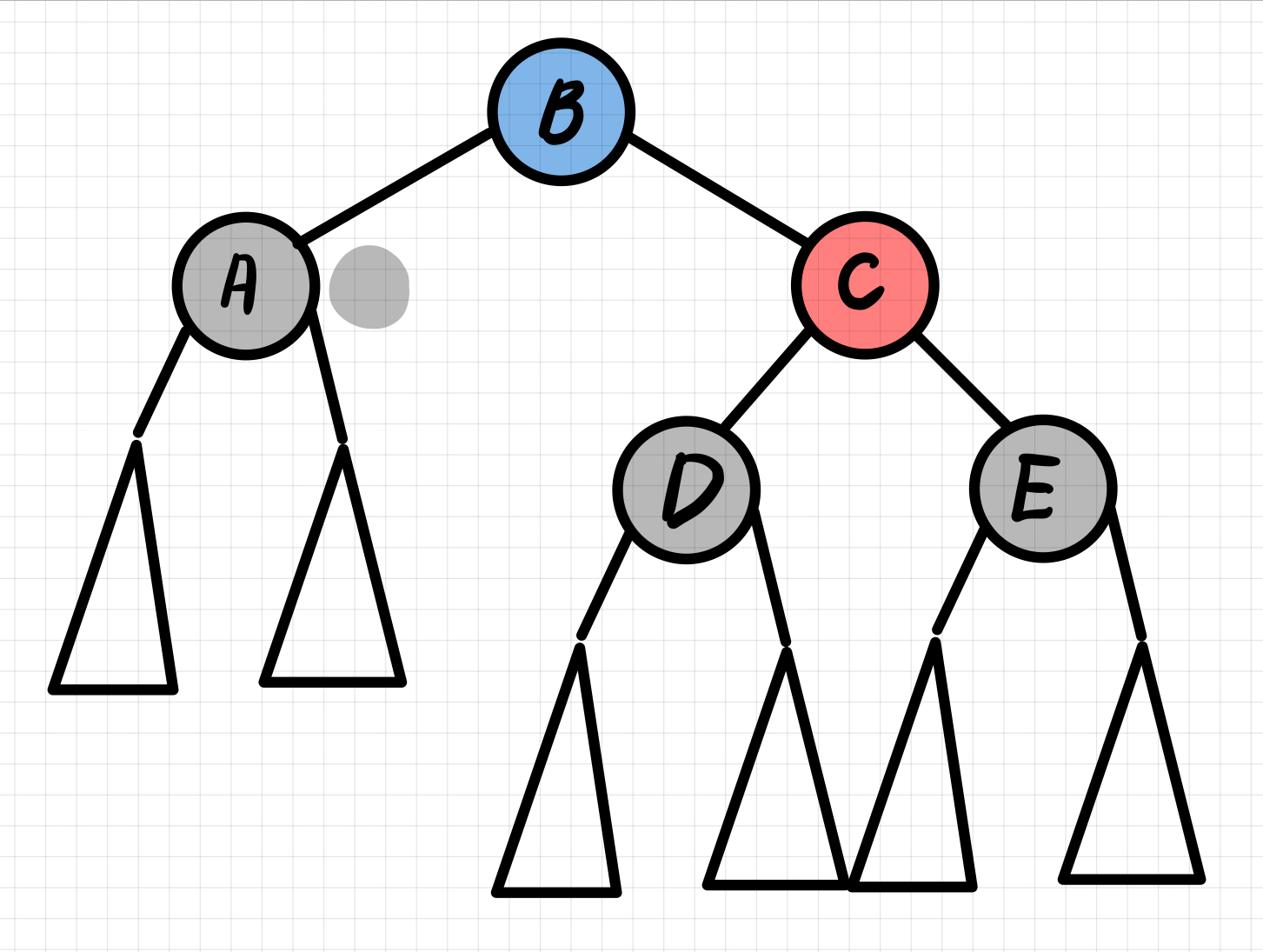 doubly black의 형제가 red일 때
→ doubly black의 형제를 black으로 만든 후, case 2, 3, 4중 하나로 해결
doubly black의 형제가 red일 때
→ doubly black의 형제를 black으로 만든 후, case 2, 3, 4중 하나로 해결