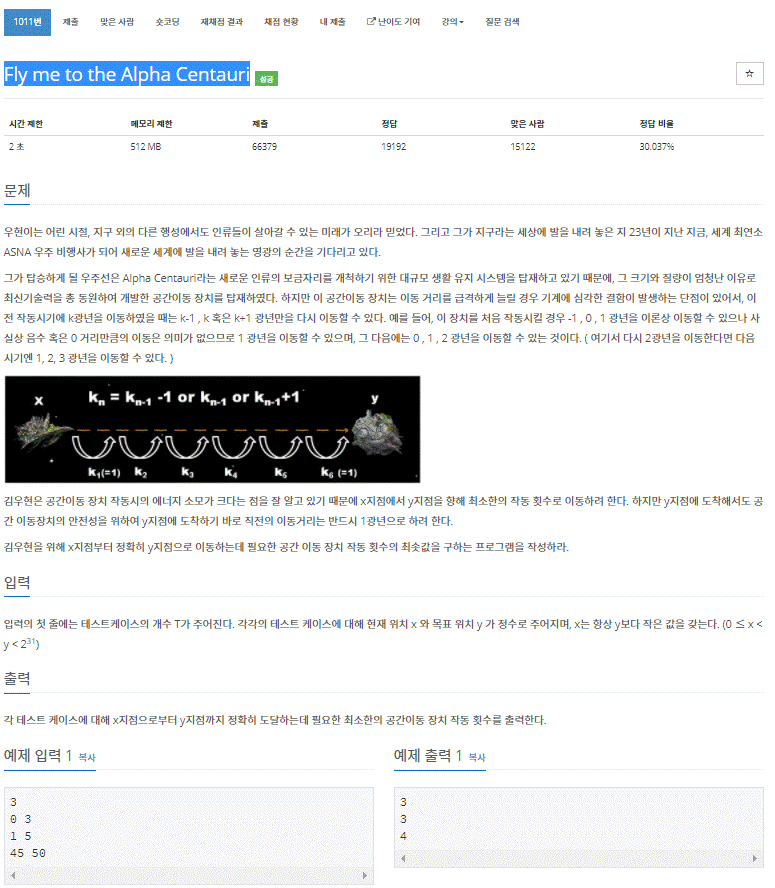
이번 문제는 간단하게 이동 문제였습니다. 주의할 경우는 이동할 수 있는 거리가 k광년 기준으로 k-1, k, k+1이며 음수 혹은 0으로는 이동하지 않습니다.(의미가 없다고 계산 자체를 안하는거 같습니다.) 쉽게 이동거리만 이야기하면 한번에 10 광년을 이동할 수 없으므로 1 > 2 > 3 > 4 > 5...이런 식으로 +1만큼 증가 혹은 감소 하면서 이동이 가능합니다. 또한 조건에 마지막에는 1광년으로만 이동해야한다는 조건이 있습니다. 이는 예를 들어 0광년에서 15광년을 가야하는 경우 0 > 1(1증가) > 3(2증가) > 6(3증가) > 10(4증가) > 13(3증가) > 15(2증가) 이런 식으로 적절한 시기에 이동거리를 줄이지 않으면 마지막에 +1광년을 맞출 수 없습니다. 그리고 최소 이동 횟수를 구하는게 목적입니다. 또한 문제를 풀다 보면 간과하기 쉬운 점이 굳이 증가나 감소 없이 현재 거리를 유지해도 된다는 점입니다.
Step 0.해답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Fly_me_to_the_Alpha_Centauri_1011 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine()); // 테스트 반복 횟수
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
System.out.println(searchK(Integer.parseInt(st.nextToken()),Integer.parseInt(st.nextToken())));
}
}
public static int searchK(long x, long y){
long n = 0; //이동 거리
int count = -1; // 횟수 카운팅
long sum = 0; // n + 1의 까지의 합.
long before_sum = 0; // n까지의 합
for (long i = x; i <= y; i = i + n) {
sum = (n + 1) * (n + 2) / 2;
before_sum = n * (n + 1) / 2;
if (sum <= y - i) {
n += 1;
} else if (before_sum <= y - i) {
n = n;
} else if (n != 1){
n = n-1;
}
before_sum = 0;
sum = 0;
count++;
}
return count;
}
}문제를 처음 봤을 때는 오래 걸릴줄 알았는데 의외로 별 문제 없이 금방 풀어진 문제였습니다.
주의할 점이라면 변수 타입입니다. 입력 받는 숫자는 int타입이어도 상관은 없는듯 하나 일단 문제 범위 자체로는 int 범위를 넘는거 같습니다.
지금 보니 범위가 <이었습니다. 2^31이면 딱 int범위에서 1만큼 벗어나는데 미만이기에 딱 int범위였습니다.
또한 변수 설정에서 이동 거리는 sum값을 구하다 보면 sum 값이 int범위를 벗어나서 long타입으로 줬습니다. sum과 before_sum도 비슷한 맥락으로 long타입으로 변수선언을 하였습니다.
Step 1. 문제 접근
위에서 작성하였듯이 이 문제는 최소 이동 횟수를 구해야 하면서 동시에 마지막에는 1광년 만큼만 이동해야 합니다. 즉 저희는 어느 정도까지는 계속 이동 거리를 +1로 늘려주다가 적절한 시기에 이동 거리를 줄여주거나 유지하면서 마지막에는 +1 광년을 만들어줘야 합니다. 이를 위해서 저는 1~n+1까지의 합(sum과 before_sum)을 구하는 식과 도착 지점과 시작 지점의 차를 사용하였습니다.
Step 2. 문제 해결
저는 값이 최대치까지 증가하다가 최고점에서 유지 혹은 감소를 하도록 하였습니다. 즉 제가 구할 값은 크게 1. 속도 +1 2.속도 유지. 3. 속도 -1 입니다.
1. 문제에서 테스트 횟수와 이동해야할 거리를 입력받습니다.
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine()); // 테스트 반복 횟수
for (int i = 0; i < T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
System.out.println(searchK(Integer.parseInt(st.nextToken()),Integer.parseInt(st.nextToken())));
}
}이때 Long형으로 받는 이유는 입력 범위가 딱 int범위를 벗어나는 부분까지이기 때문이었는데 int형으로 입력을 받아도 통과가 되는걸로 봐서는 실질적으로 int범위 밖의 수는 입력을 하지 않은듯합니다.
지금 보니 입력은 int범위에 딱 맞게 설정되어 있었습니다.
2. 변수 초기화 및 이동거리 탐색을 위해 for문을 선언합니다. 또한 1~n까지의 합을 구하기 위해 sum, before_sum 변수에 수식을 대입해줍니다.
long n = 0; //이동 거리
int count = -1; // 횟수 카운팅
long sum = 0; // n + 1의 까지의 합.
long before_sum = 0; // n까지의 합
for (long i = x; i <= y; i = i + n) {
sum = (n + 1) * (n + 2) / 2;
before_sum = n * (n + 1) / 2;sum 함수는 1~n+1까지 더한 합이고 before_sum은 1~n까지의 합입니다. 예를 들어 n이 5라면 1 + 2 + 3 + 4 + 5 => 15입니다. 이 sum들을 구한 이유는 거리를 줄이거나 유지해야하는 경계선을 찾기 위해서입니다. 식은 1~n까지의 합 기준으로 n * (n + 1) /2입니다. 처음에는 제귀함수를 이용해서 풀어봤는데 시간 초과로 수식을 찾아서 풀었습니다. for문의 x는 시작 거리, y는 도착 거리까지 이며 증감식에서는 현재 거리 + 이동거리를 해주어서 현재 위치를 i로 나타냈습니다. 여기서 i의 값이 변해도 괜찮은 이유는 for문에서는 변수 초기화가 처음 한 번만 일어나므로 i 값을 바꾼다고 for문의 흐름이 바로 바뀌지는 않기 때문입니다.
3. if문을 사용해서 남은 거리(y - i)가 sum보다 같거나 크면 이동 거리를 계속해서 1 늘려줍니다.
if (sum <= y - i) {
n += 1;
}y는 도착 지점, i는 현재 위치입니다. 즉 y-i는 남은 거리가 됩니다. if문을 보면 남은 거리가 1~n+1인 sum보다 같거나 클 경우 이동거리인 n을 1씩 늘려주는걸 볼 수 있습니다. 여기서 sum 값의 의미는 예를 들어서 설명해보자면 현재 n이 4인 경우 sum은 1~5까지의 합인 15를 구합니다. 여기서 남은 거리가 15보다 크거나 같다면 당장에 다음 이동에서 n의 값은 1 늘려줘도 괜찮다는 이야기입니다. 좀 더 쉽게 말해보자면 sum을 풀어쓰면 1 + 2 + 3 + 4 + 5가 됩니다. 여기서 남은 거리가 딱 15라면 다음 칸에 +1만큼 더해서 5광년을 이동하고 그 다음엔 4, 3, 2,1광년을 이동하게 되면 딱 15광년이 나오게 됩니다.
4. 속도가 증가하는 경우를 구했으므로 다음은 속도를 유지하는 경우를 구하였습니다.
else if (before_sum <= y - i) {
n = n;
}남은 거리가 1~n까지의 합인 before_sum보다 같거나 크다면 이동거리 n을 유지해줬습니다. 예를 들어 설명해보자면 남은 거리가 10인 상황에서 n은 현재 4입니다. sum값은 15이므로 다음 칸에 n을 5로 늘려버리면 마지막에 +1을 해줄 수 없습니다. 그러면 이제 before_sum을 확인해봅니다. before_sum은 1~4까지의 합인 10이므로 다음 칸에 현재 속도인 4를 입력하면 4 > 3 > 2 > 1로 남은 10광년을 마지막에 1광년만큼 이동하면서 도착이 가능해집니다.
5. 마지막으로 현재 속도가 1이 아니라면 속도를 감속시켜줍니다.
else if (n != 1){
n = n-1;
}
before_sum = 0;
sum = 0;
count++;
}
return count;
}위의 if문과 else if문들을 통해 거리의 여유가 있는 경우들은 전부 걸러진 상황입니다. 이제 남은 여유가 없는 수들밖에 남지 않았기에 속도를 줄여줘야 하는 상황인 것입니다. 여기서 주의할 점은 문제에서 음수나 0만큼 이동은 의미가 없다고 하였기에 n != 1의 조건을 줘야한다는 것입니다. 0을 따로 조건식에 주지 않은 이유는 n은 무조건 1을 한번은 달성하게 되기 때문입니다. 그렇기에 1이상인 n값을 계속 줄일 경우 n != 1만 해주면 자연스럽게 0도 걸러지게 됩니다. 조건에 맞을 경우에는 속도를 1씩 줄여주며 마지막에는 변수 초기화 및 횟수를 1만큼 늘려주고 for문이 끝나면 count를 return 해줬습니다. 여기서 else문을 따로 만들어서 n=n을 하지 않은 이유는 위의 경우에 포함되지 않을 경우에는 for문의 증감식에 의해서 자동으로 n은 쓰였던 값을 그대로 들고 오기 때문입니다.
Step 3. 느낀 점
처음 그림이랑 설명만 봤을 때는 이게 무슨 문제인가 했는데 차근차근 정리를 하고 풀어보니 의외로 어렵지 않은 문제였습니다. 이번 문제를 통해 알고리즘을 짜는 틀을 만드는 능력을 기를 수 있었던거 같습니다. 그리고 의외로 빨리 풀어서 문제가 맞았을 때는 기분이 더 좋았던거 같습니다.
출처 : 백준 1011번 https://www.acmicpc.net/problem/1011