이번 문제는 아파트의 k층 n호에 몇 명이 사는지를 구하는 문제였습니다. 또한 1층이 아닌 0층부터 시작을 합니다.
조건으로는 각 층에 사람이 살지 않는 호는 존재하지 않으며 자신이 b호라고 한다면 자신의 아래층의 1호 ~ b호까지 합만큼의 사람이 b호에 살아야 합니다.
Step 0. 해답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class V_President_2275 {
public static int search_N(int k, int n) {
int[] apt_1 = new int[n]; // 첫 층
int[] apt_2 = new int[n]; // 다음 층
for (int i = 1; i <= n; i++) { // 1층의 1~n명을 전부 넣어줌.
apt_1[i - 1] = i;
}
if (k == 0) {
return apt_1[n - 1];
}
apt_2[0] = 1;
for (int i = 1; i <= k; i++) {
for (int j = 1; j < n; j++) {
apt_2[j] = apt_2[j - 1] + apt_1[j];
}
apt_1 = apt_2.clone();
}
return apt_2[n - 1];
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
int k = 0; // 층
int n = 0; // 호
for (int i = 0; i < T; i++) {
k = Integer.parseInt(br.readLine()); // 층
n = Integer.parseInt(br.readLine()); // 호
System.out.println(search_N(k, n));
}
}
}
별 어려움 없이 풀 수 있었던 문제였습니다. 괜히 무슨 식이 존재하지 않을까 1시간 정도 찾아봤는데 끝내 찾지 못하고 정공법으로 풀었습니다. 찾아보니 푸는 방법은 결국 다 비슷한데 방식이 틀린 분이 계셨습니다. 그 중 가장 인상 깊었던 것은 재귀함수를 이용한 방법이었습니다.
Step 1. 문제 접근
저는 호를 표현할 때 YX호라고 표현하겠습니다. Y는 층수이며 X는 몇 번째 칸인지입니다. X는 0보다 작은 값이면 십의 자리에 0을 넣어 표현했습니다.(001호, 103호, 1112호..)
문제 접근 전 사진 한 장 보여드리겠습니다.
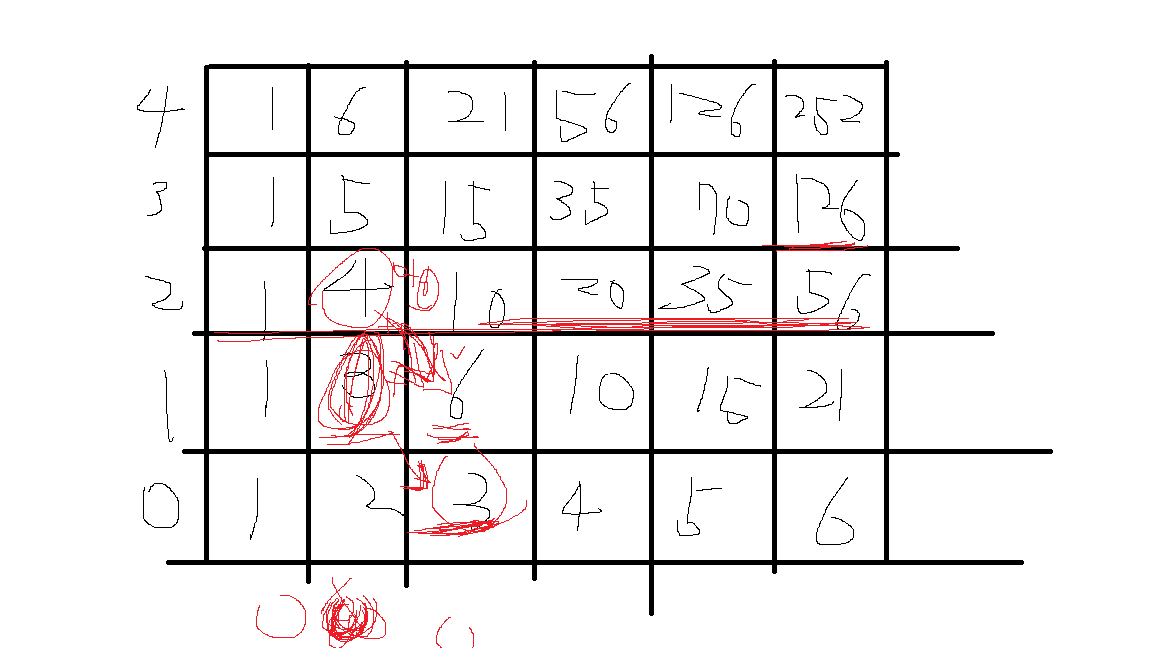
많이 난잡하지만 무슨 식이나 특출난 관계성이 존재하지 않을까? 싶어서 표를 그려두고 빨간 펜으로 끄적인 사진입니다. 별다른 식이나 특출난 관계성을 찾진 못하였기에 정공법으로 풀었습니다. 1층은 1~N까지의 숫자가 들어갈 것입니다. 각 층의 첫 칸은 자신이 첫 칸이기에 더해줄 값이 없으므로 밑에 층의 인원인 1명이 들어가는 것을 볼 수 있습니다. 그 이후의 칸들은 1층을 예로 들어보면 102호는 3명이 사는데 이는 101호에 002호를 더한 값입니다. 104호를 보면 103호인 6명 + 004호인 4명 해서 총 10명이 있는것을 볼 수 있습니다. 이것을 식으로 사용하여 문제를 풀었습니다.
Step 2. 문제 해결
search_N메서드를 만들어서 문제를 풀었습니다.
1. 메인 메서드에서 BufferedReader를 사용하여 입력을 받았습니다. BufferedReader를 사용하였기에 throws를 통해 IO예외를 해줬습니다. 그 후 int T, k, n을 이용해서 테스트 반복 횟수, 층, 호의 값을 받아 for문을 사용하여 테스트 횟수 T만큼 반복해주면서 search_N메서드를 호출 및 프린팅 해주었습니다. k, n값은 String으로 받기 때문에 int형으로 바꿔주는 작업도 하였습니다.
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
int k = 0; // 층
int n = 0; // 호
for (int i = 0; i < T; i++) {
k = Integer.parseInt(br.readLine()); // 층
n = Integer.parseInt(br.readLine()); // 호
System.out.println(search_N(k, n));
}2. k, n은 각각 메인 메서드에서 층, 호를 입력 받았습니다.
- 저는 배열 2개를 생성하였습니다. 두 개의 층으로 구성한 이유는 값을 계산하기 위해선 위의 문제 접근에서 말씀드렸다시피 현재 층 n - 1의 값과 밑에 층 n호의 값이 필요합니다. 즉, 원하는 값을 구하기 위해선 2개의 층에서 값을 가져와야 했습니다. 이 2개의 층을 통해 0, 1층을 구하고 1층을 통해 2층을, 2층을 통해 3층을 구하는 식으로 원하는 층 까지 구했습니다.
public static int search_N(int k, int n) {
int[] apt_1 = new int[n]; // 첫 층
int[] apt_2 = new int[n]; // 다음 층각 배열의 크기를 n만큼 주고 생성해줍니다. 또한 apt_1배열은 첫 층, apt_2는 다음 층으로 하였습니다.
3. 첫 층은 1명~n명이 존재하기에 for을 사용해서 apt_1에 값들을 대입해줬습니다.
for (int i = 1; i <= n; i++) { // 1층의 1~n명을 전부 넣어줌.
apt_1[i - 1] = i;
}
if (k == 0) {
return apt_1[n - 1];
}
apt_2[0] = 1;이때 층이 0층일 경우는 바로 값을 return해줬고 apt_2의 경우, 위에서 설명했듯이 모든 층의 첫 칸은 1이기 때문에 1을 넣어줬습니다.
4. apt_1은 0층의 값을 넣어줬으니 apt_2도 구해줬습니다. apt_2는 다음 층이면서 동시에 저희가 마지막에 찾게 될 k층입니다. 우선 0층을 기준으로 apt_2는 1층이 되고 각 층에 값들을 for문의 j 변수를 이용해 넣어줬습니다. 이때 첫 칸은 1로 값을 주었기 때문에 다음 칸 부터 값을 넣었습니다. 그 후 다음 층인 2층의 값을 구해야 하기 때문에 apt_1에 apt_2를 깊은 복사 해줬습니다.그 후 apt_1에 깊은 복사로 저장된 1층의 데이터를 사용하여 2층인 apt_2에 새롭게 데이터를 업데이트 해줬습니다. 이렇게 한 층씩 올라가서 원하는 k층에 도달하면 해당 층의 n호 값을 apt_2[n-1]을 해주어 리턴해줬습니다.
for (int i = 1; i <= k; i++) {
for (int j = 1; j < n; j++) {
apt_2[j] = apt_2[j - 1] + apt_1[j];
}
apt_1 = apt_2.clone();
}
return apt_2[n - 1];
}
Step 3. 느낀 점
문제를 들여다보면서 생각을 많이 해본 시간이었습니다. 결국 뭔가 특출난 식이 존재하진 않는다는 걸 끝에서야 알았지만 그래도 생각을 열심히 한 나쁘지 않았던 시간 같습니다. 또한 제가 푼 것은 아니지만 제귀함수를 통한 풀이도 보면서 오랜만에 제귀함수를 다시 볼 수 있었고 문제에 대한 접근 방법의 다양성도 향상시킬 수 있었던 시간입니다.
출처 : 백준 2775번 https://www.acmicpc.net/problem/2775