Self Number
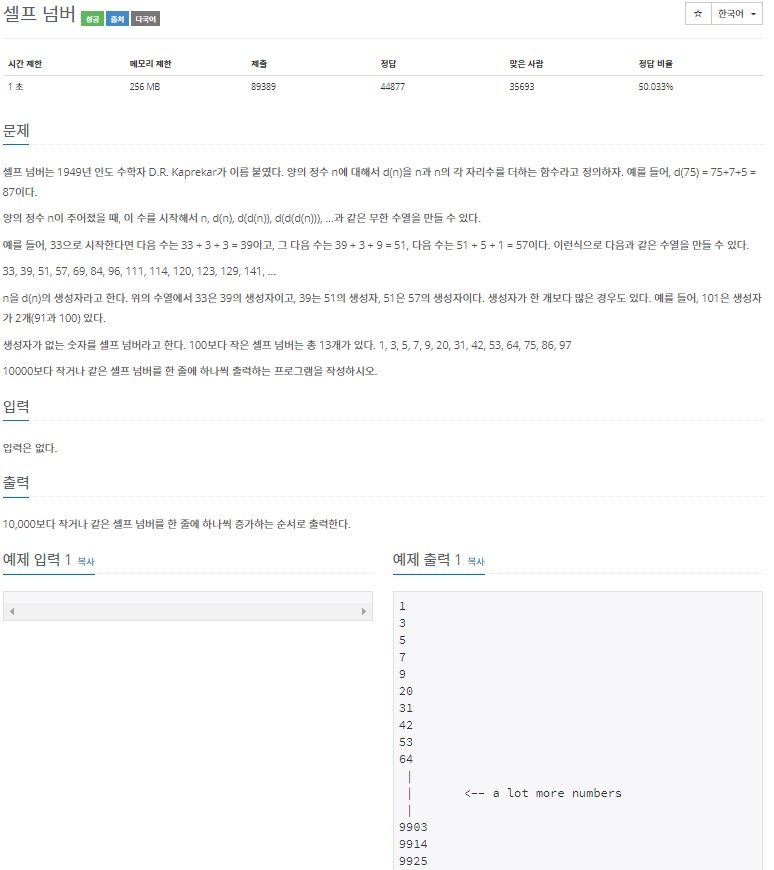
이번 문제는 셀프 넘버라는 수학식이었습니다. 기본 설명은 사진으로 생략하고 어떤 방식으로 풀지 열심히 생각해 봤습니다.
import java.util.Arrays;
public class SelfNumber_4673 {
public static void main(String[] args) {
Integer[] non_self_num = new Integer[10000]; // SelfNumber들을 저장해줄 배열 생성 - Arrays.asList.contains 때문에 기본타입인 int는 사용 불가능.
for (int i = 0; i < 10000; i++) {
String[] calcul_self = Integer.toString(i + 1).split(""); //숫자를 입력 받으면 일의 자리, 십의 자리, 백의 자리..등으로 나누어서 배열에 저장해 줌.(10은 "1","0" 951은 "9","5","1"..String형으로)
int self = i + 1; //non_self_num배열에 저장해줄 숫자.
for (int j = 0; j < calcul_self.length; j++) { //1~9까지는 1번, 10~99까진 2번. 100~999까지는 3번.. 자릿수에 따라 for문 실행
self += Integer.parseInt(calcul_self[j]); // 입력한 숫자 원본 + 일의 자리 + 십의 자리 + 백의 자리... 계산 해줌
}
non_self_num[i] = self; //계산된 non_self_num를 non_self_num배열에 차곡차곡 쌓아줌.
// if (!Arrays.asList(non_self_num).contains(i + 1)) { 주석 처리됨.
// System.out.println(i + 1);주석 처리됨.
// }주석 처리됨.
}
for (int g = 0; g < 10000; g++) { //Arrays.aList.contains를 사용하여 문제에서 원하는 셀프 넘버가 아닌 수를 찾음
if (!Arrays.asList(non_self_num).contains(g + 1)) {
System.out.println(g + 1);
}
}
}
}일단 풀이 방식은 1~10000의 범위가 주어졌기에 10000크기의 배열을 만들어서 셀프 넘버가 아닌 수를 구해서 전부 넣어주고 이 배열에 없는 수, 즉 셀프 넘버만을 찾아 출력해 주었습니다.
이때 처음 숫자를 입력받으면 toString.split을 사용해서 문자열로 나누어서 일의 자리, 십의 자리, 백의 자리 이런 식으로 하나씩 떼어 줬습니다. 여기서 아쉬운 점은 나중에 생각한 건데 그냥 나누기를 해가지고 나머지를 찾았으면 더 편하지 않았을까.. 라는 점입니다. 그런 다음 각 자리의 문자열로 변한 수를 갖고 원래의 수 + 각 자리의 수(문자를 int로 바꿔줘서)를 더해서 non_self_num을 찾고 배열에 저장한 후 최종적으로 셀프 넘버를 찾았습니다.
그리고 마지막에 contains를 사용할 경우 기본형인 int는 사용 불가능하기에 Integer를 사용해 주었습니다!
다 하고 나서 보니 String[] calcul_self = Integer.toString(i + 1).split(""); 이 부분이 배열에 따로 초기 크기를 지정해 주지 않고 잘 쓴 거 같아서 신기했습니다.
중간에 주석 처리 됨 이라고 써둔 if문은 맨 밑의 for문을 없애고 저렇게 써본건데 쓰고 나서 보니 원래 방식은 처음에 non_self_num을 10000번 저장해 주고 나중에 셀프 넘버 찾을려고 10000번만 for문을 돌리면 됐는데 괜히 잔머리 써서 주석처리 됨 부분처럼 넣어주고 생각해 보니 if를 저렇게 주면 나중에는 1~9000번 배열까지 확인하고 그다음은 1~9001번 확인하고.. 이런 식으로 오히려 더 안 좋은 코드가 되었습니다. 저렇게 풀고 백준에 올려봤는데 오히려 메모리랑 속도가 안 좋아져서 생각해 보니 그렇더라고요! 배운 것도 많고 생각한 것도 많은 문제였습니다. 아래 사진의 밑에는 맨 밑에 for문 쓴 거고 위에는 맨 마지막 for문을 뺀 코드였습니다.

그래도 다 풀고 다른 분들 코드 보니 훨씬 좋고 속도도 많이 차이 나면 2배~10배까지도 차이 나는 거 보고 아직 할게 많구나 생각했습니다.
출처 : 백준 4673번 https://www.acmicpc.net/problem/4673