코딩테스트를 풀 때 재귀용법 문제가 나오면 항상 제대로 풀지 못했던 기억이 나서 재귀용법을 써서 풀어야 하는 문제를 풀어보았다. 3시간 동안 고민했지만 풀이가 떠오르지 않아서 다른 사람들의 풀이를 이해하려고 노력했다. 그런데 다른 사람 풀이를 봐도 이해가 안가서 하루동안 고민하고 이해한 내용을 토대로 다시 문제를 풀어보았다.이 문제를 풀어보면서 재귀용법을 사용하기 위해서는 탑다운 방식으로 사고하는 것이 필요하다는 것을 체감했다.
1. 문제
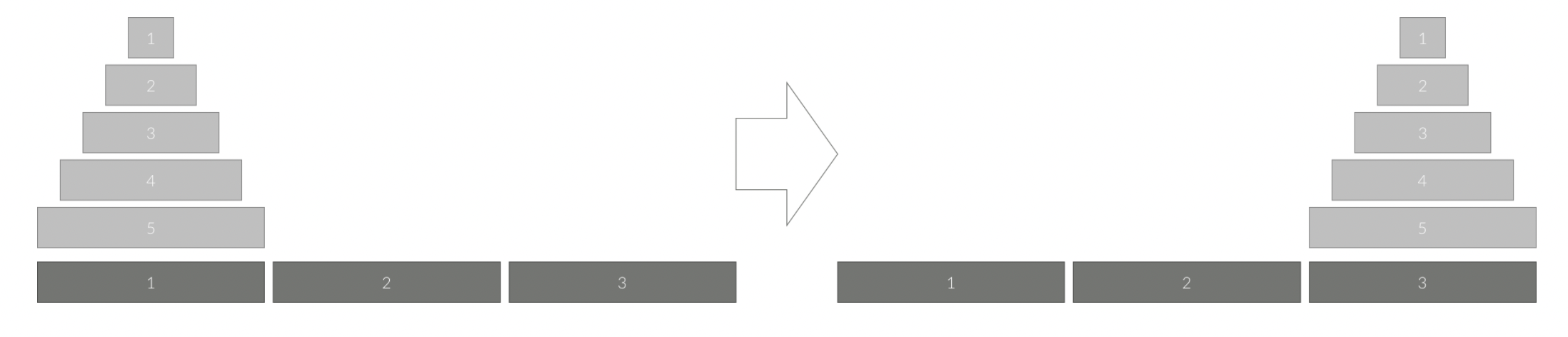
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
2. 풀이
이 문제는 재귀용법으로 풀어야 한다. 그리고 재귀용법은 탑다운 방식으로 사고해야한다.
그래서 가장 큰 원판이 움직이는 상황을 생각해보자.
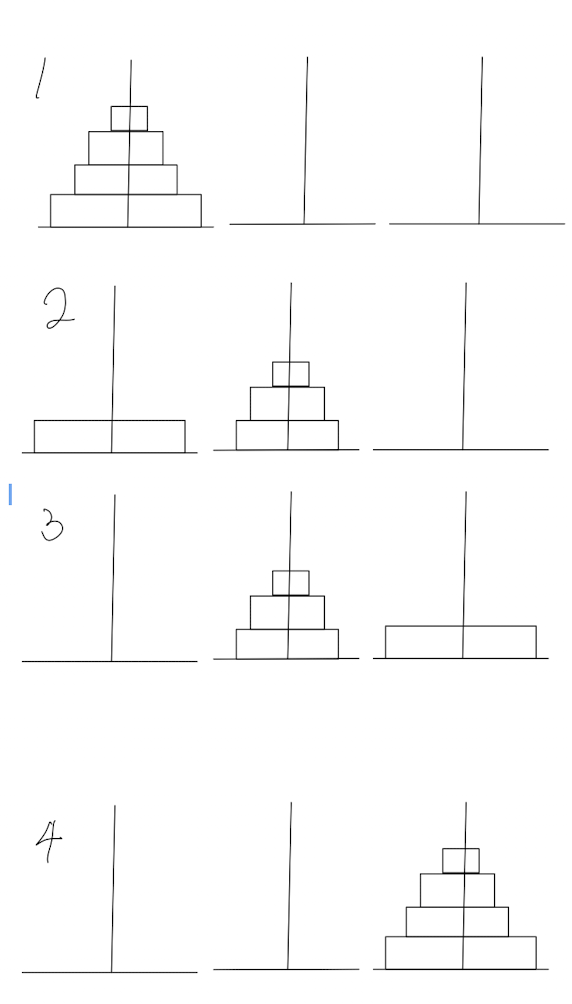
1. 처음 상태
- 옮겨야 할 원판 : 4개
- 1번 기둥 => 3번 기둥
2. 가장 큰 원판을 한 번만 옮기면 되는 상황
- 옮겨야 할 원판 : 3개
- 1번 기둥 => 3번 기둥
3. 가장 큰 원판을 옮긴 상황
4. 나머지 원판들을 가장 큰 원판 위로 옮기는 상황
- 옮겨야 할 원판 : 3개
- 2번 기둥 => 3번 기둥
위의 상황을 일반화 하면 n개의 원판을 가진 기둥을 옮기려면 n-1개의 원판을 옮기는 것을 한번 한 뒤 가장 큰 원판을 옮기고 n-1개의 원판을 옮겨야 한다.
1. n-1 개의 원판을 출발지에서 (출발지와 도착지가 아닌 나머지 기둥)으로 옮긴다.
2. 가장 큰 원판을 도착지로 보낸다.
3. n-1 개의 원판을 (출발지와 도착지가 아닌 나머지 기둥)에서 도착지로 옮긴다.이를 아래와 같이 코드로 나타낼 수 있다.
result = []
def hanoi(n, f, b, t):
if n == 1:
result.append([f,t]) # 원판이 하나만 남았을 때는 가야할 곳으로 바로 갈 수 있다.
else:
hanoi(n-1, f, t, b) # 1. 옮겨야 할 가장 큰 원판이 한번만 움직여도 될 때를 만들어주는 상태
result.append([f,t]) # 2. 옮겨야 원판 중 가장 큰 원판을 옮김
hanoi(n-1, b, f, t) # 3. 가장 큰 원판을 옮긴 뒤에는 나머지 원판들을 그 위로 옮김
n = int(input())
print(2**n - 1)
hanoi(n, 1, 2, 3)
for i in result:
print(*i)