[자료구조] - 트리(Tree)

💡트리(Tree)의 특징
ㆍ트리는 노드로 이루어진 자료구조이다.
ㆍ트리는 하나의 루트 노드를 갖는다.
ㆍ루트 노드는 0개 이상의 자식노드를 가지고 있다
ㆍ그 자식 노드 또한 0개 이상의 자식노드를 갖고 있다.
ㆍ노드(node)들과 노드를 연결하는 간선(edge)들로 구성되어있다.
ㆍ계층적 구조
ㆍ데이터를 순차적으로 저장하지 않는 비선형 구조

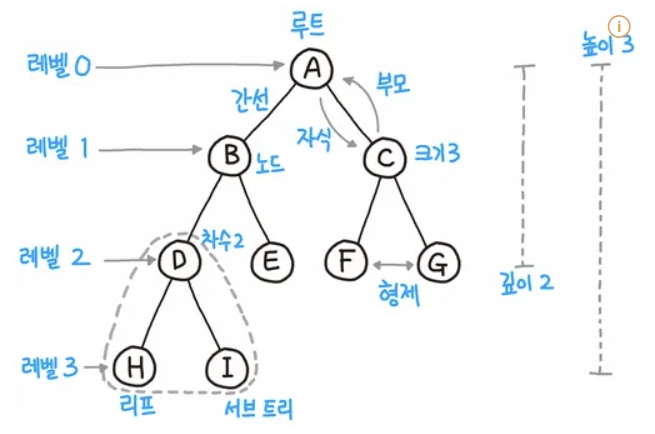
노드(node) : A,B,C,D,E,F,G,H,I 들을 노드라고 한다.
루트 노드(root node/root): 트리에서 부모가 없는 최상위 노드, 트리의 시작점➡️ A
부모 노드(parent node): 루트 노드 방향으로 직접 연결된 노드➡️B의 부모노드는 A
자식 노드(child node): 루트 노드 반대방향으로 직접 연결된 노드
➡️ A의 자식노드는 B
형제 노드(siblings node): 같은 부모 노드를 갖는 노드들 ➡️ B와 C는 형제 노드
차수(degree): 각 노드의 자식의 개수 ➡️ B의 차수는 2
리프 노드(leaf node/leaf): 차수가 0인 정점을 뜻한다. 쉽게 말해 자식이 없는 노드. 단말 노드라 부르기도 한다. ➡️ F, G, H, I
경로(path): 한 노드에서 다른 한 노드에 이르는 길 사이에 있는 노드들의 순서
깊이(depth): 루트 경로의 길이 ➡️ D의 깊이 2, H의 깊이 3
레벨(level): 트리의 특정 깊이를 가지는 노드의 집합 ➡️ 레벨 0: A / 레벨 1: B, C
높이(height): 가장 긴 루트 경로의 길이 ➡️ 3
트리의 차수(degree of tree): 트리의 최대 차수 ➡️ 2
크기(size): 노드의 개수 ➡️ 9

💡트리의 종류
ㆍ이진트리 : 노드가 최대 두 개의 자식 노드를 가지는 트리

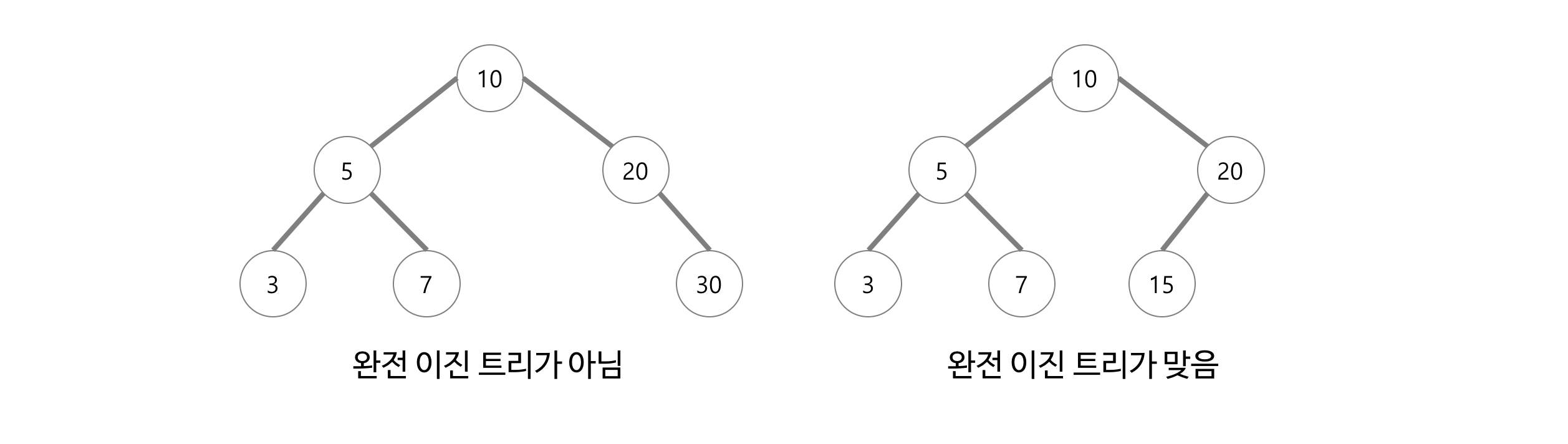
ㆍ완전 이진 트리(Complete Binary Tree): 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있으며, 마지막 레벨은 왼쪽부터 순서대로 채워져 있는 트리

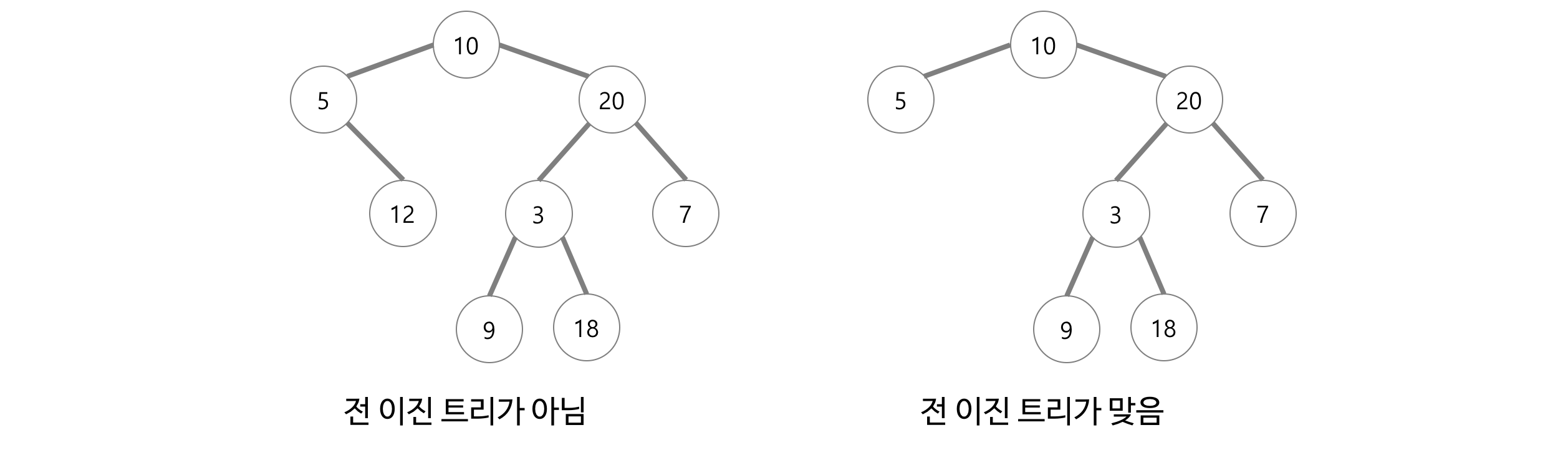
ㆍ 전 이진 트리(Full Binary Tree): 모든 노드가 0개 또는 2개의 자식 노드를 가지는 트리로 1개의 노드를 갖는 트리는 없어야 한다.

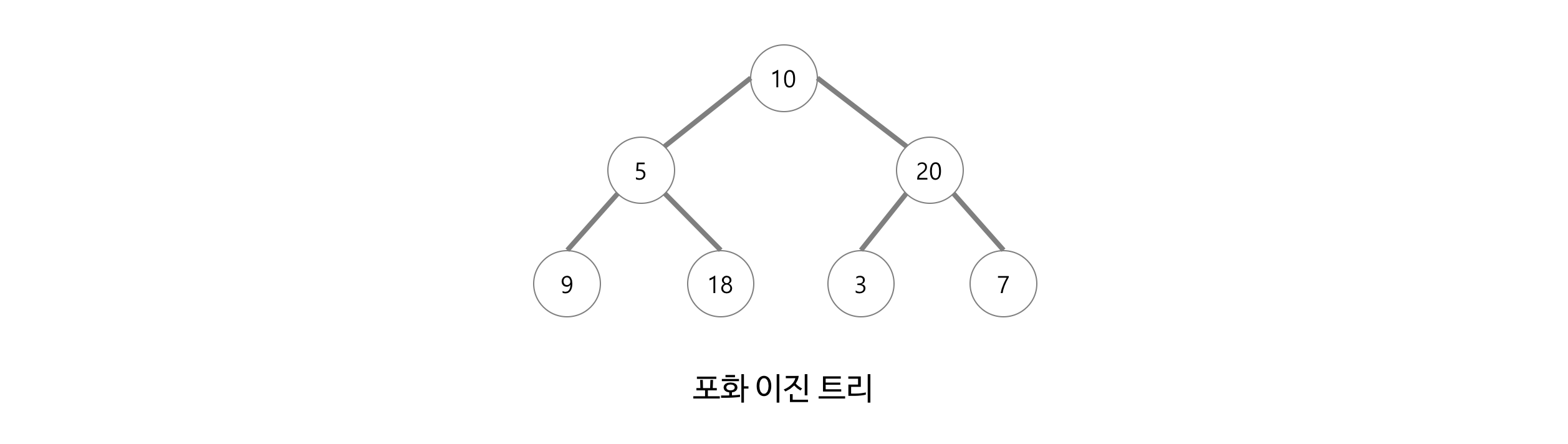
ㆍ포화 이진 트리(Perfect Binary Tree) : 포화 이진트리는 모든 레벨이 (마지막 레벨까지도) 노드로 꽉 차 있는 트리이다.

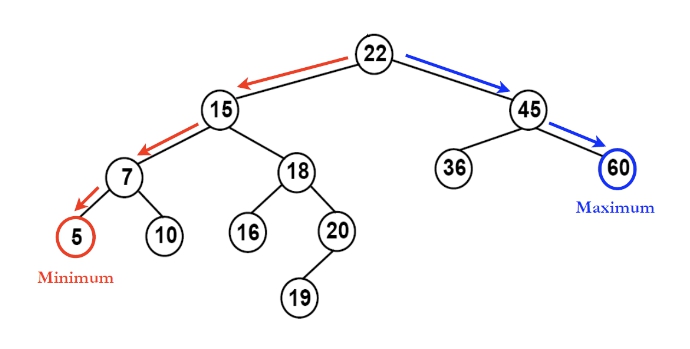
ㆍ이진 탐색 트리 (Binary Search Tree, BST) : 이진 탐색 트리는 이진 트리 기반의 탐색을 위한 자료구조이다.
1. 모든 원소의 키는 유일한 키를 가진다.
2. 왼쪽 서브 트리 키들은 루트 키보다 작다.
3. 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
4. 왼쪽, 오른쪽 서브 트리 모두 이진 탐색 트리이다.

-트리의 순회

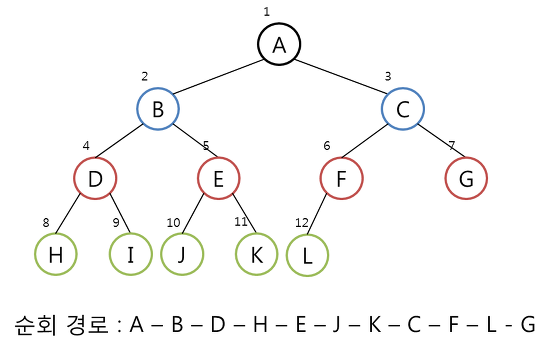
Preorder 운행 (전위 순회) : ROOT -> LEFT -> RIGHT 순

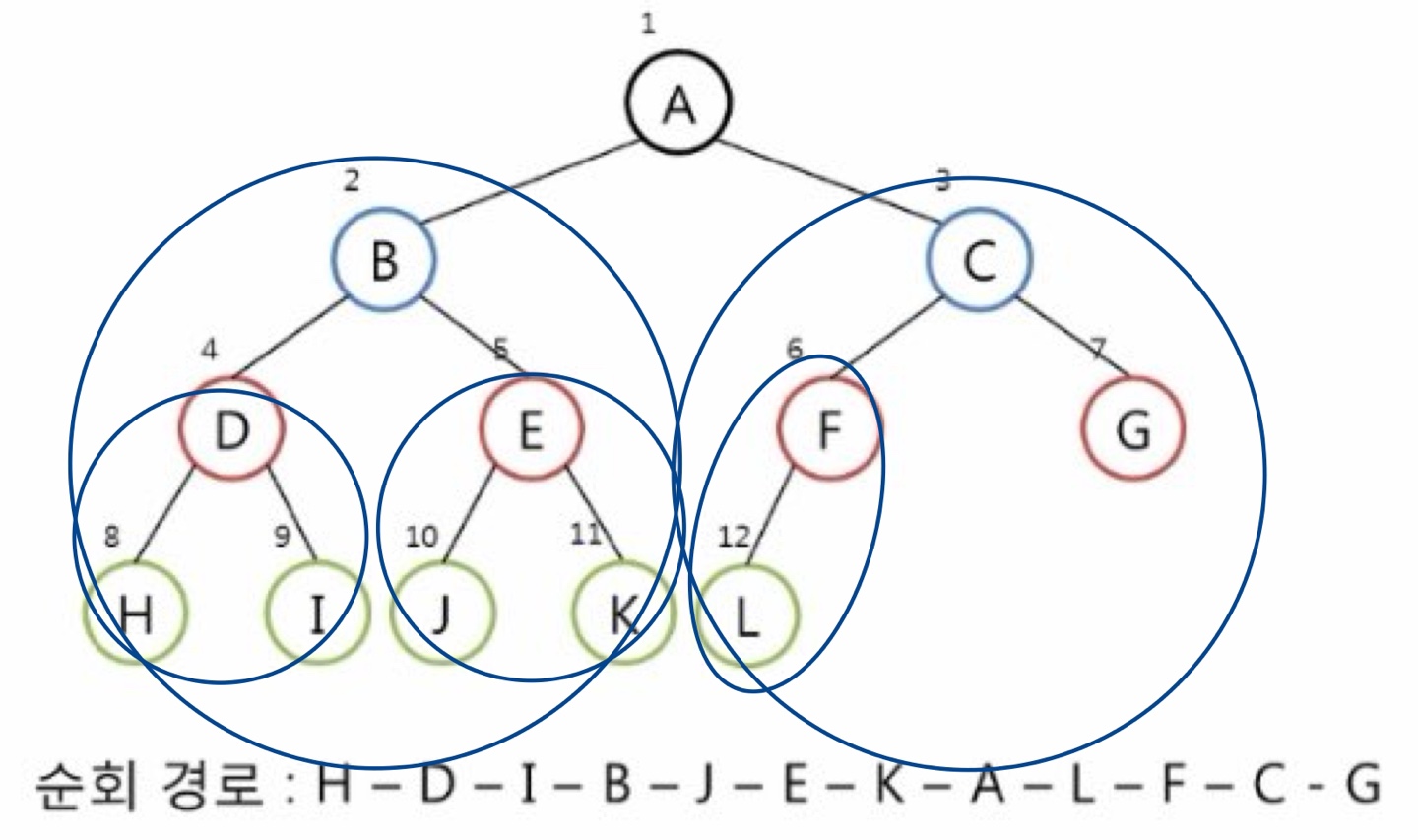
Inorder 운행 (중위 순회) : LEFT -> ROOT -> RIGHT 순
조금 지저분하지만 이렇게 묶음으로 보면 이해하기 쉬웠다..

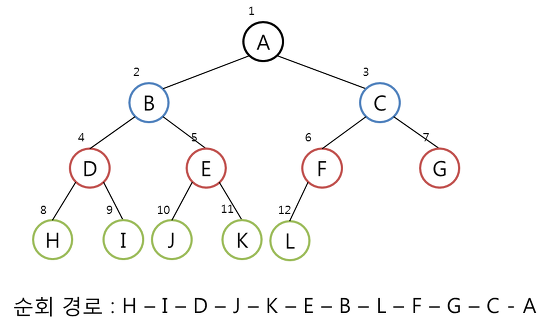
Postorder 운행(후위 순회) : LEFT -> RIGHT -> ROOT 순

💡트리의 용도
컴퓨터의 디렉터리 구조
조직도

💡이진 트리 탐색(Binary Search Tree, BST) 구현 코드
chatgpt의 힘을 빌린...

#include <iostream>
using namespace std;

struct TreeNode { //BST의 노드를 정의하는 구조체
    int key; //노드가 저장하는 데이터 값
    TreeNode *left, *right;
    TreeNode(int val) : key(val), left(nullptr), right(nullptr) {} //자식 노드 포인터는 nullptr로 초기화
};

class BST {
public:
    BST() : root(nullptr) {}  //루트 노드를 nullptr로 초기화

    void insert(int key) { //삽입 함수
        root = insertRec(root, key);
    }

    bool search(int key) { //탐색 함수
        return searchRec(root, key);
    }

    void remove(int key) { //삭제 함수
        root = removeRec(root, key);
    }

    void inorder() { //중위 순회 함수
        inorderRec(root);
        cout << endl;
    }

private:
    TreeNode* root;

    TreeNode* insertRec(TreeNode* node, int key) { 
        if (!node) return new TreeNode(key); 

        //삽입할 키가 현재 노드의 키보다 작으면 왼쪽 서브트리에 삽입
        if (key < node->key) 
            node->left = insertRec(node->left, key); 

        //삽입할 키가 현재 노드의 키보다 크면 오른쪽 서브트리에 삽입
        else if (key > node->key)
            node->right = insertRec(node->right, key);
        return node;
    }

    //탐색 함수
    bool searchRec(TreeNode* node, int key) {
        if (!node) return false;
        if (key == node->key) return true; 
        if (key < node->key)
            return searchRec(node->left, key);
        return searchRec(node->right, key);
    }

    //삭제 함수
    TreeNode* removeRec(TreeNode* node, int key) {
        if (!node) return node;
        if (key < node->key) {
            node->left = removeRec(node->left, key);
        }
        else if (key > node->key) {
            node->right = removeRec(node->right, key);
        }
        else {
            //현재 노드의 왼쪽 자식이 없으면 오른쪽 자식 반환
            if (!node->left) { 
                TreeNode* temp = node->right;
                delete node;
                return temp;
            }

            //현재 노드의 오른쪽 자식이 없으면 왼쪽 자식 반환
            else if (!node->right) {
                TreeNode* temp = node->left;
                delete node;
                return temp;
            }
            TreeNode* temp = minValueNode(node->right);  //오른쪽 서브트리에서 가장 작은 값을 찾는
            node->key = temp->key; // 현재 노드의 키를 오른쪽 서브트리에서 찾은 가장 작은 값으로 변경
            node->right = removeRec(node->right, temp->key); //오른쪽 서브트리에서 가장 작은 값을 삭제
        }
        return node;
    }

    //최소값 노드 찾기 함수
    TreeNode* minValueNode(TreeNode* node) {
        TreeNode* current = node;

        //왼쪽 자식이 nullptr이 아닐 때까지 왼쪽 자식으로 이동하여 가장 왼쪽에 있는 노드를 반환
        while (current && current->left != nullptr) 
            current = current->left; 
        return current; 
    }


    //중위 순회 함수
    void inorderRec(TreeNode* node) {
        if (!node) return; 
        inorderRec(node->left);  //왼쪽 서브트리를 중위 순회
        cout << node->key << " "; 
        inorderRec(node->right); //오른쪽 서브트리를 중위 순회
    }
};

int main() {
    BST tree;
    tree.insert(50);
    tree.insert(30);
    tree.insert(20);
    tree.insert(40);
    tree.insert(70);
    tree.insert(60);
    tree.insert(80);

    cout << "Inorder traversal: "; 
    tree.inorder();

    cout << "Search for 40: " << (tree.search(40) ? "Found" : "Not Found") << endl;
    cout << "Search for 25: " << (tree.search(25) ? "Found" : "Not Found") << endl;

    tree.remove(20); //20 삭제후 중위 순회
    cout << "Inorder traversal after deleting 20: ";
    tree.inorder();

    tree.remove(30);
    cout << "Inorder traversal after deleting 30: ";
    tree.inorder();

    tree.remove(50);
    cout << "Inorder traversal after deleting 50: ";
    tree.inorder();

    return 0;
}

💡출력

Inorder traversal: 20 30 40 50 60 70 80
Search for 40: Found
Search for 25: Not Found
Inorder traversal after deleting 20: 30 40 50 60 70 80
Inorder traversal after deleting 30: 40 50 60 70 80
Inorder traversal after deleting 50: 40 60 70 80