동적 프로그래밍(Dynamic Programming)

• 최근 취업 준비를 하면서 알고리즘을 공부 중인데, 알고리즘 공부방법이 최근까지 잘못됬다는걸 깨닫고 공부 방법을 바꿔보려고 한다. 유형을 먼져 공부하고 해당 유형에 맞는 문제들을 20문제 정도 풀어보니 Velog 에 글을 쓰며 설명할 정도로는 이해한 것 같아 적어보려고 한다.

• 동적 프로그래밍의 기본 개념은 반복되는 프로세스 를 찾는 것이 중점이라고 생각한다.

• 많이 풀어보면서 느낀건(물론, 아직도 더풀어야 하지만) 반복되는 프로세스를 찾았을때, 점화식을 세워 동적프로그래밍의 장점인 반복되는 프로세스의 메모리에 저장하여 빠르게 값을 저장하여, 효율성을 높이는 것이다. 일단 백문이 불여일견이라고 코드로 보여주겠다.

• 아래가 동적 프로그래밍으로 설계한 Fibonacci 코드이다.
  

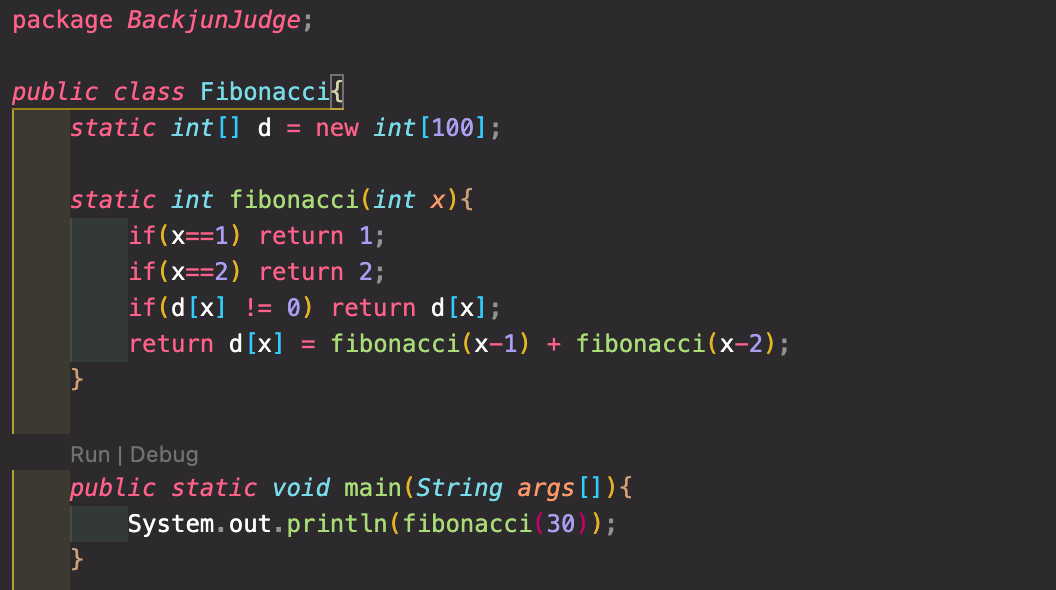
• 아래가 기존 재귀로 호출한 코드이다.
  

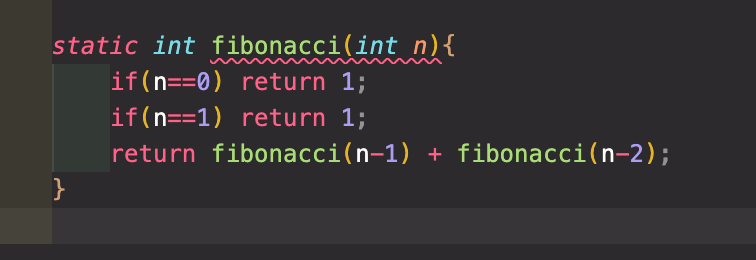
• 자 Fibonacci 함수에 50 을 넣어보자! 그럼 왜 빠른가? Fibonacci 로 두번째 기존 재귀로 호출하게 되면 호출될때 마다 연산과정을 진행하므로 시간이 걸린다. 근데 dp 배열을 이용하게 되면, 기존에 연산 했던 과정의 값들은 저장되어 있기에 연산 과정을 진행하지 않고, 해당 값만 호출하여 이용한다! 즉, 연산과정이 없어진다는 것이다.

• 자 근데, 사실 나도 다른 블로그를 보면서 여기까지 보더라도 잘 이해를 못했다. 그러니 내가 푼 문제들 한가지를 골라서, 보여주겠다.

백준 알고리즘 2156번 - 포도주 시식

• 문제는 간단히 설명하면, 포도주들의 양을 입력하고, 포도주는 연속되어 3개를 먹을수 없습니다.(즉 2개까지) 해당 방식으로 제일 최대로 먹을 수 있는 방법을 찾는 것입니다.

• 그러면 연속해서 먹을 수 없으므로 패턴은 3개로 획일화 됩니다.
  먹는다 : YES , 안먹는다 : NO

• YYN
• NYY
• YNY

• 자 동적 프로그래밍은 이런 일종의 반복되는 패턴을 찾아내는 것이 중요하다. 그렇담 우리가 이걸 어떻게 설계 해야 하나? 지금 저 패턴 중 제일 큰값을 계속해서 넣어 주기만 하면 된다.

• dp[0] 은 Input[0] 으로 지정해준다.

• dp[1] 은 Input[1] 으로 지정해준다.

• dp[2] 는 Math.max(dp[1]. Math.max(array[0] + array[2] , array[1] + array[2])) 로 지정한다. 위의 패턴을 그대로 적어 일단 3번째 까지는 구한것이다.

• 이제 3번째부터 위의 식을 그대로 N 으로 바꿔준다

• dp[N] = Math.max(dp[N-1]. Math.max(dp[N-2] + array[i] , dp[N-3] + array[N-1] + array[N])); 이제 설계한 식대로 풀기만 하면 답이 나온다.

public class Back2156 {
    
    static int[] dp;
    static int[] array;
    static int N;
    
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        N = scan.nextInt();
        dp = new int[N];
        array = new int[N];
        for(int i = 0; i<N; i++){
            array[i] = scan.nextInt();
        }
        if(N >= 1){         
            dp[0] = array[0];
        }
        if(N >= 2){
            dp[1] = dp[0] +array[1];
        }
        if(N >= 3){
            dp[2] = Math.max(dp[1], Math.max(array[0]+array[2] , array[1]+array[2]));
        }
        for(int i = 3; i<N; i++){
            dp[i] = Math.max(dp[i-1], Math.max(dp[i-2] + array[i] , dp[i-3] + array[i-1] + array[i]));
        }
        System.out.println(dp[N-1]);
        scan.close();
    }
}

최대한 이해할 수 있는 문제로 풀어봤는데, 이해가 안간다면 해당 방식으로 프로세스를 최적화하고 쉬운 문제들 부터 풀어보길 바란다.