KL-Divergence에 대하여

안녕하세요. 오늘은 여러 논문들에서 자주 등장하는 개념인 KL-Divergence에 대해서 정리해보고자 합니다.

두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다. (위키피디아)

KL-Divergence의 정의

• 결합확률분포의 정보량($H(p,q)$)와 단일확률분포의 정보량($H(P)$)의 차이를 의미합니다.
  $KL(p||q) = H(p,q) - H(p) = \sum_i p_i log{p_i \over q_i}$
  • 증명 $H(P,Q)-H(P) = (- \sum_i p_i log q_i) - (- \sum_x p_i log p_i)$
    

KL-Divergence의 특성

1. $KL(p||q)≥0$
   

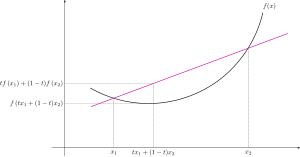
   이 특성을 알기 위해서는 Jensen 부등식의 개념을 알아야 합니다. Jensen 부등식이란 아래로 볼록한 그래프(convex function)에서는 임의의 두 $x_1,x_2$에 대하여 아래와 같은 부등식이 성립한다는 것 입니다.

   $f(t(x_1)+(1-t)(x_2) \le t(f(x_1)) + (1-t)(f(x_2))$

   그래프를 통해 이해하면 $x_1, x_2$ 사이의 $f(x)$ 상의 어떠한 점이라도 $f(x_1),f(x_2)$ 을 잇는 직선 보다 작기 때문에 위와 같은 부등식으로 표현할 수 있습니다. 이를 확률적으로 표현하면 아래와 같이 정의할 수 있습니다.

   $f(E[X]) \le E[f(X)]$

   KL-Divergence 식에서 log 함수를 음수화하여 $f(x)=-log$ 라고 하면 $f(x)$는 위의 Jensen 부등식이 만족하는 convex function이 됩니다. 위의 부등식에 $x={q_i \over p_i}$ 를 대입하면,

   $KL-D =- \int p(x) log {q(x)\over p(x)}dx \ge -log \int p(x){q(x)\over p(x)}dx = -log \int q(x)dx = -log 1 = 0$

   이므로 KL-Divergence $\ge$ 0 이 성립합니다.
   

2. $KL(p|q) ≠ KL(q|p)$

   • KL-Divergence는 거리 개념이 아니라는 것을 의미
   • KL-Divergence를 평균내어 거리 개념으로 응용한 것이 Jensin-Shannon divergence
     $JSD(p||q) = {1 \over 2}KL(p||M) + {1\over2}KL(q||M)$

KL-Divergence와 log-likelihood

KL-Divergence는 Diffusion 논문을 읽으면 많이 접할 수 있는 논문입니다. 이미지를 생성할 때 이미지의 확률분포 $p(x)$를 유추하기 위해 파라미터 $\theta$를 활용해 $q(x|\theta)$ 로 확률분포를 근사하고자 합니다. $\theta$ 를 찾는 과정에서 $p(x)$ 와 $q(x|\theta)$ 사이의 KL-Divergence를 최소화하는 방향으로 모델을 학습합니다.
물론 우리는 확률 분포 $p(x)$를 알지 못하기 때문에 직접적인 학습은 불가능하지만 $p(x)$으로부터의 샘플데이터인 training set이 있기 때문에 이 표본집단을 이용해서 대신 학습할 순 있습니다.

여기서 $-\ln q(x_n|\theta)$가 근사하고자 하는 확률분포 $q(x|\theta)$의 negative log-likelihood 이고, KL-Divergence를 최대화하기 위해서는 log-likelihood를 최대화 해야한다는 것을 알 수 있습니다.