[알고리즘] 백준 1003번 문제 풀이

안녕하세요! 오늘은 알고리즘 공부를 하다가 새로운 개념을 알게되어 정리하고자 글을 쓰게 되었습니다.

백준 1003번 문제는 아래와 같습니다.

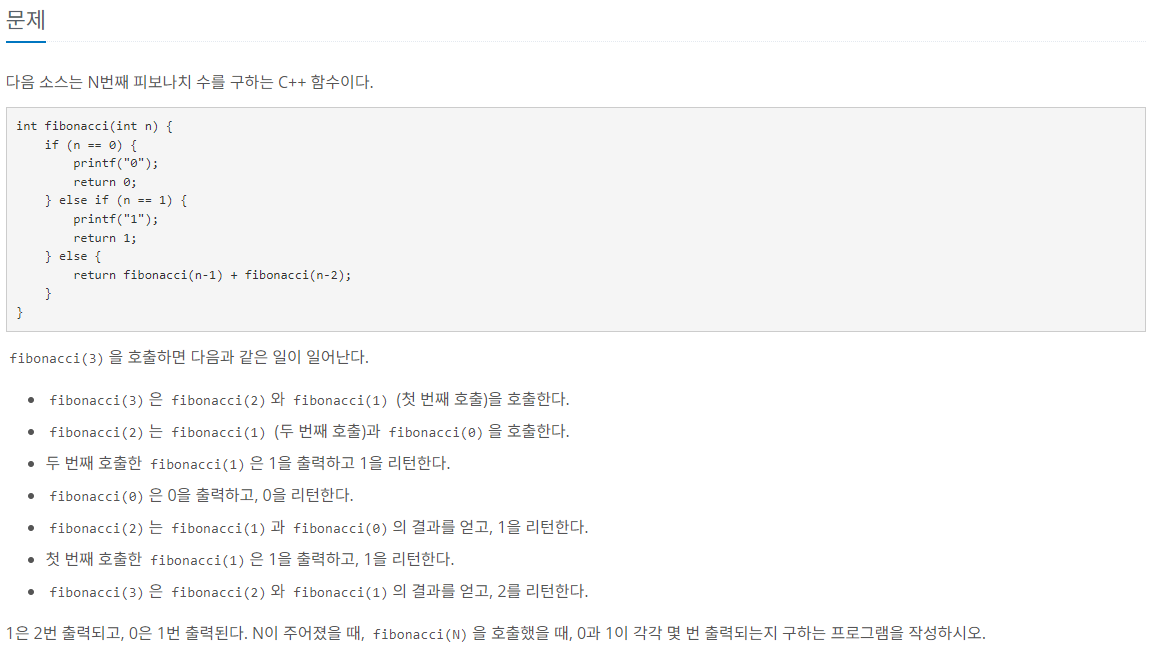
사실 문제를 이해하는데도 꽤 오랜 시간이 걸렸는데, 결국 피보나치 수열의 결과에서 0과 1이 몇번 출력되는지 횟수를 다 더하면 되는 것이었습니다.

개념 설명

일단 피보나치 수열이라는 말을 들은지가 꽤 되었던지라 문제의 C++ 함수대로 파이썬 함수를 만들어 돌려보았습니다.

def fibonacci(n: int):
    if n==0:
        print('0')
        return 0
    elif n==1:
        print('1')
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

실행결과

fibonacci(3)
>>>1
>>>0
>>>1

fibonacci(4)
>>>1
>>>0
>>>1
>>>1
>>>0

이렇게 출력됩니다. 눈치채셨다시피 fibonacci(4)의 결과는 fibonacci(3)과 fibonacci(2)의 결과를 이어서 출력하는 것과 같습니다.

저는 처음에는 이 피보나치 수열 함수를 그대로 활용해서 0과 1이 반환되는 횟수만 dictionary에 저장해 출력하도록 했습니다. 그러나, fibonacci(40)이 입력으로 들어오는 순간 시간초과가 발생했습니다. 아무래도 동일한 피보나치 연산이 연쇄적으로 일어나다보니 시간이 오래걸릴 수 밖에 없을 것 같습니다.

동적 계획법

이를 해결하기 위해 구글링을 해보니 피보나치 수열을 빠른 속도로 계산하기 위해서는 D.P 라는 동적계획법을 활용해서 풀면 된다고 합니다.

동적 계획법이란
1) 알고리즘은 메모리 공간을 약간 더 사용하면서 연산 속도를 비약적으로 증가시킬 수 있는 기법
2) 한번 계산된 값은 메모리에 저장시켜 반복된 연산이 일어나지 않도록 한다.

위의 개념을 활용해서 재귀 연산을 활용하는 Top-Down 방식의 DP와 반복문을 활용하는 Down-Up 방식의 DP가 있습니다.

저는 오늘 조금 더 직관적인 Top-Down 방식의 DP 연산을 활용해 이 문제를 풀었습니다.
동적 계획법을 활용할 때는 위의 2)번을 잘 생각해야합니다. 피보나치 수열의 연산에서 어느 부분이 반복적으로 연산되는 걸까요?

예를 들어 fibonacci(40)을 계산한다고 했을 때 fibonacci(39) + fibonacci(38) 이 계산되야 합니다. 그럼 fibonacci(39)는 fibonacci(38) + fibonacci(37)이 되고, fibonacci(38)은 fibonacci(37) + fibonacci(36)이 됩니다.
즉, fibonacci(40) = fibonacci(38) + fibonacci(37) + fibonacci(37) + fibonacci(36) 이 됩니다. 벌써 fibonacci(37)이 2번 계산되어야함을 알 수 있습니다.

이런 점을 활용해서 한번 계산된 fibonacci 함수는 메모리에 저장해 반복 연산되지 않고 필요할 때마다 불러오면 빠른 연산이 가능합니다.

문제 풀이

0과 1이 출력되는 횟수를 계산함으로 저는 0이 나오는 횟수를 저장할 리스트와, 1이 나오는 횟수를 저장할 리스트를 만들었습니다. 또한 n이 최대 40이기 때문에 각 리스트의 길이는 40으로 지정해줍니다.

그리고 각 리스트의 0과 1의 갯수는 피보나치 계산법과 동일하게 이전 두 피보나치 연산 값의 0과 1의 갯수를 더한 것과 동일하게 만들어주고, 한번 계산된 피보나치 연산은 다시 연산되지 않고 저장된 값에서 불러오게 합니다.

저의 풀이는 아래와 같습니다.

import sys

num = int(sys.stdin.readline())

def fibonacci(n: int):
    if n == 0:
        count0[n]=1
        return count0, count1
    elif n == 1:
        count1[n]=1
        return count0, count1

    elif count0[n] != 0 or count1[n] != 0:
        return count0, count1
    else:
        count0[n] = fibonacci(n-1)[0][n-1] + fibonacci(n-2)[0][n-2]
        count1[n] = fibonacci(n-1)[1][n-1] + fibonacci(n-2)[1][n-2]
        return count0, count1

for i in range(num):
    count0=[0]*(40+1)
    count1=[0]*(40+1)
    q = int(sys.stdin.readline())
    print(fibonacci(q)[0][q],fibonacci(q)[1][q])

저의 풀이가 완벽하지는 않겠지만 D.P의 개념을 정확하게 활용해보고자 했습니다. 혹시 문제 해결 과정에서 오류가 있거나, 더 좋은 방법이 있다면 댓글을 통해 알려주시면 감사하겠습니다.

좋은 연말 보내세요!

Reference
DP(동적계획법) 설명: https://devvvyang.tistory.com/15
백준 풀이: https://edder773.tistory.com/64